 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Методические рекомендации по решению задач 12
Для получения наиболее простых уравнений равновесия (если это не усложняет ход решения в остальном) следует одну из координатных осей проводить перпендикулярно возможно большему числу неизвестных сил, а за центр моментов брать точку, в которой пересекается возможно большее число неизвестных сил. При вычислении момента силы удобно иногда разлагать данную силу на составляющие и пользоваться теоремой о моменте равнодействующей (теоремой Вариньона). Если на тело наряду с силами действуют и пары, лежащие в плоскости сил, то при составлении уравнений равновесия в уравнения проекций пары не войдут, так как сумма проекций сил пары на любую ось равна нулю. В уравнениях же моментов к моментам сил алгебраически прибавятся моменты пар, так как сумма моментов сил пары относительно любого центра равна моменту пары. Примеры решения задач Пример 1. Найти реакции опор конструкции при следующих данных: G = 40 кН; Р = 5 кН; М = 10 кНм; q = 2,5 кН/м; а = 30°; размеры - в м.
Покажем также реакцию Для плоской системы сил, приложенных к балке, составляем три уравнения равновесия:
Из уравнения (1) получаем Из уравнения (2)
Из уравнения (3)
Значения
Пример 2. Однородная гладкая балка АВ силой тяжести Р = 2 кН, закрепленная в точке А при помощи шарнира, опирается в точке С на стену. В точке В подвешен груз Q = 1 кН. Определить опорные реакции в точках А и С, если балка составляет с горизонтом угол а = 30°, h = 1 м, и
отсюда находим
Решение. Заменяя действие опор реакциями, составляем силовую схему. Уравнения равновесия возьмем в форме трех моментов. В качестве точек, относительно которых составляются уравнения моментов, выберем точки А, В и С. Уравнения равновесия при этом будут
отсюда находим
Пример 4. К балке приложены сосредоточенная сила F= 16 кН и равномерно распределенная нагрузка интенсивности q = 1,2 кН/м. Угол а = 30°, а = 3 м, b=7 м,
Решение. Действие опор на балку заменяем реакциями Уравнения равновесия имеют вид
Решая эти уравнения, получаем
Пример 5. К однородной балке, сила тяжести которой Q и длина
Решение. Силовая схема изображена на рис. Уравнения равновесия будут
отсюда имеем
12 |



 Решение. Рассмотрим систему сил, приложенных к балке АВ. Отбрасываем связи: шарнирно неподвижную опору А, стержень CD и нить.
Решение. Рассмотрим систему сил, приложенных к балке АВ. Отбрасываем связи: шарнирно неподвижную опору А, стержень CD и нить. Действие связей заменяем их реакциями. Так как направление реакции шарнирно-неподвижной опоры А неизвестно, то определяем ее составляющие
Действие связей заменяем их реакциями. Так как направление реакции шарнирно-неподвижной опоры А неизвестно, то определяем ее составляющие  .
. стержня CD и реакцию S нити. Модуль этой реакции равен Р. Равномерно распределенную нагрузку интенсивностью q заменяем сосредоточенной силой Q, равной Q = 5 кН и приложенной в центре тяжести эпюры этой нагрузки.
стержня CD и реакцию S нити. Модуль этой реакции равен Р. Равномерно распределенную нагрузку интенсивностью q заменяем сосредоточенной силой Q, равной Q = 5 кН и приложенной в центре тяжести эпюры этой нагрузки. (1)
(1) (2)
(2) (3)
(3)
 ;
;
 получаются положительными. Это указывает на то, что принятые направления этих сил совпадают с их действительными направлениями.
получаются положительными. Это указывает на то, что принятые направления этих сил совпадают с их действительными направлениями. = 3 м.
= 3 м. Решение. Образуем силовую схему, заменив действие связей их реакциями. Реакция в точке А не известна ни по величине, ни по направлению, поэтому будем искать эту реакцию через ее проекции
Решение. Образуем силовую схему, заменив действие связей их реакциями. Реакция в точке А не известна ни по величине, ни по направлению, поэтому будем искать эту реакцию через ее проекции 

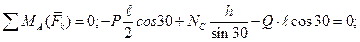

 ;
;
 Пример 3. Ферма опирается на неподвижный шарнир А и каток В, который может без трения перемещаться по наклонной плоскости. Определить реакции опор А и В, если к ферме приложены силы Р = 30 кН и P1 = 60 кН.
Пример 3. Ферма опирается на неподвижный шарнир А и каток В, который может без трения перемещаться по наклонной плоскости. Определить реакции опор А и В, если к ферме приложены силы Р = 30 кН и P1 = 60 кН.
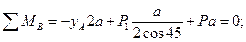

 ;
; 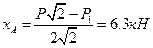

 = 12 м. Сила тяжести Р = 5 кН. Определить реакции опор.
= 12 м. Сила тяжести Р = 5 кН. Определить реакции опор.
 , а распределенную нагрузку - ее равнодействующей
, а распределенную нагрузку - ее равнодействующей  , приложенной в середине отрезка DB.
, приложенной в середине отрезка DB.

 ;
; ,
, ;
;




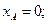
 ;
;