 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Момент этой пары численно равен моменту исходной силы относительно центра приведения. 12
Лекция 3 Плоская произвольная система сил - силы лежат в одной плоскости и их линии действия не пересекаются в одной точке. Для рассмотрения такой системы сил необходимо ввести новые понятия: 1. Момент силы относительно точки на плоскости. 2. Пара сил. Момент пары сил.
Момент силы относительно точки на плоскости - алгебраическая величина, равная произведению модуля силы на плечо, взятая со знаком + (плюс), если вращение плоскости под действием силы происходит против часовой стрелки, и со знаком - (минус) в противном случае. Плечо силы - длина перпендикуляра, опущенного из точки на линию действия силы
Пара сил - совокупность двух параллельных друг другу сил, равных по величине и направленных в противоположные стороны. Пара сил более не может быть упрощена (не может быть заменена одной силой) и представляет собой новую силовую характеристику механического взаимодействия.
Момент пары сил на плоскости (теорема о моменте пары сил) - не зависит от выбора центра приведения (полюса) и равен произведению модуля любой из сил пары на плечо пары, взятым со знаком + (плюс), если вращение плоскости под действием пары сил происходит против часовой стрелки, и со знаком - (минус) в противном случае. Плечо пары сил - длина перпендикуляра, опущенного из любой точки на линии действия одной из сил пары на линию действия другой силы этой пары. В независимости момента пары от выбора полюса можно убедиться вычислением суммы моментов от каждой из сил относительно любого центра.
Теоремы о парах: (Теоремы приводятся без доказательств). О переносе пары сил в плоскости ее действия - Пару сил можно перенести в любое место в плоскости ее действия. Кинематическое состояние тела не изменится. Об эквивалентности пар сил - Пару сил можно заменить другой парой сил, если их моменты алгебраически равны. Кинематическое состояние тела не изменится.
О сложении пар сил на плоскости - Систему пар сил на плоскости можно заменить одной парой, момент которой равен алгебраической сумме моментов исходных пар. Кинематическое состояние тела не изменится. Условие равновесия системы пар сил - Приведение силы к заданному центру (метод Пуансо) - силу можно перенести параллельно самой себе в любую точку плоскости, если добавить соответствующую пару сил, момент которой равен моменту этой силы относительно рассматриваемой точки.
Добавим к системе в точке А две силы, равные по величине между собой и величине заданной силы, направленные по одной прямой в противоположные стороны и параллельные заданной силе: Кинематическое состояние не изменилось (аксиома о присоединении). Исходная сила и одна из добавленных сил противоположно направленная образуют пару сил. Момент этой пары численно равен моменту исходной силы относительно центра приведения.
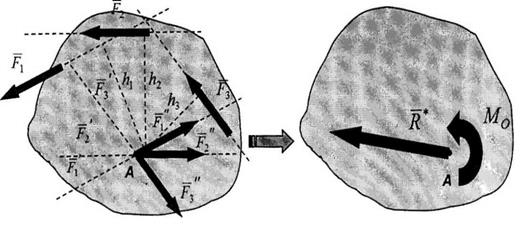
Во многих случаях пару сил удобно изображать дуговой стрелкой. Приведение плоской произвольной системы сил к заданному центру - выбираем произвольную точку на плоскости и каждую из сил переносим по методу Пуансо в эту точку. Вместо исходной произвольной системы получим сходящуюся систему сил и систему пар.
Сходящиеся система сил приводится к одной силе, приложенной в центре приведения, которая ранее называлась равнодействующей, но теперь эта сила не заменяет исходную систему сил, поскольку после приведения возникла система пар. Система пар приводится к одной паре (теорема о сложении пар), момент которой равен алгебраической сумме моментов исходных сил относительно центра приведения. В общем случае плоская произвольная система сил приводится к одной силе, называемой главным вектором и паре с моментом, равным главному моменту всех сил системы относительно центра приведения:
Условием равновесия плоской произвольной системы силявляется одновременное обращение главного вектора и главного момента системы в ноль:
Условия равновесия (Iформа) получаются в виде системы трёх уравнений из условий равновесия с использованием выражений для проекций главного вектора: Существуют ещё две формы уравнений равновесия (II и III формы):
Следует обратить внимание на то, что II и III формы уравнений равновесия имеют ограничения, связанные с выбором одной из осей, например, х, и точки С относительно положения точек А и В. Ограничения, накладываемые на выбор оси х (не перпендикулярно АВ)
Если все силы, расположенные в плоскости, взаимно параллельны, то число уравнений равновесия сократится до двух. Эти уравнения можно записать в одной из двух форм:
где ось у параллельна силам;
при этом отрезок АВ, соединяющий центры моментов А и В, не должен быть параллелен силам.
Теорема Вариньона о моменте равнодействующей - Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра равен алгебраической сумме моментов сил системы относительно того же центра.
Доказательство: Пусть система сил Такая система не находится в равновесии Таким образом, система исходных сил Примеры использования теоремы о моменте равнодействующей: 1. Определение момента силы относительно точки, когда сложно вычислять плечо силы. Например:
Силу F разложим на составляющие
2. Доказательство необходимости ограничений для II и III форм уравнений равновесия:
12 |
- главный вектор
- главный момент
, гарантируют, что ни одно из уравнений не обращается в тождество, при выполнении двух других уравнений.
,
приводится к равнодействующей, приложенной в точке О.
. Уравновесим эту систему силой R', равной равнодействующей R, направленной по линии ее действия в противоположную сторону (аксиома о двух силах).
и уравновешивающей силы R' находится в равновесии и должна удовлетворять уравнениям равновесия, например: 
. Поскольку сила R', равна равнодействующей R и направлена по линии ее действия в противоположную сторону, то 
. Подстановка этого равенства в уравнение равновесия дает: 
или 
. Тогда момент силы F относительно точки А можно вычислить как сумму моментов каждой из сил относительно этой точки:
, то система приводится к равнодействующей, при этом она проходит через точку А так как её момент относительно этой точки должен быть равен нулю. Если при этом 
, то равнодействующая должна проходить через точку В. Тогда проекция равнодействующей на ось, перпендикулярную АВ, и момент равнодействующей относительно точки, лежащей на АВ, будут тождественно равны нулю при любом значении равнодействующей.