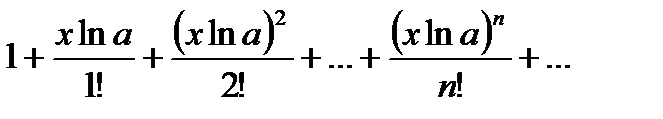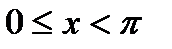 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ИТЕРАЦИОННЫЕ ЦИКЛЫ. ВЫЧИСЛЕНИЕ СУММЫ БЕСКОНЕЧНОГО РЯДА
Подготовка к работе По указанной литературе и методическим указаниям к данной работе изучить порядок работы. Ответить на контрольные вопросы. 2.2. Контрольные вопросы 1. Что такое итерационный цикл? С помощью каких операторов организуется? 2. Какие ограничения налагаются на использование управляющей переменной (параметра цикла) в цикле for? 3. В каких случаях предпочтительнее использовать для организации циклов оператор for? Что записывается в заголовке этого оператора? 4. Что представляет собой составной оператор? Как ограничиваются операторы, объединённые в составной оператор? 5. Что такое рекуррентная формула? Правило записи рекуррентной формулы. 6. Что такое вложенные циклы? Какие дополнительные условия необходимо соблюдать при организации вложенных циклов? 7. В чём отличия операторов повтора while и repeat? Задание для индивидуальной работы Разработать алгоритм и программу, определяющие сумму ряда с заданной погрешностью
Пример выполнения задания Рассмотрим задачу вычисления функции y=cos(x) с погрешностью
Накопление суммы производим по рекуррентной формуле Sn=Sn-1+tn(x) Текущий член ряда будем вычислять по формуле
На рис. 2.1 приведён алгоритм вычисления бесконечного ряда с заданной погрешностью eps.
Рис. 2.1. Алгоритм вычисления суммы бесконечного ряда
Программа вычисления суммы имеет следующий вид: {Цель: вычисление суммы с заданной погрешностью по } { итерационному алгоритму } {Переменные:x-аргумент функции,S-сумма } { eps-погрешность вычисления суммы } { n-переменная суммирования } { t- слагаемое }
program symma; var eps,S,t,x:real; n:integer; Begin {ввод исходных данных} Writeln('введите x, погрешность eps'); Read(x,eps); Writeln('для x= ',x:6:2,' с погрешностью ',eps:6:4); t:=1; S:=1; n:=1; while abs(t)>eps do {начало цикла} begin t:=-t*x*x/(2*n*(2*n-1)); S:=S+t; n:=n+1; end; {конец цикла} Writeln('n= ',n,'S= ',S:7:4); Writeln('контрольное значение = ',cos(x):7:4); end. ОБРАБОТКА ОДНОМЕРНЫХ МАССИВОВ ДАННЫХ Подготовка к работе По указанной литературе и методическим указаниям к данной работе изучить порядок работы. Ответить на контрольные вопросы. 3.2. Контрольные вопросы 1. Что такое массив? 2. Как определить местоположение элемента в массиве? 3. Что такое индекс? Каким требованиям он должен удовлетворять? 4. Особенности расположения элементов массива в памяти ЭВМ. Особенности расположения в памяти элементов многомерных массивов. 5. Общие и отличительные черты одномерных, двумерных и n-мерных массивов. 6. В каких операциях могут участвовать массивы и какие к ним предъявляются требования? 7. Каким образом в Паскале задаётся обращение к элементу массива? 8. Что называется инициализацией массива, и зачем она применяется? 9. Что называется сортировкой массива? Какие методы сортировки вы знаете. 10. Что вы понимаете под поиском элемента в массиве? 11. Что называется главной (побочной) диагональю матрицы? Что такое транспонирование матрицы? |
(ипсилон) для произвольно заданного аргумента x. Определить число повторений итерационного цикла.
