ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Сбор и регистрация исходных статистических данных 12
Аннотация Беляева А.В. «Статистическая обработка результатов выборочного контроля по количественному признаку», Курсовая работа по дисциплине «Статистические методы управления качеством». – Новокузнецк, 2013. – ?? с., Табл. 7, ил. 2, источников ??. Выполнена статистическая обработка результатов выборочного контроля скрепок. Объем выборки составил 150 штук. В качестве параметра качества выбрана длина скрепок. Измерения производились штангенциркулем с ценой деления 0,1 мм. Результаты измерений представлены в виде упорядоченного и интервального рядов. Рассчитаны характеристики положения (средняя арифметическая) и рассеяния (дисперсия, стандартное отклонение и размах). Построенная по результатам измерения гистограмма имеет один четко выраженный пик, свойственный для обычного процесса. Выдвинутая гипотеза о нормальном распределении в ходе ее проверки при помощи критерия Пирсона была отвергнута, т.е. распределение случайных величин в генеральной совокупности подчиняется нормальному закону распределения. Анализ контрольных карт выборочных средних и размахов показал отсутствие точек, вышедших за контрольные границы и особых, маловероятных структур точек согласно ГОСТ 50779.42-99 (ИСО 8258-91). Это говорит о том, что на исследуемый процесс производства заклепок действуют только обычные, случайные причины, он статистически стабилен, т.е. находится в состоянии статистической управляемости.
Исполнитель _________ Беляева А.В. Содержание Введение........................................................................................................... 4 1. Сбор и регистрация исходных статистических данных............................ 6 2. Расчет числовых характеристик экспериментальных данных.................. 9 3. Графическое распределение статистических данных.............................. 12 Проверка согласия опытного распределения с теоретическим нормальным.................................................................................................. 13 5. Построение и анализ контрольных карт средних арифметических и размахов.............................................................................................................................................................................. 16 Заключение................................................................................................... .21 Список использованной литературы............................................................ 22 Введение Статистические методы (методы, основанные на использовании математической статистики), являются эффективным инструментом сбора и анализа информации о качестве. Применение этих методов, не требует больших затрат и позволяет с заданной степенью точности и достоверностью судить о состоянии исследуемых явлений (объектов, процессов) в системе качества, прогнозировать и регулировать проблемы на всех этапах жизненного цикла продукции и на основе этого вырабатывать оптимальные управленческие решения. Статистические методы контроля производства и качества продукции имеют ряд преимуществ перед другими методами: - являются профилактическими; - позволяют во многих случаях обоснованно перейти к выборочному контролю и тем самым снизить трудоемкость контрольных операций; - создают условия для наглядного изображения динамики изменения качества продукции и настроенности процесса производства, что позволяет своевременно принимать меры к предупреждению брака не только контролерам, но и работникам цеха – рабочим, бригадирам, технологам, наладчикам, мастерам. Наиболее распространенными методами статистического анализа точности технологических процессов являются: - сравнение средних значений параметров с номинальными; - сравнение дисперсий; - оценка коэффициентов корреляции; - регрессионный анализ и др. Для успешного применения статистических методов контроля качества продукции необходимы соответствующие руководства и стандарты, доступные широкому кругу инженерно-технических работников. Стандарты на статистический приемочный контроль обеспечивают возможность объективно сравнивать уровни качества партий однотипной продукции, как во времени, так и по различным предприятиям. Цель работы - приобретение практических навыков по организации выборочного контроля качества и обработки его результатов. Задачи: 1) произвести выборку объемом n; 2) выполнить расчет числовых характеристик экспериментальных данных; 3) построить графическое представление статистических данных в виде гистограммы, проанализировать полученное распределение; 4) выполнить проверку гипотезы о том, что контролируемый показатель качества всей партии, из которой сделана исследуемая выборка, характеризуется нормальным распределением при 5) построить и проанализировать контрольные карты средних арифметических и размахов. Сбор и регистрация исходных статистических данных Была взята выборка, состоящая из 150 скрепок, и измерена длина каждой. В таблице 1 представлена последовательность появления значений. Таблица 1 –Измеренные значения длин скрепок
Продолжение таблицы 1
При большом объеме выборки совокупность измеренных параметров представляют в виде упорядоченного, либо в виде интервального статистических рядов. Полученные результаты измерений представляем в виде упорядоченного статистического ряда. Упорядоченный статистический ряд - таблица, в которой измеренные значения ранжированы в возрастающем или убывающем порядке и для каждого повторяющегося значения Xi подсчитано число повторений hi. 150 измерений преобразованы в упорядоченный ряд, который представлен в таблице 2. Таблица 2 - Упорядоченный ряд наблюдений, составленный по результатам измерений
Продолжение таблицы 2
Для упрощения анализа и дальнейшей математической обработки измеренных значений целесообразнее представить в виде интервального статистического ряда, в таблице 3, где в качестве первого приближения для определения интервалов k можно использовать формулу (1):
где n − объем выборки. В данном случае, k = Для того, чтобы определить шаг h, нужно воспользоваться формулой (2):
где R – размах, рассчитанный в нижеприведенной формуле (4).
Вычисление: h = 2,3/12=0,19 Таблица 3 − Интервальный ряд распределения длин 150 скрепок.
Одной из характеристик среднего значения является среднее арифметическое. При вычислении средней арифметической упорядоченного статистического ряда может быть использована формула (2):
где n – объем выборки, k – количество интервалов, xi – результат контроля i- ого изделия выборки (i = 1, 2,…n) ; hi – число повторений (частота). Таким же образом вычисляют среднюю арифметическую интервального ряда, согласно формуле (3), с той разницей, что в качестве значения признака следует принимать середину интервалов:
где К характеристикам рассеивания относятся: - дисперсия; - стандартное отклонение; - размах. Самой простой из них является размах, и, согласно формуле (4), является разностью наибольшего и наименьшего значения ряда наблюдений:
где R - размах;
Вычисление: R = 50,0-47,7=2,3 Наиболее часто для оценки рассеивания измеренных значений используют выборочную дисперсию - среднюю величину квадратов отклонений величины от средней арифметической. Т. к. выборка большого объема (n>30), то для расчета дисперсии нужно воспользоваться формулой (5), с помощью которой можно найти выборочную дисперсию для статистического упорядоченного ряда, и формулой (6) для расчета дисперсии интервального ряда:
Вместо дисперсии часто более удобно использовать стандартное отклонение (среднее квадратичное отклонение), вычисление которого приведено ниже в формуле (7):
Для упрощения вычислений и избегания ошибок при большом объеме вычислений при подсчете среднего арифметического, дисперсии и стандартного отклонения нужно оформлять результаты в табличном виде, т.е. в виде таблицы 4. Таблица 4 – Промежуточные вычисления для нахождения числовых характеристик интервального ряда из таблицы 3.
12 |



 ;
;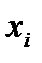
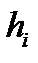

 , (1)
, (1)
 , (2)
, (2) , (2)
, (2) - средняя арифметическая;
- средняя арифметическая; ;
; ;
; , (3)
, (3) - середина интервала.
- середина интервала.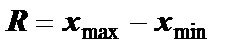 , (4)
, (4) - наибольшее значение;
- наибольшее значение;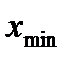 - наименьшее значение.
- наименьшее значение. , (5)
, (5) . (6)
. (6) = √
= √  . (7)
. (7)