 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Реактор непрерывного действия
Реакторы не прерывного действия с мешалками работают в стационарных условиях, так что параметры в любой точке системы не изменяются во времени. Реагенты непрерывно поступают в реактор, а продукты непрерывно отводят из него. В системах с хорошим перемешиванием поддерживается одинаковая концентрация во всем объеме аппарата. Такая система представляет собой предельный случай обратного перемешивания. Высокое значение движущей силы на входе в реактор мгновенно понижается на выходе из реактора. Для модели идеального смешения принимается ряд допущений. Допускается, что в результате интенсивного перемешивания устанавливаются абсолютно одинаковые условия в любой точке реактора: концентрации реагентов и продуктов, степени превращения реагентов, температура, скорость химической реакции и т. д В проточном реакторе идеального смешения концентрации элементов реакции в выходном потоке в рассматриваемый момент времени τi строго равны концентрациям тех же веществ в реакторе. Чтобы перечисленные допущения могли быть выполнены, необходимо принять еще одно допущение: переход от одной концентрации к другой в реакторе идеального смешения не должен иметь протяженности во времени. Изменение концентрации исходного реагента от начальной cJ,0 во входном потоке в данный момент времени τi до концентрации в реакторе сJ в этот же момент времени должно происходить мгновенно (скачкообразно). Приблизиться к режиму идеального смешения можно, обеспечив интенсивное перемешивание реакционной смеси механическими мешалками разного типа или циркуляционными насосами, создающими высокую кратность циркуляции. Смешение, близкое к идеальному смешению, легче выполнить в емкостных аппаратах с приблизительно равным диаметром и высотой. Так как в реакторе идеального смешения концентрации элементов реакции равномерно распределены по объему, то уравнение материального баланса (4.7), выведенное для элементарного объема, можно распространить на полный объем реактора. Рассмотрим два частных случая: периодический реактор идеального смешения и проточный реактор идеального смешения, работающий в стационарном режиме. Периодический реактор идеального смешения.В периодический реактор все реагенты вводят до начала реакции, а все продукты выводят из него только по окончании процесса. В ходе реакционного цикла никаких веществ в реактор не вводят и из него не выводят, так что общая масса реакционной смеси в реакторе остается постоянной, изменяется лишь ее состав. При составлении математического описания принимают, что реакционная смесь однородна по объему аппарата и ее состав зависит только от времени пребывания в периодическом реакторе.
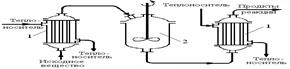
Рис. 5.1. Схемы реакторов идеального смешения Из общего уравнения материального баланса (4.7) в случае периодического реактора идеального смешения можно исключить два первых оператора, описывающих явления конвективного и диффузионного переноса вещества в аппарате. При отсутствии перемещения потока через реактор в произвольный момент времени между началом и окончанием процесса средняя линейная скорость элемента потока равна нулю, следовательно, и конвективный перенос в непроточном реакторе отсутствует. Заключение об отсутствии диффузионного переноса вытекает из допущений модели идеального смешения, так как диффузия возможна лишь при наличии градиента концентраций, а при равномерном распределении концентраций по объему он равен нулю. (Этот вывод справедлив не только для периодического, но и для проточного реактора идеального смешения.) Следовательно, уравнение материального баланса для периодического реактора идеального смешения примет вид
В уравнении (5.1) частная производная заменена на полную, так как в соответствии с допущениями идеального смешения концентрация с внутри реактора является функцией только одной переменной – времени. Уравнение материального баланса периодического реактора идеального смешения (5.1) совпадает с уравнением (3.2), дающим определение скорости химического превращения. Из одинакового вида уравнений косвенно можно сделать вывод, что гидродинамическая обстановка в периодическом реакторе идеального смешения не накладывает ограничений на химическую кинетику. Для проведения расчетов по уравнению (5.1) в его левую часть вместо wrJ(cJ)вводят конкретное кинетическое уравнение. Тогда можно рассчитать, например, время реакционного цикла, необходимое для достижения заданной глубины превращения (заданной конечной концентрации сJ,f):
Если вещество J – исходный реагент, то концентрацию cs можно выразить через его степень превращения:
Тогда
и уравнение (5.2) примет вид
Уравнения (5.2) и (5.3) позволяют также рассчитать зависимость концентрации реагента сJ или его степени превращения хJ от времени пребывания в реакторе (продолжительности реакционного цикла). В разные моменты времени условия в периодическом реакторе различные (концентрация реагентов, продуктов, скорость реакции и т. д.), однако в каждый данный момент времени из-за допущения об идеальности эти параметры строго одинаковы в объеме реактора (рис. 5.2). Время, рассчитанное по уравнению (5.2) или (5.3), является «чистым» временем, необходимым для проведения химического превращения. Однако для осуществления процесса в периодическом реакторе кроме этого «реакционного» времени нужно затратить вспомогательное время на загрузку реагентов, выведение реактора на нужный технологический режим, разгрузку и очистку. Полное время одного цикла работы периодического реактора суммируется из основного τхр и вспомогательного τвсп.
Рис. 5.2. Изменение концентрации исходного реагента Наличие τвсп как составной части времени цикла приводит к снижению производительности химического реактора (количество продукта, получаемого в единицу времени) и является одним из существенных недостатков периодических процессов вообще. Другие их недостатки – большие затраты ручного труда, сложность решения задач автоматизации (так как условия в реакторе во времени постоянно меняются). Однако периодические реакторы обычно можно приспособить к широкому диапазону условий реакций, что удобно при необходимости производить на одной установке различные химические продукты, например, в промышленности химических реактивов. Периодические реакторы с интенсивным перемешиванием, приближающимся к идеальному смешению, применяют в производствах реактивов, органических красителей, лекарственных препаратов – там, где для достижения достаточной глубины превращения требуется сравнительно длительное время, а объемы производства невелики. Периодические реакторы смешения часто применяют в микробиологической промышленности для культивирования аэробных микроорганизмов. Процесс культивирования для большинства микроорганизмов длится 48–72 ч, т. е. достаточно длителен. Интенсивное перемешивание в ферментаторе позволяет обеспечить равномерное распределение температуры, что особенно важно в таких процессах, так как даже небольшие локальные разогревы могут привести к гибели микроорганизмов. Изолированность реакционной системы в периодическом реакторе позволяет устранить опасность отравления микроорганизмов случайными примесями, которые могут попасть в аппарат при непрерывной подаче реагентов. Окончательное решение о целесообразности применения периодического или непрерывного процесса можно вынести лишь на основании экономической оценки (сравнения расходов на эксплуатацию, амортизацию, электроэнергию, пар, сырье и т. д.). Как правило, при проведении такого сравнения оказывается, что периодические процессы выгодны при относительно невысокой производственной мощности в тех случаях, когда получают дорогостоящие продукты. Проточный реактор идеального смешения в стационарном режиме.Если необходимо обеспечить получение большого количества продукта одинакового качества, химический процесс предпочитают проводить в непрерывно действующих реакторах с установившимся режимом. Распространенным видом таких проточных аппаратов являются реакторы смешения. Проточный реактор смешения может работать как в нестационарном режиме (пуск, выход на режим, остановка), так и в стационарном, установившемся режиме. Рассмотрим уравнение материального баланса для стационарного проточного реактора идеального смешения без циркуляции. Получим его, опять упрощая общее уравнение материального баланса (4.7). Для любого реактора идеального смешения, и в частности для проточного, из уравнения можно исключить оператор, описывающий диффузионный перенос. При стационарном режиме работы реактора из уравнения исключается производная дсJ/дτ,не равная нулю только при наличии накопления вещества в реакторе. Таким образом, в уравнении остаются только два члена, описывающие конвективный перенос вещества J и расход или образование этого вещества в ходе химической реакции. Оператор конвективного переноса (переноса импульса), записанный в уравнении (4.7) в дифференциальной форме, можно представить для проточного реактора идеального смешения в конечно-разностной форме. В соответствии с допущениями модели идеального смешения в проточном реакторе происходит дискретное конечное (а не бесконечно малое) изменение концентрации ∆сJ сразу же на входе в реактор. Заменим поэтому градиент концентрации на отношение конечного изменения концентрации ∆сJ к изменению координаты ∆z при прохождении реакционного потока через реактор со средней линейной скоростью
В выражении (5.4) ∆сJ равно разности концентраций на выходе из реактора cif и на входе в реактор сJ,0. Окончательно уравнение материального баланса проточного стационарного реактора идеального смешения можно представить так:
или
Это же уравнение можно получить и другим путем. Как указывалось, в качестве элементарного объема для реактора идеального смешения можно принять полный объем реактора V. При стационарном режиме работы реактора не происходит изменения постоянных по объему концентраций элементов реакции и во времени, следовательно, в качестве элементарного промежутка времени можно принять любой конечный временной интервал, например единицу времени (1 с, 1 мин или 1 ч). Количество вещества J, которое за единицу времени войдет в реактор с конвективным потоком, будет равно v0cJ,0,где v0 – объемный расход реакционного потока на входе в аппарат. За это же время выйдет из реактора с конвективным потоком количество вещества J = vfcJ,f,а расход вещества J (или его образование) в ходе химической реакции составит wrJ V. При этом скорость wrJ определяется концентрацией cJ,f. Стационарность процесса в проточном реакторе можно обеспечить, если объемные расходы на входе v0 и выходе vf равны между собой Тогда
Очевидно, что уравнение (5.6) тождественно уравнению (5.5). Величина Действительное время пребывания частиц в проточном реакторе смешения является случайной величиной в отличие от времени пребывания реагентов в периодическом реакторе. Пусть, например, в реактор введено N одинаковых частиц. В периодическом реакторе все они будут находиться равное время от загрузки до выгрузки. В проточном реакторе идеального смешения эти частицы мгновенно и равномерно распределяются по всему объему аппарата, и так как из аппарата непрерывно выходит поток продуктов, то в момент ввода частиц в реактор какое-то их количество может сразу же оказаться в выходном потоке. Некоторые частицы, равномерно распределяясь в новых порциях реакционной смеси, вошедшей в аппарат, могут находиться в нем бесконечно долго. Отсюда можно сделать вывод, что действительное время пребывания частиц в проточном реакторе – это случайная величина, которая может изменяться от 0 до ∞. Непрерывную случайную величину можно задать с помощью вероятностных характеристик, в частности функций распределения случайной величины. Использование в качестве характеристики времени пребывания частиц в проточном реакторе величины Для решения практических задач удобно концентрацию реагента cJ,fвыразить через его степень превращения хJ,f:
Уравнения материального баланса (5.5)–(5.7) для проточного реактора идеального смешения в стационарном режиме имеют ряд отличий от соответствующих уравнений для периодического реактора (5.2) и (5.3). Следует отметить, что балансовые уравнения стационарного реактора идеального смешения записываются сразу в виде конечного алгебраического уравнения в отличие от дифференциальной формы исходных уравнений для периодического реактора. В уравнение для периодического реактора скорость wr,Jследует подставлять в виде функциональной зависимости от концентрации wr,J(cj) или степени превращения wr,J(xj) и лишь после интегрирования уравнения возможна подстановка числовых значений. Этот факт, как и дифференциальная форма уравнений материального баланса, отражает зависимость параметров процесса в периодическом реакторе от времени. В стационарном режиме в любой точке реактора идеального смешения в любой момент времени концентрация постоянна. Следовательно, скорость реакции характеризуется каким-то одним конкретным числовым значением, определяемым этой концентрацией. Это число может быть сразу поставлено в уравнение материального баланса. Реакторы с движущимся слоем твердых частиц.Реакторы с движущимся слоем катализатора (рисунок 211). Движущийся слой гранулированного катализатора позволяет осуществить непрерывный процесс. Катализатор обычно имеет форму шариков. Для уменьшения истирания корпуса аппарата скорость движения катализатора невелика и составляет 12 - 48 см/мин. Катализатор движется под действием силы тяжести сверху вниз, т.е. возможен противоток или прямоток реагентов и катализато
Рисунок 211 - Реактор с движущимся слоем катализатора. Установки с движущимся катализатором, также как и установки с псевдоожиженным слоем, состоит из реагентов, регенератора и катализаторопроводов. Применяются схемы с однократным и двукратным подъемом катализатора. Подъем катализатора осуществляется либо пневмотранспортом, либо механически с помощью ковшового элеватора. Закономерности работы аппаратов с движущимся слоем катализатора сходны с закономерностями работы аппаратов с неподвижным катализатором. Можно лишь отметить, что порозность неподвижного слоя равна 0.4. В отечественной промышленности аппараты с движущимся слоем катализатора получили широкое распространение в основном в нефтеперерабатывающей промышленности. Проведение длительных процессов в присутствии катализаторов, быстро теряющих эффективность в режиме псевдоожиженного слоя, оказываются неэффективным. Одним из методов, позволяющих поддерживать активность таких катализаторов является применение реакторов с движущимся слоем. В этом случае гранулированный катализатор движется вдоль реактора, что дает возможность непрерывно вводить свежий катализатор, а следовательно, и обеспечивать постоянную каталитическую активность в течение длительного периода работы. Средняя каталитическая активность в этом случае зависит от соотношения скоростей подачи катализатора и сырья, иначе говоря, она распределяется весовым отношением расходов катализатора и сырья. Количественный характеристикой циркуляции катализатора является скорость циркуляции n - отношение катализатора, поступающего в реактор Gк (кг/ч), к расходу поступающего сырья Gc, (кг/ч)
Чем выше кратность циркуляции n, тем выше равновесная активность катализатора в реакторе и больше степень превращения сырья. Реакторы с неподвижным слоем твердых частиц.По способу теплообмена можно выделить три основных типа реакторов с неподвижным слоем, схемы которых представлены на рис. 1: - адиабатические реакторы (нет теплообмена); - реакторы с промежуточным отводом (подводом) тепла – многослойные (полочные) аппараты; - реакторы с непрерывным отводом (подводом) тепла – трубчатые аппараты. |




 (5.1)
(5.1) (5.2)
(5.2)

 (5.3)
(5.3)
 . Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V,член уравнения, описывающий конвективный перенос, примет вид
. Среднюю линейную скорость потока можно заменить через отношение объемного расхода v через реактор к площади поперечного сечения F. Тогда, с учетом того, что произведение F∆z равно объему реактора V,член уравнения, описывающий конвективный перенос, примет вид (5.4)
(5.4)
 . (5.5)
. (5.5)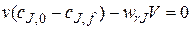 . (5.6)
. (5.6) = V/v в уравнении (5.5) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержимое проточного реактора. Эту величину называют средним временем пребывания реагентов в проточном реакторе.
= V/v в уравнении (5.5) измеряется в единицах времени и характеризует среднее время, в течение которого обновляется содержимое проточного реактора. Эту величину называют средним временем пребывания реагентов в проточном реакторе. . (5.7)
. (5.7) ров.
ров. , увеличение этого отношения говорит о более высокой средней активности катализатора. Схема установки с движущимся слоем катализатора предусматривает регенератор, расположенный рядом с реактором или совмещенный аппарат. Так что регенерированный катализатор сразу же возвращается в реактор. Циркуляция катализатора необходима для поддержания определенного уровня его активности в реакторе с движущимся слоем катализатора.
, увеличение этого отношения говорит о более высокой средней активности катализатора. Схема установки с движущимся слоем катализатора предусматривает регенератор, расположенный рядом с реактором или совмещенный аппарат. Так что регенерированный катализатор сразу же возвращается в реактор. Циркуляция катализатора необходима для поддержания определенного уровня его активности в реакторе с движущимся слоем катализатора.