 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Образец выполнения задачи 3.2 12
Груз массой m1 = 10 кг, двигаясь поступательно со скоростью v = 5 м/с по горизонтальной поверхности, сталкивается с нижним концом висящего вертикально однородного стержня массой m2 = 30 кг и длиной I = 0,5 м (рис. 1). Считая удар абсолютно неупругим, определить угловую скорость стержня w и скорость груза после удара v, а также величины действующих ударных импульсов. Найти также потерянную при ударе кинетическую энергию системы.
Рис. 3.1. Схема задачи
Решение. Если в качестве механической системы рассматривать груз и стержень, то возникающая между ними ударная сила окажется силой внутренней (ударный импульс Применим к системе теорему об изменении кинетического момента при ударе относительно оси вращения стержня z:
В данном случае
и кинетический момент системы в процессе удара сохранится: Kz = (Kz)0. До удара стержень был неподвижен и кинетический момент был лишь у груза (момент его количества движения После удара скорость груза изменится и станет равной некоторой величине u, а стержень приобретет некоторую угловую скорость ω и кинетический момент Jzω, где
— осевой момент инерции стержня. Таким образом, после удара
Кz = m1 u l + Jzω. Поскольку удар является абсолютно неупругим (т. е. отсутствует отскок), то и = ω l, тогда
Приравнивая кинетические моменты до удара и после него, получаем
Скорость груза после удара u = ω l = 2,5 м/с. Для вычисления ударного импульса S между грузом и стержнем
Рис.3.2. Импульсы взаимодействия груза
применим к грузу (рис. 2) теорему об изменении количества движения при ударе В проекции на горизонтальную ось имеем т1 и - т1 v = - S, откуда S = т1 (v - и) = 25 Н c. Чтобы вычислить ударные импульсы на оси стержня, применим к нему теорему об изменении количества движения при ударе, учитывая, что количество движения тела равно произведению его массы на скорость центра масс (рис. 3).
Рис. 3.3. Импульсы взаимодействия груза и стержня
До удара стержень был неподвижен и (Qо = 0, после удара Q = m2vc, где
В проекции на ось х теорема дает т2vc - 0 = S + S0х> откуда S0х = т2vc - S = 12,5 Н × c. Проекции на ось у количества движения стержня до и после удара нулевые, и тогда из теоремы легко видеть, что S0у = 0. Таким образом, ударный импульс на оси стержня So = S0х = 12,5 Н × c. Определим потерянную в процессе удара кинетическую энергию. До удара двигался только груз и его кинетическая энергия была
После удара двигались и груз, и стержень; общую кинетическую энергию системы находим
Таким образом, потерянная кинетическая энергия Т0 - Т = 62,5 Дж. Последний результат можно было получить иначе, используя теорему Карно: потеря кинетической энергии при абсолютно неупругом ударе равна кинетической энергии потерянных скоростей
Потерянная кинетическая энергия переходит в тепло и необратимые деформации. Ответ: w = 5 с-1; и = 2,5 м/с; S = 25 Н×c; S0 = 12,5 Н×c; Т0 - Т = 62,5 Дж.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Тарг, С. М. Краткий курс теоретической механики/ С. М. Тарг. – М.: Высшая школа, 2004. 2. Бать, И. М. Теоретическая механика в примерах и хадачах/ И. М. Бать [и др. ]. – М.: Наука, 1973. – Т. 1, 2, 3. 3. Дорожкина, В. В. Сборник заданий по теоретической механике. Статика/ В. В. Дорожкина [и др. ]. – СПб.: Лань, 2012. 4. Диевский, В. А. Теоретическая механика. Сборник заданий/ В. А. Диевский, И. А. Малышева. – СПб.: Лань, 2009.
12 |




 ), а внешним ударным будет лишь импульс на оси вращения стержня, который разложим на составляющие
), а внешним ударным будет лишь импульс на оси вращения стержня, который разложим на составляющие 

 ): (Кz)0 =m1v l.
): (Кz)0 =m1v l.

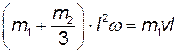 , откуда
, откуда  .
.
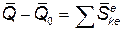 .
.


 .
. . Для груза потерянная скорость равна v - и, для стержня потерянная угловая скорость равна 0 - w = - w, и тогда
. Для груза потерянная скорость равна v - и, для стержня потерянная угловая скорость равна 0 - w = - w, и тогда .
.