 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Образец выполнения задачи 3.1 12
III. ДИНАМИКА
Задача 3.1. Динамика материальной точки Силы, заданные формулами, измеряют в Н.
1. По шероховатой наклонной плоскости, составляющей угол α = 30° с горизонтом, опускается без начальной скорости тело. Определить, в течение какого времени тело опустится на высоту h = 10 м по вертикали, если коэффициент трения скольжения f = 0,1.
2. На тело массой m, движущееся по горизонтальной гладкой поверхности вдоль оси х, действует сила, проекция которой равна Fх = 0,25 m x. В начальный момент тело находилось в покое в точке xo = 1 м. Определить скорость тела в момент, когда координата станет равной х = 5 м.
3. Сила тяги винтов вертолета массой m при его вертикальном подъеме из состояния покоя в 1,5 раза превышает его вес. Сопротивление воздуха пропорционально скорости
4. Лодке массой m = 100 кг сообщается начальная скорость vo = 4 м/с. При движении на лодку действует сила сопротивления, пропорциональная квадрату скорости R = 5 v2. Определить, в течение какого времени скорость лодки уменьшится в два раза.
5. Телу сообщается начальная скорость v0 = 6,6 м/с, и оно начинает скользить вверх по шероховатой наклонной плоскости, составляющей угол α = 30° с горизонтом. Коэффициент трения скольжения f = 0,2. Определить время достижения наивысшего положения тела и пройденный телом за это время путь.
6. На тело массой m, движущееся по горизонтальной гладкой поверхности вдоль оси х, действует сила, проекция которой равна Fх = − 0,36 m x. В начальный момент х0 = 0 и проекция скорости Vxo = 3 м/с. Определить максимальное значение координаты х тела.
7. Груз массой m = 10 кг опускается вертикально на парашюте без начальной скорости. Сопротивление воздуха пропорционально скорости
8. В момент выключения мотора катер массой m = 200 кг имел скорость. Определить путь, который пройдет катер до того момента времени, когда скорость катера уменьшится в десять раз. Сила сопротивления движению пропорциональна квадрату скорости R = 8 v2.
9. Тело начинает скользить вниз по шероховатой наклонной плоскости, составляющей угол α = 30° с горизонтом, с начальной скоростью vo = 2 м/с. Коэффициент трения скольжения f = 0,4. Определить путь, пройденный телом за время t = 2с.
0. Материальная точка массой m = 2 кг движется из состояния покоя по горизонтальной гладкой поверхности вдоль оси х под действием силы, проекция которой равна Fх = 3 (1 − 0,5 t ). Определить скорость и координату точки в тот момент времени, когда сила станет равной нулю. Начальную координату точки считать нулевой.
Образец выполнения задачи 3.1
Тело массой m = 15 кг поднимается по гладкой наклонной плоскости, составляющей угол α = 30°с горизонтом, получив начальную скорость v0 = 10 м/с. Сопротивление среды пропорционально скорости Решение. Изобразим тело на наклонной плоскости (рис. 3.1)
Рис. 3.1. Рисунок к задаче 3.1 Составим уравнения движения тела в проекции на ось Ох
Уравнение (3.1) можно записать в виде
Уравнение (3.2) является линейным дифференциальным уравнением первого порядка с разделяющимися переменными. Представим производную от скорости как отношение дифференциалов функции и независимой переменной
и проведём разделение переменных
Проинтегрируем соотношение (3.3)
Используя свойства дифференциала и определённого интеграла, выполним замену аргумента интегрирования в левой части
Интегралы в левой и правой части соотношения (3.5) являются табличными и по формуле Ньютона – Лейбница получим
или
Пусть t = T время, при котором v = 0. Из соотношения (3.6) получим
откуда находим время, за которое тело остановится
Ответ: 0,86 с.
12 |



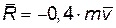 . Определить скорость подъема в момент t = 5 с, а также максимальную скорость вертолета.
. Определить скорость подъема в момент t = 5 с, а также максимальную скорость вертолета. . Определить скорость груза в момент времени t = 1 с.
. Определить скорость груза в момент времени t = 1 с. . Определить время, прошедшее до остановки тела.
. Определить время, прошедшее до остановки тела.
 (3.1)
(3.1) (3.2)
(3.2)
 . (3.3)
. (3.3) . (3.4)
. (3.4) (3.5)
(3.5)
 . (3.6)
. (3.6) ,
, .
.