 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Определение касательных напряжений
При поперечном изгибе и кручении рассматриваемых оболочек в обшивке возникают касательные напряжения, которые связаны с касательными усилиями равенством  , где , где 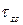 - среднее по толщине касательное напряжение вдоль контура сечения. Для определения касательного напряжения рассмотрим равновесие бесконечно малого элемента обшивки, нагруженного нормальными и касательными усилиями. Проектируя усилия на направление оси - среднее по толщине касательное напряжение вдоль контура сечения. Для определения касательного напряжения рассмотрим равновесие бесконечно малого элемента обшивки, нагруженного нормальными и касательными усилиями. Проектируя усилия на направление оси  , получим известное выражение уравнения равновесия , получим известное выражение уравнения равновесия  , () , ()
откуда интегрированием по  определим касательное усилие определим касательное усилие  . (6.11) . (6.11)
Здесь  - поток в месте разреза сечения, где - поток в месте разреза сечения, где 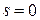 . . Определение касательных усилий. Подставим нормальное усилие  из уравнения (6.9) в уравнение (6.11) и получим выражение из уравнения (6.9) в уравнение (6.11) и получим выражение  , (6.12) , (6.12)
где штрихи означают производные по координате  . Вводя обозначение . Вводя обозначение  - отсеченная жесткость сечения с учетом жесткости стрингеров; - отсеченная жесткость сечения с учетом жесткости стрингеров;
 - отсеченный статический момент с учетом модуля упругости относительно оси - отсеченный статический момент с учетом модуля упругости относительно оси  и учетом стрингеров; и учетом стрингеров;
 - отсеченный статический момент с учетом модуля упругости относительно оси - отсеченный статический момент с учетом модуля упругости относительно оси  и учетом стрингеров. и учетом стрингеров.
Учитывая, что производные от момента есть перерезывающие силы в сечении, т.е.  и и  , можно увидеть, что выражение в круглых скобках соответствует потокам касательных сил , можно увидеть, что выражение в круглых скобках соответствует потокам касательных сил  от поперечной нагрузки для открытого сечения, тогда от поперечной нагрузки для открытого сечения, тогда  есть касательный поток, компенсирующий разрез в рассматриваемом сечении. В главных центральных осях поток от перерезывающих сил есть касательный поток, компенсирующий разрез в рассматриваемом сечении. В главных центральных осях поток от перерезывающих сил  в месте разреза равен нулю, так как эквивалентные статические потоки для сечения равны нулю. Следовательно, в уравнении (6.12) при удовлетворении этого условия должно выполняться условие в месте разреза равен нулю, так как эквивалентные статические потоки для сечения равны нулю. Следовательно, в уравнении (6.12) при удовлетворении этого условия должно выполняться условие  . Тогда уравнение (6.12) примет вид . Тогда уравнение (6.12) примет вид  . (6.13) . (6.13)
Таким образом, при вычислении потока  удобно считать, что контур разрезан в какой-то точке удобно считать, что контур разрезан в какой-то точке  , тогда постоянный поток , тогда постоянный поток  можно считать компенсирующим этот условный разрез. Уравнение (6.13) можно переписать в виде можно считать компенсирующим этот условный разрез. Уравнение (6.13) можно переписать в виде  , где , где  или или  . (6.14) . (6.14)
Таким образом, поток  производится поперечными силами Qx и Qy. Эти же слагаемые потока от поперечных сил в уравнении (6.14) удовлетворяют уравнениям равновесия всех сил на оси производится поперечными силами Qx и Qy. Эти же слагаемые потока от поперечных сил в уравнении (6.14) удовлетворяют уравнениям равновесия всех сил на оси 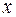 и и  . Удовлетворим последнее статическое уравнение равновесия крутящих моментов относительно продольной оси . Удовлетворим последнее статическое уравнение равновесия крутящих моментов относительно продольной оси  . Суммарный поток . Суммарный поток  должен сводится к крутящему моменту должен сводится к крутящему моменту  или или  . (6.15) . (6.15)
Первый контурный интеграл определяет удвоенную площадь внутри контура, где радиус отсчитывается относительно произвольной точки. Как видно из рис. 6.9, элементарная площадь  равна удвоенной площади элементарного треугольника с основанием равна удвоенной площади элементарного треугольника с основанием  . . 
Рис. 6.9. К определению удвоенной площади внутри контура Интегрируя вдоль контура, найдем удвоенную площадь, ограниченную контуром, т.е.  . Тогда из (6.15) находим поток . Тогда из (6.15) находим поток  
или, подставляя в выражение значение  , перепишем его в виде , перепишем его в виде  . .
Тогда касательный поток можно представить в виде  , (6.16) , (6.16)
где  и и  . (6.17) . (6.17) Если  , то получим формулу Бредта для определения потока от кручения , то получим формулу Бредта для определения потока от кручения  . .
Для прямоугольного контура с размерами сторон  и и   . . Определение перемещений Осевое смещение  и углы поворотов поперечного сечения и углы поворотов поперечного сечения  и и  относительно осей относительно осей 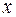 и и  были уже определены уравнениями (6.10). Теперь мы определяем угол вращения поперечного сечения относительно оси были уже определены уравнениями (6.10). Теперь мы определяем угол вращения поперечного сечения относительно оси  . В соответствии с теоремой Кастильяно, погонный угол вращения определяется производной от потенциальной энергии по моменту вращения, действующего в сечении, т.е. . В соответствии с теоремой Кастильяно, погонный угол вращения определяется производной от потенциальной энергии по моменту вращения, действующего в сечении, т.е.
 , ,
где потенциальная энергия для ортотропной оболочки равна  . . Усилие  известно и для изотропной и ортотропной структуры с потоком известно и для изотропной и ортотропной структуры с потоком  не связано (коэффициенты не связано (коэффициенты  ) и при варьировании по ) и при варьировании по  на угол поворота не влияет. Если учитывать, что на угол поворота не влияет. Если учитывать, что  есть функция от есть функция от  , то погонный угол можно выразить как , то погонный угол можно выразить как  и изменение угла по длине определяется интегрированием выражения и изменение угла по длине определяется интегрированием выражения  , где , где 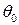 определяется из условия закрепления оболочки. Тогда для вычисления погонного угла поворота для фиксированного сечения с координатой по длине оболочки определяется из условия закрепления оболочки. Тогда для вычисления погонного угла поворота для фиксированного сечения с координатой по длине оболочки 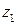 и с известными силовыми функциями в этом сечении получим формулу в виде и с известными силовыми функциями в этом сечении получим формулу в виде  . (6.18) . (6.18)
Если сечение имеет ось симметрии 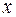 , то , то  , а если две оси симметрии, то и , а если две оси симметрии, то и  , тогда , тогда  . . Используя теорему Кастильяно можно вычислять углы поворотов сечения относительно осей 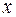 и и  . Например, поворот сечения относительно оси . Например, поворот сечения относительно оси 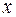 запишется запишется 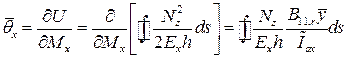 . .
|




 , где
, где 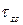 - среднее по толщине касательное напряжение вдоль контура сечения. Для определения касательного напряжения рассмотрим равновесие бесконечно малого элемента обшивки, нагруженного нормальными и касательными усилиями. Проектируя усилия на направление оси
- среднее по толщине касательное напряжение вдоль контура сечения. Для определения касательного напряжения рассмотрим равновесие бесконечно малого элемента обшивки, нагруженного нормальными и касательными усилиями. Проектируя усилия на направление оси  , получим известное выражение уравнения равновесия
, получим известное выражение уравнения равновесия , ()
, () определим касательное усилие
определим касательное усилие . (6.11)
. (6.11) - поток в месте разреза сечения, где
- поток в месте разреза сечения, где 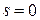 .
. из уравнения (6.9) в уравнение (6.11) и получим выражение
из уравнения (6.9) в уравнение (6.11) и получим выражение , (6.12)
, (6.12) - отсеченная жесткость сечения с учетом жесткости стрингеров;
- отсеченная жесткость сечения с учетом жесткости стрингеров; - отсеченный статический момент с учетом модуля упругости относительно оси
- отсеченный статический момент с учетом модуля упругости относительно оси  и учетом стрингеров;
и учетом стрингеров; - отсеченный статический момент с учетом модуля упругости относительно оси
- отсеченный статический момент с учетом модуля упругости относительно оси  и учетом стрингеров.
и учетом стрингеров. и
и  , можно увидеть, что выражение в круглых скобках соответствует потокам касательных сил
, можно увидеть, что выражение в круглых скобках соответствует потокам касательных сил  от поперечной нагрузки для открытого сечения, тогда
от поперечной нагрузки для открытого сечения, тогда  . Тогда уравнение (6.12) примет вид
. Тогда уравнение (6.12) примет вид . (6.13)
. (6.13) , тогда постоянный поток
, тогда постоянный поток  , где
, где или
или  . (6.14)
. (6.14)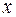 и
и  . Удовлетворим последнее статическое уравнение равновесия крутящих моментов относительно продольной оси
. Удовлетворим последнее статическое уравнение равновесия крутящих моментов относительно продольной оси  должен сводится к крутящему моменту
должен сводится к крутящему моменту или
или  . (6.15)
. (6.15) равна удвоенной площади элементарного треугольника с основанием
равна удвоенной площади элементарного треугольника с основанием  .
.
 . Тогда из (6.15) находим поток
. Тогда из (6.15) находим поток 
 .
. , (6.16)
, (6.16) и
и  . (6.17)
. (6.17) , то получим формулу Бредта для определения потока от кручения
, то получим формулу Бредта для определения потока от кручения .
. и
и 
 .
. и углы поворотов поперечного сечения
и углы поворотов поперечного сечения  и
и  относительно осей
относительно осей  ,
, .
. известно и для изотропной и ортотропной структуры с потоком
известно и для изотропной и ортотропной структуры с потоком  ) и при варьировании по
) и при варьировании по  на угол поворота не влияет. Если учитывать, что
на угол поворота не влияет. Если учитывать, что  и изменение угла по длине определяется интегрированием выражения
и изменение угла по длине определяется интегрированием выражения  , где
, где 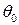 определяется из условия закрепления оболочки. Тогда для вычисления погонного угла поворота для фиксированного сечения с координатой по длине оболочки
определяется из условия закрепления оболочки. Тогда для вычисления погонного угла поворота для фиксированного сечения с координатой по длине оболочки 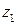 и с известными силовыми функциями в этом сечении получим формулу в виде
и с известными силовыми функциями в этом сечении получим формулу в виде . (6.18)
. (6.18) , а если две оси симметрии, то и
, а если две оси симметрии, то и  , тогда
, тогда  .
.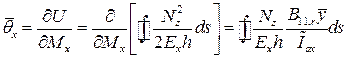 .
.