 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Определение нормальных напряжений
При изложении материала использованы результаты работ монографий В.В. Васильева [3], А.А.Дудченко [2]. Рассмотрим применение балочной теории для расчета длинномерных конструкций типа кессонов крыла, поверхностей хвостового оперения и удлиненных фюзеляжей с произвольной формой поперечного сечения. Считаем, что рассматриваемые расчетные конструкции являются длинномерными. Длина оболочки намного больше, чем размеры ее поперечного сечения и последнее, в свою очередь, намного больше, чем толщина обшивки, причем отсутствуют вырезы и резкое изменение жесткости обшивки и подкрепляющих элементов по координате 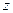 . Такие оболочки, как структурный элемент, работают на растяжение-сжатие, поперечный изгиб, кручение. Считаем, что на оболочку типа кессона крыла действуют осевые силы Pz, изгибающие моменты . Такие оболочки, как структурный элемент, работают на растяжение-сжатие, поперечный изгиб, кручение. Считаем, что на оболочку типа кессона крыла действуют осевые силы Pz, изгибающие моменты  и и 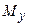 , крутящий момент Mz, и поперечные силы Qx и Qy (рис. 6.6), которые, в общем случае вызваны мембранными напряжениями , крутящий момент Mz, и поперечные силы Qx и Qy (рис. 6.6), которые, в общем случае вызваны мембранными напряжениями  и и  . Распределение нормальных напряжений . Распределение нормальных напряжений  в поперечном сечении должно быть статически эквивалентным действующим в этом сечении моментам в поперечном сечении должно быть статически эквивалентным действующим в этом сечении моментам  , , 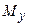 и осевой силе Pz. и осевой силе Pz. 
Рис. 6.6. Структурный элемент оболочки кессонного типа с нагрузками Сформулируем гипотезы и допущения, на которых построена расчетная теория - балочная теория: 1. Примем, что продольные деформации  в любом поперечном сечении оболочки распределяются по закону плоскости в любом поперечном сечении оболочки распределяются по закону плоскости  . . 2. Оболочка считается безмоментной, так как толщина стенки оболочки мала. Поэтому нормальные усилия и касательные потоки определяются как произведение соответствующего напряжения на толщину оболочки. Подкрепляющие продольные элементы воспринимают только продольные напряжения  . . 3. Все нагрузки, действующие на рассматриваемую конструкцию, в каждом сечении  сводятся к изгибающим моментам сводятся к изгибающим моментам 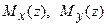 , крутящему моменту , крутящему моменту  , осевой силе , осевой силе  и поперечным силам и поперечным силам  (см. рис.6.6). (см. рис.6.6). 4. Композиционный материал в конструкции остается упругим вплоть до разрушения и связь между напряжениями и деформациями определяются законом Гука, при этом считается, что обшивка и стенки не теряют устойчивости. 5. В композиционных авиационных конструкциях при действии перечисленных нагрузок можно считать, что контурные усилия 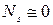 ( (  , ,  - толщина обшивки), в то время как - толщина обшивки), в то время как 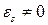 . Эти усилия существенно меньше двух других усилий, действующих в оболочке. . Эти усилия существенно меньше двух других усилий, действующих в оболочке. 6. Расчетная часть цилиндрической оболочки считается длиной, регулярной по длине, без вырезов, без резкого изменения жесткости и нагрузок, без учета условий закрепления. Принимаем, что продольные деформации связаны с продольными перемещениями соотношением 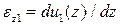 , которые являются постоянными в поперечном сечении , которые являются постоянными в поперечном сечении  . Введем в сечении две другие деформации . Введем в сечении две другие деформации 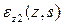 и и 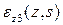 , вызванные изгибающими моментами , вызванные изгибающими моментами 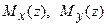 относительно осей относительно осей  и и  соответственно (рис. 6.6), которые приводят к двум продольным перемещениям соответственно (рис. 6.6), которые приводят к двум продольным перемещениям  и и  , переменным по координате , переменным по координате  . От действия изгибающих моментов плоскость сечения должна поворачиваться вокруг соответствующих осей, а величина перемещений . От действия изгибающих моментов плоскость сечения должна поворачиваться вокруг соответствующих осей, а величина перемещений  и и  должна быть пропорциональна координатам сечения должна быть пропорциональна координатам сечения  или или  . Тогда смещение . Тогда смещение  при повороте сечения относительно оси при повороте сечения относительно оси  будет пропорционально координате будет пропорционально координате  (рис. 6.7), т.е. (рис. 6.7), т.е.  , где , где  (z) является угловым вращением вокруг оси x. В этом случае деформация поперечного сечения (z) является угловым вращением вокруг оси x. В этом случае деформация поперечного сечения 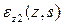 будет будет  . Здесь и далее штрих означает производную от функции по координате z. . Здесь и далее штрих означает производную от функции по координате z. 
Рис. 6.7. Смещение  при повороте сечения относительно оси при повороте сечения относительно оси  Аналогично мы определим смещение  при повороте сечения относительно оси при повороте сечения относительно оси  , которое запишем как , которое запишем как  , где , где  - угловое вращение сечения вокруг оси y. В этом случае деформация поперечного сечения - угловое вращение сечения вокруг оси y. В этом случае деформация поперечного сечения 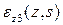 будет равна будет равна  . Таким образом, полная осевая деформация поперечного сечения будет иметь вид . Таким образом, полная осевая деформация поперечного сечения будет иметь вид  . (6.2) . (6.2)
Так как продольная деформация  связана с продольным перемещением сечения связана с продольным перемещением сечения 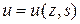 соотношением соотношением  , то интегрирование этого выражения с учетом (6.2) определяет перемещение в виде , то интегрирование этого выражения с учетом (6.2) определяет перемещение в виде  . (6.3) . (6.3)
В уравнении (6.3) слагаемые соответствуют:  - осевое смещение поперечного сечения, а - осевое смещение поперечного сечения, а  и и  - углы поворота относительно осей - углы поворота относительно осей  и и  . Положительные углы соответствуют направлениям моментов . Положительные углы соответствуют направлениям моментов  и и 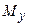 , показанные на рис. 6.6. Произвольная функция интегрирования , показанные на рис. 6.6. Произвольная функция интегрирования  определяет отклонение поперечного сечения от его плоского деформирования поперечного сечения и учитывает свободную депланацию (искажение) сечения, но не влияет на нормальные напряжения. Свободное деформирование не оказывает влияния на состояние продольного напряжения, которое в соответствии закона Гука имеет вид определяет отклонение поперечного сечения от его плоского деформирования поперечного сечения и учитывает свободную депланацию (искажение) сечения, но не влияет на нормальные напряжения. Свободное деформирование не оказывает влияния на состояние продольного напряжения, которое в соответствии закона Гука имеет вид  , где , где  имеет вид (6.2). Это выражение точно соответствует принятой гипотезе деформирования сечения. Такой закон получается из-за принятого допущения, что имеет вид (6.2). Это выражение точно соответствует принятой гипотезе деформирования сечения. Такой закон получается из-за принятого допущения, что 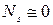 ( (  ). Для конструкции из композиционного материала физический закон получим после рассмотрения следующих преобразований. Запишем соотношения закона Гука для плоской задачи ортотропного материала с учетом гипотезы ). Для конструкции из композиционного материала физический закон получим после рассмотрения следующих преобразований. Запишем соотношения закона Гука для плоской задачи ортотропного материала с учетом гипотезы 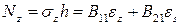 ; ;
 . .
Исключая  из этих выражений, получим связь между усилием из этих выражений, получим связь между усилием  и деформацией и деформацией  в виде в виде  [1], что соответствует предыдущей записи с учетом толщины материала ( [1], что соответствует предыдущей записи с учетом толщины материала (  - толщина обшивки). - толщина обшивки). Считая, что влияние искажения поперечного сечения и, соответственно, перераспределение нормальных напряжений, будет только в районе закрепления конструкции, физический закон определяется выражением  . (6.4) . (6.4)
Для определения нормальных усилий  необходимо в выражении (6.4) найти значения коэффициентов необходимо в выражении (6.4) найти значения коэффициентов  . Распределение нормальных усилий в сечении должно быть эквивалентно действующим моментам . Распределение нормальных усилий в сечении должно быть эквивалентно действующим моментам  , ,  и осевой силе и осевой силе  . Тогда статические соотношения можно записать . Тогда статические соотношения можно записать  (6.5) (6.5)
и дополнительные статические уравнения, обеспечивающие равновесие сил в направлениях осей  и и  , а также уравнение крутящих моментов относительно оси , а также уравнение крутящих моментов относительно оси  , которые будут рассмотрены позднее и имеют вид: , которые будут рассмотрены позднее и имеют вид: 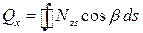 , , 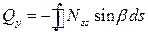 , ,  , (6.6) , (6.6)
где r определяется равенством 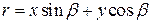 и является кротчайшим расстоянием между центром O и касательной к контуру сечения в точке М (рис. 6.8, это - перпендикуляр к касательной к контуру в т. М); Nzs – касательное усилие в обшивке; Qx и Qy – поперечные силы сечения; Mz – крутящий момент. и является кротчайшим расстоянием между центром O и касательной к контуру сечения в точке М (рис. 6.8, это - перпендикуляр к касательной к контуру в т. М); Nzs – касательное усилие в обшивке; Qx и Qy – поперечные силы сечения; Mz – крутящий момент. 
Рис. 6.8. К определению крутящего момента Раскрывая соотношения (6.5), получим  , ,
 , (6 .7) , (6 .7)
 . .
Здесь  - площадь сечения - площадь сечения  -го продольного элемента; -го продольного элемента;  - модуль упругости в продольном направлении обшивки, который может быть переменным по контуру. - модуль упругости в продольном направлении обшивки, который может быть переменным по контуру. Вводя обозначения 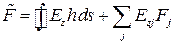 - жесткость сечения на растяжение; - жесткость сечения на растяжение;  - эквивалент статического момента относительно оси - эквивалент статического момента относительно оси  ; ;  - эквивалент статического момента относительно оси - эквивалент статического момента относительно оси  ; ;
 - изгибная жесткость поперечного сечения относительно оси - изгибная жесткость поперечного сечения относительно оси  ; ;
 - изгибная жесткость поперечного сечения относительно оси - изгибная жесткость поперечного сечения относительно оси  ; ;
 - эквивалент центробежному моменту инерции сечения. - эквивалент центробежному моменту инерции сечения.
Тогда уравнения (6.7) примут вид  ; ;
 ; (6.8) ; (6.8)
 . .
Разрешая уравнения относительно неизвестных параметров и определяя их, запишем нормальное усилие для  - ой точки сечения композитной оболочки - ой точки сечения композитной оболочки  . (6.9) . (6.9)
Здесь  - коэффициент несимметрии сечения оболочки; - коэффициент несимметрии сечения оболочки;  , ,  - обобщенные координаты точек сечения в главных центральных осях; - обобщенные координаты точек сечения в главных центральных осях;  - координаты центра тяжести сечения; - координаты центра тяжести сечения;
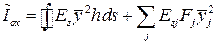 , , 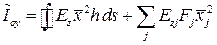 , ,  - эквивалент моментов инерции сечения относительно главных центральных осей. - эквивалент моментов инерции сечения относительно главных центральных осей.
В записанной формуле проводится автоматическое редуцирование жесткостных характеристик материала панелей сечения, где индекс  учитывает реальные свойства учитывает реальные свойства  - го стрингера в этой точке. Кроме того, при определении усилия - го стрингера в этой точке. Кроме того, при определении усилия  , в самой величине которого заключена толщина обшивки, может использоваться для нахождения этой толщины в задачах проектирования. , в самой величине которого заключена толщина обшивки, может использоваться для нахождения этой толщины в задачах проектирования. Решение системы (6.8) позволяет определять неизвестные, входящие в эти уравнения. Искомые параметры имеют вид:  ; ;  ; ;  . .
Если сечение конструкции имеет ось симметрии, то центробежный момент инерции  , коэффициент , коэффициент 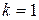 и во всех полученных выражениях соответствующие слагаемые пропадут. и во всех полученных выражениях соответствующие слагаемые пропадут. Таким образом, задача определения нормальных напряжений и усилий, благодаря введенным гипотезам, является статически определимой задачей.
|




 . Такие оболочки, как структурный элемент, работают на растяжение-сжатие, поперечный изгиб, кручение. Считаем, что на оболочку типа кессона крыла действуют осевые силы Pz, изгибающие моменты
. Такие оболочки, как структурный элемент, работают на растяжение-сжатие, поперечный изгиб, кручение. Считаем, что на оболочку типа кессона крыла действуют осевые силы Pz, изгибающие моменты  и
и 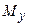 , крутящий момент Mz, и поперечные силы Qx и Qy (рис. 6.6), которые, в общем случае вызваны мембранными напряжениями
, крутящий момент Mz, и поперечные силы Qx и Qy (рис. 6.6), которые, в общем случае вызваны мембранными напряжениями  и
и  . Распределение нормальных напряжений
. Распределение нормальных напряжений  в поперечном сечении должно быть статически эквивалентным действующим в этом сечении моментам
в поперечном сечении должно быть статически эквивалентным действующим в этом сечении моментам 
 в любом поперечном сечении оболочки распределяются по закону плоскости
в любом поперечном сечении оболочки распределяются по закону плоскости  .
. сводятся к изгибающим моментам
сводятся к изгибающим моментам 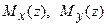 , крутящему моменту
, крутящему моменту  , осевой силе
, осевой силе  и поперечным силам
и поперечным силам  (см. рис.6.6).
(см. рис.6.6).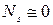 (
(  ,
,  - толщина обшивки), в то время как
- толщина обшивки), в то время как 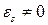 . Эти усилия существенно меньше двух других усилий, действующих в оболочке.
. Эти усилия существенно меньше двух других усилий, действующих в оболочке.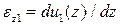 , которые являются постоянными в поперечном сечении
, которые являются постоянными в поперечном сечении 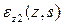 и
и 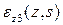 , вызванные изгибающими моментами
, вызванные изгибающими моментами  и
и  соответственно (рис. 6.6), которые приводят к двум продольным перемещениям
соответственно (рис. 6.6), которые приводят к двум продольным перемещениям  и
и  , переменным по координате
, переменным по координате  . От действия изгибающих моментов плоскость сечения должна поворачиваться вокруг соответствующих осей, а величина перемещений
. От действия изгибающих моментов плоскость сечения должна поворачиваться вокруг соответствующих осей, а величина перемещений  или
или  . Тогда смещение
. Тогда смещение  , где
, где  (z) является угловым вращением вокруг оси x. В этом случае деформация поперечного сечения
(z) является угловым вращением вокруг оси x. В этом случае деформация поперечного сечения  . Здесь и далее штрих означает производную от функции по координате z.
. Здесь и далее штрих означает производную от функции по координате z.
 , где
, где  - угловое вращение сечения вокруг оси y. В этом случае деформация поперечного сечения
- угловое вращение сечения вокруг оси y. В этом случае деформация поперечного сечения  . Таким образом, полная осевая деформация поперечного сечения будет иметь вид
. Таким образом, полная осевая деформация поперечного сечения будет иметь вид . (6.2)
. (6.2) связана с продольным перемещением сечения
связана с продольным перемещением сечения 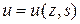 соотношением
соотношением  , то интегрирование этого выражения с учетом (6.2) определяет перемещение в виде
, то интегрирование этого выражения с учетом (6.2) определяет перемещение в виде . (6.3)
. (6.3) - осевое смещение поперечного сечения, а
- осевое смещение поперечного сечения, а  определяет отклонение поперечного сечения от его плоского деформирования поперечного сечения и учитывает свободную депланацию (искажение) сечения, но не влияет на нормальные напряжения. Свободное деформирование не оказывает влияния на состояние продольного напряжения, которое в соответствии закона Гука имеет вид
определяет отклонение поперечного сечения от его плоского деформирования поперечного сечения и учитывает свободную депланацию (искажение) сечения, но не влияет на нормальные напряжения. Свободное деформирование не оказывает влияния на состояние продольного напряжения, которое в соответствии закона Гука имеет вид  , где
, где  ). Для конструкции из композиционного материала физический закон получим после рассмотрения следующих преобразований. Запишем соотношения закона Гука для плоской задачи ортотропного материала с учетом гипотезы
). Для конструкции из композиционного материала физический закон получим после рассмотрения следующих преобразований. Запишем соотношения закона Гука для плоской задачи ортотропного материала с учетом гипотезы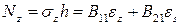 ;
; .
. из этих выражений, получим связь между усилием
из этих выражений, получим связь между усилием  и деформацией
и деформацией  [1], что соответствует предыдущей записи с учетом толщины материала (
[1], что соответствует предыдущей записи с учетом толщины материала (  - толщина обшивки).
- толщина обшивки). . (6.4)
. (6.4) необходимо в выражении (6.4) найти значения коэффициентов
необходимо в выражении (6.4) найти значения коэффициентов  . Распределение нормальных усилий в сечении должно быть эквивалентно действующим моментам
. Распределение нормальных усилий в сечении должно быть эквивалентно действующим моментам  ,
,  и осевой силе
и осевой силе  . Тогда статические соотношения можно записать
. Тогда статические соотношения можно записать (6.5)
(6.5) , которые будут рассмотрены позднее и имеют вид:
, которые будут рассмотрены позднее и имеют вид: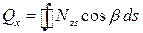 ,
, 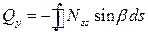 ,
,  , (6.6)
, (6.6)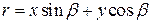 и является кротчайшим расстоянием между центром O и касательной к контуру сечения в точке М (рис. 6.8, это - перпендикуляр к касательной к контуру в т. М); Nzs – касательное усилие в обшивке; Qx и Qy – поперечные силы сечения; Mz – крутящий момент.
и является кротчайшим расстоянием между центром O и касательной к контуру сечения в точке М (рис. 6.8, это - перпендикуляр к касательной к контуру в т. М); Nzs – касательное усилие в обшивке; Qx и Qy – поперечные силы сечения; Mz – крутящий момент.
 ,
, , (6 .7)
, (6 .7) .
. - площадь сечения
- площадь сечения  -го продольного элемента;
-го продольного элемента;  - модуль упругости в продольном направлении обшивки, который может быть переменным по контуру.
- модуль упругости в продольном направлении обшивки, который может быть переменным по контуру.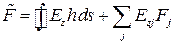 - жесткость сечения на растяжение;
- жесткость сечения на растяжение;  - эквивалент статического момента относительно оси
- эквивалент статического момента относительно оси  - эквивалент статического момента относительно оси
- эквивалент статического момента относительно оси  - изгибная жесткость поперечного сечения относительно оси
- изгибная жесткость поперечного сечения относительно оси  - изгибная жесткость поперечного сечения относительно оси
- изгибная жесткость поперечного сечения относительно оси  - эквивалент центробежному моменту инерции сечения.
- эквивалент центробежному моменту инерции сечения. ;
; ; (6.8)
; (6.8) .
. - ой точки сечения композитной оболочки
- ой точки сечения композитной оболочки . (6.9)
. (6.9) - коэффициент несимметрии сечения оболочки;
- коэффициент несимметрии сечения оболочки; ,
,  - обобщенные координаты точек сечения в главных центральных осях;
- обобщенные координаты точек сечения в главных центральных осях;  - координаты центра тяжести сечения;
- координаты центра тяжести сечения;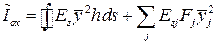 ,
, 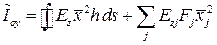 ,
,  - эквивалент моментов инерции сечения относительно главных центральных осей.
- эквивалент моментов инерции сечения относительно главных центральных осей. учитывает реальные свойства
учитывает реальные свойства  ;
;  ;
;  .
. , коэффициент
, коэффициент 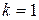 и во всех полученных выражениях соответствующие слагаемые пропадут.
и во всех полученных выражениях соответствующие слагаемые пропадут.