 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| С выходом на мировой рынок 12
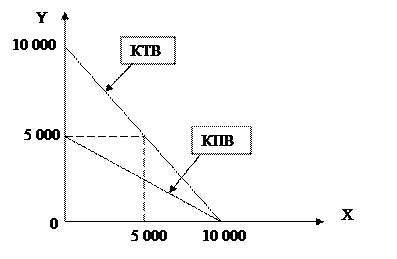
С выходом на мировой рынокотносительная цена блага стала равна 1. То есть предполагаемый бюджет студентов составит 10 000 (продавая 10 000 лекций по цене 1).И кривая производственных возможностей будет отличатся от кривой торговых возможностей . И снова используя функцию Кобба Дугласа, делим наш доход в соотношении
И получаем что 10 000: 2= 5 000, то есть они напишут 5 000 статей о снижении темпов экономического роста в развитых странах (У= 5 000) и прочтут 5 000 лекций друг другу по экономической теории (Х= 5 000).
Ответ: У=2500, Х=5000; У= 5 000, Х= 5 000
152. Василий Разгуляев решил жениться. За оставшиеся до свадьбы 4 часа он пожелал получить максимум удовольствия от своих любимых развлечений: проехать на мотоцикле, выпить пива и потанцевать с девушками. Известны функции полезности В.Разгуляева для этих видов досуга. Езда но мотоцикле: Uм(t) = 2ln(t-0,5); выпивка: Uв(t) = ln(t); танцы: Uт(t) = ln(t²) , где t – время, измеряемое в часах. Определите, сколько времени В.Разгуляев потратит на каждое из развлечений. Определите, каким образом изменится решение В.Разгуляева, если его мотоцикл сломается, а товарищ согласен одолжить ему свой не более, чем на 30 минут.
Uв(t) = ln(t) t>0 Uт(t) = ln(t²) MU=U′
MUв(t) = 1/ t =tв MUт(t) = 2/t =tт По условию tм+tв+tт=4 2/(t-0,5)+ 1/ t +2/t =4 (2t+t-0,5+2t-1)/t(t-0,5)=4 4t2-7t+1,5=0 t1=1,5(=90мин) t2=0,25(=15мин) – не удовлетворяет условию t>0,5 Посчитаем время, которое потратит Василий Разгуляев на каждое развлечение: tм=2(=120 мин) tв=2/3(=40 мин) tт=4/3(=80 мин) ∙ При условии, что Василий сможет покататься на мотоцикле не более получаса: MUм(t)≤0,5 2/(t-0,5)≤0,5 → t ≥ 4,5, что не удовлетворяет условию → → Василий не будет кататься на мотоцикле Посчитаем время, которое он потратит на танцы и выпивку: tв+tт=4 1/ t +2/t =4 t=3/4 → tв = 4/3(=80 мин), tт = 8/3(=160 мин) Ответ: tм=120 мин, tв=40 мин, tт=80 мин; tв =80 мин, tт =160 мин
II способ: U= Uм(t) + Uв(t) + Uт(t) → max 2ln(tм-0,5)+ ln(tв)+ ln(tт²)→ max ∙ Чтобы получить функцию двух переменных, выразим tв из условия tм+tв+tт=4 tв=4- tм-tт 2ln(tм-0,5)+ ln(4- tм-tт)+ ln(tт²)→ max Дифференцируемая функция U достигает экстремума в точке (tм0; tт0), где ее частные производные первого порядка в этой точке равны нулю.
MU(tт)=8-3tт -2tм=0
tм=1,9 tт=1,4 tв=0,7 ∙ Если товарищ согласен одолжить В. Разгуляеву свой не более, чем на 30 минут, Василий не будет кататься на мотоцикле, т.к. Uм(t) = 2ln(t-0,5) и (tм-0,5)>0 по определению логарифма, tм=30мин не удовлетворяет условию
160.Производственная функция фирмы имеет вид :Q=9L2/3 . Труд является единственным фактором производства и нанимается на совершенно конкурентном рынке труда. Средняя производительность труда на этой фирме, при объеме, максимизирующем прибыль в условиях совершенной конкуренции, равна 3. определите максимальную прибыль предприятия, если рыночная цена, продаваемого им товара, равна 2. Решение: Мы знаем, что предельная доходность труда равняется произведению предельного дохода на предельный продукт труда, т.е. MRPL = MR* MPL В условиях совершенной конкуренции предельная выручка равняется цене, т.е. MR = P, следовательно MRPL = P* MPL, т.к. для увеличения прибыли нужно чтобы предельный продукт труда равнялся зарплате, то MRPL =W, значит W = P* MPL Из формулыAPL = TP/L, получим: APL = 9/L^1/3 Если APL =P, то APL= 9/L^(-1/3) = 3 =>L = 27, Q(L=27) = 9*272/3= 81 MPL = Q’(L) = 6L-1/3, приL = 27, MP = 2 W = P* MPL, т.е. W = 2*2 = 4 Pr = (P-AC)*Q, где AC=w/AP = 4/3 Pr = (2-4/3)*81 = 54
Ответ:Pr max = 54
162. Имеется некий инвестиционный проект, который требует в первый период времени (год) вложения 125 млн. руб., во второй — 150 млн. руб., в третий — 160 млн. руб. При этом ставки доходности соответственно составляют 25,30 и 40 % годовых. Какую сумму можно инвестировать сейчас в указанный инвестиционный проект?
Решение: Задача решается по частям, исходя из требований инвестирования и с учетом ставок доходности, используя формулу дисконтирования:
Где
Путем сложения всех трех ответов получим сумму инвестирования сейчас:
Ответ:
163. Две фирмы предлагают проекты строительства дома отдыха. Первая обещает построить дом за 2 года при инвестициях в первый год – 200 млн.руб., во второй год – 300 млн. руб. Вторая фирма обещает построить дом за 3 года при инвестициях в начале каждого года в 90, 180 и 288 млн.руб. соответственно. Определите: • Какой из этих проектов дешевле, если для сравнения использовать ставку дисконтирования = 20%. • Какой из этих проектов дешевле, если для сравнения использовать ставку дисконтирования = 10%. • Уравновешивающую ставку дисконтирования, при которой ни одному из проектов нельзя отдать предпочтение.
Решение: FV= PV(1+ i)n
Дешевле проект с меньшей первоначальной суммой на вкладе → PV = 1) ∙ Посчитаем первоначальную сумму на вкладе для первого проекта при ставке дисконтирования = 20%: По условию инвестиции проходят в начале года → инвестиции за первый год не пересчитываются с учетом ставки дисконтирования PV1=200+ ∙ Посчитаем первоначальную сумму на вкладе для второго проекта при ставке дисконтирования = 20%: PV2=90+ PV1≥ PV2 → второй проект дешевле при ставке дисконтирования = 20% 2) ∙ Посчитаем первоначальную сумму на вкладе при ставке дисконтирования = 10%: PV1=200+ PV2=90+ PV1≤ PV2 → первый проект дешевле при ставке дисконтирования = 10% 3) Необходимо найти i, при которой PV1= PV2 200+ 110i2+340i-58=0 D≈375.7 i=0.16 → Уравновешивающая ставка дисконтирования =16%
165.Спрос на землю задан уравнением: Qd = 100-2R, Q- площадь используемой земли; R- ставка ренты (млн.руб/га). Определите: 1. Равновесную ставку ренты, если площадь доступных земельных угодий 90 га. 2. Какова будет цена одного гектара земли, если ставка банка – 120%. 3. Государство устанавливает максимальный уровень ренты на уровне 3 млн.руб. за гектар. Как эта мера отразится на благосостоянии общества? Решение: Равновесный уровень ренты определим из условия: 100 - 2R = 90, откуда R = 5. Цену одного гектара земли найдем по формуле: Цена земли = Рента/ Ставка банковского процента = 5/1,2 = 4,166 млн. руб. Если государство установит фиксированный уровень ренты, то объем спроса (100-6 = 94) превысит объем предложения земли. Объем чистой экономической ренты, получаемой собственниками земли, сократится с 450 млн. руб. (90 х 5) до 270 млн. руб. (90 х 3). Влияние данного решения на выигрыш покупателя земли оценить количественно невозможно с одной стороны, они выиграют от снижения уровня ренты, с другой стороны — будут страдать и проиграют от дефицита земли. 166. Имеется участок земли размером 5 га. Комбинации используемой площади и получаемого продукта приведены ниже:
• Какая часть земли будет сдана, если рента будет установлена в размере 15 млн.руб./га? • Какая часть земли будет сдана, если рента будет установлена в размере 10 млн.руб./га? • Какую сумму должна составлять рента, чтобы все 5 га были сданы? • Сколько в этом случае будет стоить участок земли, если ставка процента 10% годовых?
Решение: Рента в данном случае является альтернативной стоимостью производительного использования земли ее владельцем. Тогда условие максимизации прибыли примет вид: Рента = Предельный продукт в денежном выражении (MRPL). MRPL = dTRPL/dL, где d - изменение. Представим расчеты в таблице:
Если рента составляет 15 млн. руб., то будут сданы в аренду 3 га; если рента составляет 10 млн. руб., то будут сданы в аренду 2 га. Как следует из данных таблицы, весь участок будет сдан при ренте равной 7 млн. руб. Цену земли рассчитаем по формуле: Цена Земли = Рента/ Процент = 7/ 0,1 = 70 млн. руб. за 1 га. Цена всего участка в этом случае составит 350 млн. рублей.
Ответ: 3 га, 2 га, Р = 350 млн. рублей. 167. Фермер выращивает пшеницу и продает ее на конкурентном рынке по 6 руб./кг. Зависимость объема производства пшеницы от площади используемой земли (производственная функция) задана: Q(X) = 100X-1,5X², где Х – объем использования земли (га)
• Каков максимальный размер ренты, которую может уплатить фермер за пользование землей, если площадь участка 25 га? • Если ставка 5% в год – чему будет равна цена гектара земли?
1. Х=25 rt=MR*MPt – рентная оценка земли ∙ По условию рынок конкурентный → MR=Р=6 ∙ MPt: TP – общее количество продукции = Q MP - предельный продукт = TP′ MP = TP′ = (100X-1,5X²)′=100-3X При X=25 (по условию) MP = 100-3*25 = 25 ∙ rt = 25*6= 150
2. Цена гектара земли – Р: P= R– ставка ренты за один га i - cтавка банковского процента
Из предыдущего пункта rt =150, найдем R: R= rt/ X =150/25=6 P=
Ответ: rt = 150, P=120
169.Производственная функция фирмы, являющейся совершенным конкурентом на рынке готовой продукции, в краткосрочном периоде Q = 200L0,5, где L — количество работников. Цена готовой продукции — 3 долл., а уровень заработной платы — 30 долл. (рынок труда конкурентен). Определите , сколько работников наймет фирма, максимизирующая свою прибыль.
Решение: Мы знаем, что предельная доходность труда равняется произведению предельного дохода на предельный продукт труда, т.е. MRPL = MR* MPL В условиях совершенной конкуренции предельная выручка равняется цене, т.е. MR = P, следовательно MRPL = P* MPL, т.к. для увеличения прибыли нужно чтобы предельный продукт труда равнялся зарплате, то MRPL =W, значит W = P* MPL: MRPL = P* MPL, где MPL = Q’(L) = 100/L0,5 P* Q’(L) = W; 3*100/(L0,5) = 30 L = 100
Ответ: L = 100
170. В краткосрочном периоде производственная функция фирмы, являющейся совершенным конкурентом на рынке готовой продукции, Q = 12L - L²; О ≤ L ≤ 6, где L — количество использованного труда, работников/день; Q — выпуск за день. Цена на продукцию фирмы — 1 долл. за ед. Рынок труда — конкурентный. Выполните задания: 1) начертите функцию спроса фирмы на труд; 2) определите, сколько работников будет нанято по ставке 4 долл./день.
Решение:
В условиях совершенной конкуренции
Выразим количество использованного труда (L)
И получим функцию спроса фирмы на труд
Ответ: 171. Функция полезности работника имеет вид: U = C0,5L0,5, где С — количество потребительских благ; L — свободное время. Ставка заработной платы в номинальном выражении равна 20 руб./ч. Величина дохода помимо заработной платы составляет 80 руб./день. Уровень цен на потребительские блага равен 2. Определите объем предложения труда работником в день. Решение: ∙ I = заработная плата + дополнительный доход ∙ Заработная плата=w(24-H0) – дневной доход, где (24-H0) – рабочее время, H0 – свободное время, w – ставка заработной платы ∙ I = P*C= w(24-H0)+Iдоп ∙ C = C = ∙ Предельная норма замещения MRSLC = MUL=C0.5/2L0.5 MUC= L0.5/2 C0.5
(C0.5/2L0.5)*(2 C0.5/ L0.5)=C/L=10 ∙ 280-10L=10L L=14 C=140 ∙ N=24-14=10 Ответ: объем предложения труда работником в день =10
173.Фирма платит работнику 2 руб./ч за работу в течение первых 40 ч в неделю и 3 руб./ч за сверхурочные работы. В настоящее время работник трудится 50 ч/неделю. Фирма предлагает ему перейти на новую систему оплаты по постоянной ставке заработной платы на уровне 2,2 руб./ч независимо от отработанного времени. Работник утверждает, что при новой системе оплаты труда его заработок сократится. Руководство же фирмы заявляет, что его благосостояние повысится. Определите, с какой из двух сторон вы согласны. Решение: tgL = - 2 , tgB = - 3 , tgY = -2,2. Бюджетное ограничение 1: I = 464 - 3H при О <H< 128; I = 2*( 168 - H ) при 128 <H< 168. Бюджетное ограничение 2: I = 2,2(168 - H). Бюджетное ограничение 2 проходит через точку первоначального равновесия (118; 110), в которой кривая безразличияU1 касается бюджетного ограничения 1, значит, бюджетное ограничение 2 является секущей изначальной кривой безразличияU1.Следовательно, новая кривая безразличия U2, которая касается бюджетного ограничения 2, лежит выше U1.Поэтому благосостояние работника увеличится, хотя он станет зарабатывать меньше. Следовательно, обе стороны правы. I 464 1
110 U2
80 L 168 H
174. Условия спроса на конкурентном рынке труда характеризуются уравнением: wd = 10 - 1/5 L, а предложения: ws= 2 + 1/450L², где w — почасовая ставка зарплаты; L — количество человеко-часов за данный промежуток времени. Найдите экономическую ренту работников. Решение: То, что на товарных рынках называют излишком производителя (или продавца), на факторных рынках называют экономической рентой владельца фактора.
Умножим на -450 каждое слагаемое
При L равном 0 функция предложения примет свое минимальное значение Ws= 2 + 1/450*0=2 Экономическая рента (излишек производителя) равна площади закрашенного треугольника S=
Ответ:экономическая рента работников равна 30 ден. ед.
175. В краткосрочном периоде производственная функция фирмы: Q(Li) = 16Li - Li² , где Li — объем труда, используемого данной фирмой, О ≤ Li ≤ 8. В отрасли действует 10 идентичных конкурентных фирм. Отраслевой спрос на выпускаемую продукцию задан функцией: Р = 10 - Q, где Q — отраслевой объем производства. Труд продается и покупается на конкурентном рынке. Выведите обратную функцию отраслевого спроса на труд.
Пусть: Q = L = Поскольку все фирмы идентичны, то Q=nQi, L=nLi
Решение в данной системе: Ответ: w =160 – 258L + 4,8L2 – 0,02L3
177.Фирма — совершенный конкурент на рынке продукции покупает труд на совершенно конкурентном рынке труда. Цена на продукцию фирмы равна 60. Рыночная цена аренды капитала равна 30. Производственнаяфункция фирмы Q = (KL)0,5. Определите цену, по которой фирма будет покупать труд в долгосрочном периоде. Решение: Мы знаем, что предельная доходность труда равняется произведению предельного дохода на предельный продукт труда, т.е. MRPL = MR* MPL В условиях совершенной конкуренции предельная выручка равняется цене, т.е. MR = P, следовательно MRPL = P* MPL, т.к. для увеличения прибыли нужно чтобы предельный продукт труда равнялся зарплате, то MRPL =W, значит W = P* MPL: MPL = Q’(L) = 0,5KL-0,5 W= P*0,5*(K/L)0,5
При P = 60, W = 30К0,5/L0,5
r = P*MPK;
r = 0,5p(L/K)0,5;
ПриP= 60, r = 30L0,5/K0,5 =>K0,5= 30L0,5/ r;
W = 30К0,5/L0,5 = 30*30L0,5/r* L0,5 = 900/r = 30
Ответ:фирма будет покупать труд в долгосрочном периоде по цене, равной 30.
179.На рассмотрение предлагается два инвестиционных проекта (см. табл.). Ставка процента равна 10% годовых.
На основе метода дисконтирования определите, какой проект предпочтительнее.
Решение: Предпочтительнее будет проект с большей чистой приведённой стоимостью – NPV - суммой дисконтированных значений потока платежей, приведённых к сегодняшнему дню. Чтобы посчитать NPV, необходимо сравнить текущую стоимость инвестиционных затрат (Io) с текущей стоимостью доходов (PV). Разность между ними составляет чистую текущую стоимость доходов (NPV) NPV = PV – Io
∙ Посчитаем чистую приведенную стоимость первого проекта:
Io1= PV1= NPV1 = PV1 – Io1 NPV1 ≈105,57
∙ Посчитаем чистую приведенную стоимость второго проекта: Io2= PV2= NPV2 = PV2 – Io2 NPV2 ≈139,4
Ответ: второй проект предпочтительнее, т.к. NPV1≤ NPV2
12 |




 ∙
∙  Uм(t) = 2ln(t-0,5) t-0,5>0 t>0,5
Uм(t) = 2ln(t-0,5) t-0,5>0 t>0,5 MUм(t) = 2/(t-0,5) = tм
MUм(t) = 2/(t-0,5) = tм MU(tм)=8,5-2 tт -3tм=0
MU(tм)=8,5-2 tт -3tм=0 tт =
tт = 
 5tм = 9,5
5tм = 9,5
 - сегодняшняя ценность;
- сегодняшняя ценность; -ценность через n периодов(лет);
-ценность через n периодов(лет); -ставка дисконтирования (доходность, банковский процент);
-ставка дисконтирования (доходность, банковский процент);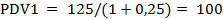 млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб. млн. руб.
млн. руб.
 =450
=450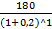 +
+  =440
=440 ≈472,7
≈472,7 +
+  ≈491,6
≈491,6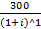 =90+
=90+  +
+ 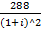

 *100%
*100% *100%=120
*100%=120

 )
)






 = 280-10L
= 280-10L =
=  = 10
= 10 369,6 2
369,6 2 U1
U1








 —отраслевое предложение (равное спросу);
—отраслевое предложение (равное спросу); – отраслевой спрос на труд.
– отраслевой спрос на труд. Обратная функция отраслевого спроса на труд находится из решения следующей системы уравнений:
Обратная функция отраслевого спроса на труд находится из решения следующей системы уравнений: PRmax = pQi wLi – FC (1)
PRmax = pQi wLi – FC (1) (7)
(7) (8)
(8) )))
)))  =nφ(n(f (
=nφ(n(f (  )))∙
)))∙ 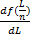
 )2)(16/10 – 1/102∙2L) = 160 – 258L + 4,8L2 – 0,02L3
)2)(16/10 – 1/102∙2L) = 160 – 258L + 4,8L2 – 0,02L3 +
+  +
+  ≈868,5
≈868,5 +
+  +
+  ≈974,07
≈974,07 +
+  +
+  ≈828,7
≈828,7 +
+  ≈968,1
≈968,1