 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Кинетическая энергия механической системы 12
Кинетическая энергия механической системы (К) – это энергия механического движения этой системы. Любое движущееся тело обладает кинетической энергией. Кинетическая энергия зависит только от массы и скорости тела и равна:
Сила, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении
Тело массой m, движущееся со скоростью
Откуда
Кинетическая энергия является функцией состояния системы, всегда положительна, неодинакова в разных системах отсчета. Потенциальная энергия Потенциальная энергия (W) – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам. 1. Потенциальная энергия тела массы m на высоте h:
2. Потенциальная энергия упругодеформированного тела:
Единица кинетической и потенциальной энергии – Джоуль (Дж) Потенциальное поле – поле, в котором работа, совершаемая силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Силы, действующие в таких полях, называются консервативными. Консервативной (потенциальной) называют силу, работа которой определяется только начальным и конечным положениями тела и не зависит от формы пути. Консервативными силами являются силы тяготения, упругости. Все центральные силы консервативны. Если же работа, совершаемая силой, зависит от формы траектории, то такая сила называется диссипативной (например, сила трения). Работа консервативных сил при элементарном изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии.
Поскольку
Вектор
Закон сохранения энергии Полная механическая энергия системы – энергия механического движения и взаимодействия, равная сумме кинетической и потенциальной энергий Закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не меняется со временем
Это фундаментальный закон природы. Он является следствием однородности времени – инвариантности физических законов относительно выбора начала отсчета времени. Механические системы, на которые действуют только консервативные силы (внутренние и внешние), называются консервативными системами. В консервативных системах полная механическая энергия остается постоянной. Могут лишь происходить превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах, так что полная механическая энергия остается неизменной. В системе, в которой кроме консервативных сил действуют и диссипативные силы, полная механическая энергия не сохраняется. Такие системы называются диссипативными. При «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида (например, тепловой). Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одной формы в другую. В этом заключается физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.
Соударения Удар (соударение) – столкновение дух или более тел, при котором взаимодействие длится очень короткое время. Центральный удар – удар при котором тела до удара движутся по прямой, проходящей через их центры масс. Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. При абсолютно упругом ударе сохраняются импульс и механическая энергия. Рассмотрим прямой центральный абсолютно упругий удар двух шаров массами m1 и m2. Обозначим скорости шаров до удара
Рисунок 3 – Абсолютно упругое соударение шаров, двигающихся на встречу друг другу
Закон сохранения импульса в векторном виде:
Закон сохранения энергии:
. Отсюда
(1.22)
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.
Рисунок 4 – Абсолютно неупругое соударение шаров.
При абсолютно неупругом ударе выполняется только закон сохранения импульса:
Или в проекциях на ось х:
Скорость после удара равна:
Механическая энергия при неупругом ударе не сохраняется: вследствие деформации часть кинетической энергии переходит во внутреннюю энергию тел. Это уменьшение равно:
Вывод рабочей формулы Используя баллистический метод, получим формулу для определения скорости шаров в момент прохождения положения равновесия. В этом методе мерой скорости служит величина угла отброса, рассчитываемая по круглой шкале. В точке А (рисунок 5) шарик обладает потенциальной энергией равной
Систему маятник-Земля рассматриваем как замкнутую, пренебрегая трением в подвесе маятника и сопротивлением воздуха. При перемещении шарика из положения А в положение С его потенциальная энергия перейдет в кинетическую.
Рисунок 5 – Отклонение шарика от положения равновесия. Откуда
Используя соотношения в прямоугольном треугольнике и тригонометрическую формулу
и подставим в выражение для скорости ( ) Получим
Порядок выполнения работы 1 Ознакомьтесь с лабораторной установкой. 2 Измерьте и запишите длину подвеса l в таблицу 1. Таблица 1– Результаты измерений
Упражнение 1 Изучение упругого соударения шаров одинаковой массы. 1 Поместите шары одинаковой массы на подвесы ( 2 Отклоните первый на угол 3 Определите скорости первого 4 Отпустите шары. Определите значения углов 5 Определите скорости первого 6 Проверьте выполнение закона сохранения импульса при упругом ударе Выберите направление координатной оси, найдите проекции скоростей 7 Рассчитайте относительное отклонение в % по формуле:
Упражнение 2 Изучение упругого соударения шаров разной массы (. 1 Поместите на подвесы шары разной массы ( 2 Отклоните первый на угол 3 Определите скорости первого 4 Отпустите шары. Определите значения углов 5 Определите скорости первого 6 Проверьте выполнение закона сохранения импульса при упругом ударе Выберите направление координатной оси, найдите проекции скоростей 7 Рассчитайте относительное отклонение в % по формуле:
Упражнение 3 Изучение упругого соударения шаров разной массы (. 1 Поместите на подвесы шары разной массы ( 2 Отклоните первый на угол 3 Определите скорости первого 4 Отпустите шары. Определите значения углов 5 Определите скорости первого 6 Проверьте выполнение закона сохранения импульса при упругом ударе Выберите направление координатной оси, найдите проекции скоростей 7 Рассчитайте относительное отклонение в % по формуле: 12 |



 . (1.11)
. (1.11) (1.12)
(1.12) , обладает кинетической энергией
, обладает кинетической энергией . (1.13)
. (1.13) (1.14)
(1.14) (1.15)
(1.15) (1.16)
(1.16) (1.17)
(1.17) , то
, то  , отсюда
, отсюда (1.18)
(1.18) называется градиентом скалярной функции W и характеризует быстроту изменения скалярной функции в данном направлении.
называется градиентом скалярной функции W и характеризует быстроту изменения скалярной функции в данном направлении. .
. . (1.19)
. (1.19) и
и  , после удара -
, после удара -  и
и  .
.
 . (1.20)
. (1.20) (1.21)
(1.21)


 . (1.23)
. (1.23) (124)
(124) (1.25)
(1.25)
 (2.1)
(2.1)
 (2.2)
(2.2)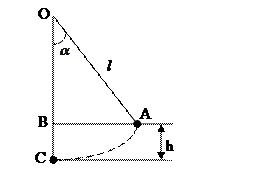
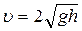 (2.3)
(2.3) ,выразим высоту h через длину нити l и угол
,выразим высоту h через длину нити l и угол 
 (2.4)
(2.4) (2.5)
(2.5)









 ). Запишите значения масс шаров в талицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости линейки.
). Запишите значения масс шаров в талицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости линейки. , для нахождения
, для нахождения  .
. , где
, где  - импульс системы до удара,
- импульс системы до удара,  - импульс системы после удара.
- импульс системы после удара.
 ). Запишите значения масс шаров в талицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости линейки.
). Запишите значения масс шаров в талицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости линейки.
 ). Запишите значения масс шаров в талицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости линейки.
). Запишите значения масс шаров в талицу 1. Убедитесь, что центры масс шаров находятся на одинаковой высоте в плоскости, параллельной плоскости линейки.