 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Формирователь модулирующих символов 12
Решение: 1. Изобразить сигнальное созвездие для вида модуляции – КАМ-16 (квадратурная амплитудная модуляция) рис. 3.4.1..
Рис. 3.4.1. КАМ-16 2. Изобразить график реализации 3. В соответствии с сигнальным созвездием модулятора КФМ-4 изобразить для входной реализации Реализацию
можно представить в следующей аналитической форме
где
где Последовательность КС из 16 символов: 1011 0000 0000 0011 Процессы
где
где
Рис. 3.4.2. Реализации для КАМ-16 4. Написать аналитические выражения для корреляционной функции
5. Написать аналитические выражения для корреляционных функций
Рис. 3.4.3. график корреляционной функции
Рис. 3.4.4. график функции спектральной мощности 6. Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала. Теорема Хинчина — Колмогорова (также известная как Теорема Винера — Хинчина и иногда как Теорема Винера — Хинчина — Эйнштейна) утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей автокорреляционной функции Теорема удобна для анализа линейных стационарных систем, где входные и выходные значения не интегрируемы в квадратурах, из-за чего преобразований Фурье не существует. Как следствие, преобразование Фурье автокорреляционной функции выходного сигнала ЛСС-системы равно произведению преобразования Фурье автокорреляционной функции входного сигнала системы на квадрат модуля преобразования Фурье её импульсной характеристики. Это выполняется даже когда преобразований Фурье входных и выходных сигналов не существует, из-за того что они не интегрируемы. Поэтому входные и выходные параметры не могут быть прямо связаны преобразованием Фурье импульсной передаточной функции. Из того, что преобразование Фурье автокорреляционной функции сигнала есть спектр мощности сигнала, следует, что спектр мощности выходного сигнала равен произведению спектра мощности входного и передаточной функции системы. Это следствие используется в нахождении спектра мощности параметрическим методом.
Модулятор В состав модулятора входят блоки-перемножители, инвертор и сумматор, на выходе которого получаем сигнал заданного вида модуляции КАМ-16. Решение: 1. Построить графики гармонических колебаний 2. На этих же интервалах
3. На этих же интервалах I(t)={-h,h,h,-h} q(t)={-3h,h,h,-3h} – значения I(n) и Q(n) на промежутке n=0…3.
Рис. 3.5.1. графики сигналов 4. Написать аналитические выражения для корреляционных функций
5. Написать аналитические выражения для корреляционной функции сигнала
Строим графики функций
Рис. 3.5.2. график функции корреляции на выходе сумматора
Рис. 3.5.3. график функции спектральной плотности мощности
Непрерывный канал В КР непрерывный канал (НК) рассматривается практически по той же методике, как в предыдущей КР [14].[1] Передача сигнала
где
Требуется: 1. Определить минимально необходимую ширину полосы частот непрерывного канала
2. Определить мощность помехи
РП=2,542 10-5 3. Определить
4. Рассчитать пропускную способность
5. Оценить эффективность использования пропускной способности непрерывного канала.
Демодулятор Требуется: 1. Изобразить структурную схему когерентного демодулятора, оптимального по критерию максимального правдоподобия для КАМ -16.
Рис. 3.7.1 структурная схема 2. Написать алгоритмы работы решающих устройств РУ в составе когерентного демодулятора.
Формирователь квадратур (ФК) состоит из двух перемножителей (фазовых детекторов), двух фильтров нижних частот (ФНЧ) и фазовращателя опорного колебания на 90 (ФВ). Фильтр основной селекции демодулятора может быть реализован как на промежуточной частоте, так на видеочастоте, то есть это может быть как фильтр УПЧ, так и фильтры низкой частоты ФК. Частота дискретизации сигналов в АЦП равна удвоенной тактовой частоте входного сигнала: fд= 2fт. Формирование на выходе АЦП двух отсчетов сигнала за длительность одного информационного символа Tс= 1/fт необходимо для работы временного дискриминатора УТС. Устройство выделения информации (УВИ) содержит делитель тактовой частоты на 2 (ДЧ), два устройства (делителя на 2), осуществляющих прореживание сигнала (на выходы этих устройств поступает каждый второй отсчет входных сигналов), два решающих устройства (РУ), которые формируют выходные данные квадратурных каналов, и дифференциальный декодер. Разрядность данных на выходе РУ определяется позиционностью КАМ-М сигнала M и равна (log2M)/2. В некоторых случаях при реализации демодулятора сигнал на временной дискриминатор УТС и на амплитудный детектор АРУ снимается с выходов формирователя квадратур. При этом устройства тактовой синхронизации и автоматической регулировки усиления являются полностью аналоговыми. В состав УВИ можно добавить корректор межсимвольных искажений, который подключают к выходам АЦП (Tс/2-интервальный корректор) или к выходам устройств прореживания (Tс-интервальный корректор).
3. Определить вероятности ошибок на выходах РУ1 и РУ2 при определении значений символов
где
4. На четырех символьных интервалах длительностью На вход демодулятора поступает последовательность импульсов: i(t)={-h,h,h,-h} q(t)={-3h,h,-3h} g2=101 Генератор В момент окончания символьного интервала длительностью Получаем последовательность импульсов на РУ1: {-h,h,h,h}; Получаем последовательность импульсов на РУ2: {h,-h,h,h}; Выбираем максимальное из каждой пары, строим последовательность импульсов рис. 3.7.2.:
Рис. 3.7.2. сигналы на выходах РУ1 и РУ2 5. Определить вероятности ошибок на выходах РУ1 и РУ2 для значений сигналов
6. Определить вероятности ошибок на выходе преобразователя параллельного кода в последовательный код (ФМС) для заданных параметров сигналов
Выбираем из таблицы 3 соответствующую формулу, получаем: рош=8,834 10-3 7. Определить среднюю вероятность ошибки на выходе преобразователя.
Декодер 1. Изучить алгоритм сверточного декодирования по методу Витерби [7, с. 23–37]. В этом методе декодирования вместо кодового дерева используется решетчатая структура. Было установлено, что алгоритм Витерби является методом динамического программирования (которое уже было известно в то время), примененным к сверточным кодам. Сверточное кодирование, применяемое вместе с декодированием Витерби, в настоящее время стало одним из наиболее широко используемых на практике методов исправления ошибок. С целью реализации устойчивой работы кодера при сверточном декодировании периодически проводят очистку (промывку) регистра сдвига кодера от информационных символов путем подачи на кодер некоторого количества нулевых символов (не информационных). Эта операция называется периодическим отбрасыванием. Следующая партияинформационных символов поступает на кодер, когда все ячейки регистра сдвига находятся в нулевом состоянии, т.е. в состоянии а=00. Обозначим: 1) 2) 3) С учетом сказанного рассмотрим алгоритм сверточного декодирования Витерби с использованием решетчатой диаграммы. Декодирование начинается в момент 2. Используя табл. 2, написать численные значения принятых кодовых символов (ПКС). Выписанные численные значения образуют последовательность
Требуется: 1. Построить решетчатую диаграмму декодера последовательности Ошибка в 1-м символе. Следовательно. Получаем последовательность:
Решетчатая диаграмма декодера отличается от решетчатой диаграммы кодера тем, что ребрам этих решеток соответствуют разные обозначения. Числа над ребрами решетки декодера определяются, как расстояния Хемминга между двумя символами принятой последовательности
Рис. 3.8.1. Решеточная диаграмма декодера 2. Построить диаграммы выживших путей от момента времени Выделим часть пути до момента времени t=3.
Рис. 3.8.2. часть решеточной диаграммы Определим по диаграмме на рис.3.8.2 метрику путей по Хеммингу, исходящих из одной точки и приходящих в узлы e,f,g,h. В точку e: 1+1=2 В точку f: 1+1=2 В точку g: 0+1=1 В точку h: 1+1=2 Выбираем наиболее короткие пути как выжившие, выделим их желтым цветом.
Рис. 3.8.3. выжившие пути 3. Перенести один выживший путь от момента времени
Проследить по диаграмме, что ошибка, отмеченная крестиком, исправлена. 4. По выжившему пути, перенесенному на решетчатую диаграмму кодера, определить соответствие информационным символам Декодер принимает решение, что на интервале от
от момента
Список использованной литературы
1. Зюко, А. Г. Теория передачи сигналов / А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Л. М. Финк. – Изд. 2-е, перераб. и дополнен. – М. : Радио и связь, 1986. – 304 с. 2. Зюко, А. Г. Теория электрической связи : учебник для вузов / А. Г. Зюко, Д. Д. Кловский, В. И. Коржик, М. В. Назаров. – М. : Радио и связь, 1998. 3. Скляр, Бернард. Цифровая связь. Теоретические основы и практическое применение : пер. с англ. / Бернард Скляр. – Изд. 2–2, испр. – М. : Издательский дом «Вильямс», 2003. – 1104 с. 4. Кларк, Дж. Кодирование с исправлением ошибок в системах цифровой связи / Дж. Кларк, мл. Дж. Кейн : пер. с англ. С. И. Гельфонда ; под ред. Б. С. Цыбакова. – М. : Радио и связь, 1987. – Вып. 28. – 392 с. 5. Григоровский, Л. Ф. Теория электрической связи. Модели сигналов и методы их преобразования в системах связи : учеб. пособие / Л. Ф. Григоровский, В. И. Коржик, В. Г. Красов, В. Ф. Кушнир. – Л. : ЛЭИС. – 1990. 6. Тихонов, В. И. Статистическая радиотехника / В. И. Тихонов. – Изд. 2-е, перераб. и дополнен. – М. : «Радио и связь», 1982. – 624 с. 7. Куликов, Л. Н. Теория электрической связи. Основы сверточного кодирования : учеб. пособие / Л. Н. Куликов, М. Н. Москалец. – СПб., 2006.
Оглавление ВВЕДЕНИЕ.. 2 2. СИСТЕМА ЦИФРОВОЙ СВЯЗИ.. 3 3. ИСХОДНЫЕ ДАННЫЕ. 5 3.1. Источник сообщения. 6 3.2. Аналого-цифровой преобразователь. 10 3.3. Кодер. 13 3.4. Формирователь модулирующих символов. 15 3.5. Модулятор. 21 3.6. Непрерывный канал. 25 3.7. Демодулятор. 27 3.8. Декодер. 32 4. Список использованной литературы.. 37
12 |




 случайного процесса
случайного процесса 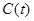 с выхода блока сверточного кодера (К) на входе блока ФМС на первых 16 бинарных интервалах длительностью
с выхода блока сверточного кодера (К) на входе блока ФМС на первых 16 бинарных интервалах длительностью  . Написать аналитическое выражение для случайного процесса
. Написать аналитическое выражение для случайного процесса  графики реализаций
графики реализаций  и
и  на выходе блока ФМС случайных процессов
на выходе блока ФМС случайных процессов  и
и  на символьных интервалах длительностью
на символьных интервалах длительностью  Написать аналитические выражения для случайных процессов
Написать аналитические выражения для случайных процессов 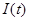 и
и 
 случайного процесса
случайного процесса

 – прямоугольный импульс длительностью
– прямоугольный импульс длительностью  ,
,

 – прямоугольный импульс такой же формы, как
– прямоугольный импульс такой же формы, как  , если
, если  , или влево, если
, или влево, если  ;
;  – численный коэффициент, являющийся реализацией случайной величины
– численный коэффициент, являющийся реализацией случайной величины  на
на  -интервале
-интервале  и
и  можно представить в виде
можно представить в виде ;
;  ,
, – прямоугольный импульс длительностью
– прямоугольный импульс длительностью  (рис. 3.4.2., б);
(рис. 3.4.2., б);  – символьный интервал;
– символьный интервал; 

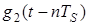 – прямоугольный импульс такой же формы, как импульс
– прямоугольный импульс такой же формы, как импульс  , но сдвинутый вправо относительно импульса
, но сдвинутый вправо относительно импульса  , или влево, если
, или влево, если  ;
;  и
и  – независимые случайные величины, заданные на символьном интервале с номером
– независимые случайные величины, заданные на символьном интервале с номером  , которые согласно сигнальному созвездию (рис. 3.4.1) принимают два дискретных значения
, которые согласно сигнальному созвездию (рис. 3.4.1) принимают два дискретных значения  ,
,  , 3h, -3h с вероятностью 0,25 каждое, т.е.
, 3h, -3h с вероятностью 0,25 каждое, т.е.

 и
и  случайных процессов
случайных процессов 
 и спектральной плотности мощности
и спектральной плотности мощности  входного случайного процесса
входного случайного процесса 
 =
= 

 .
. и
и  , спектральных плотностей мощности
, спектральных плотностей мощности  и
и 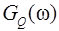 случайных процессов
случайных процессов  Построить графики этих функций.
Построить графики этих функций.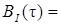


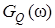





 и
и  на четырех символьных интервалах
на четырех символьных интервалах  (
(  ). При этом на символьном интервале длительностью
). При этом на символьном интервале длительностью  укладывается два периода частоты
укладывается два периода частоты  .
.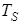 нарисовать графики сигналов
нарисовать графики сигналов ;
; ;
;
 на выходе сумматора в квазигармонической форме, выделив из полученной суммы четыре слагаемых с номерами
на выходе сумматора в квазигармонической форме, выделив из полученной суммы четыре слагаемых с номерами  . Фазы
. Фазы  определять по сигнальному созвездию.
определять по сигнальному созвездию.

 ,
,  для случайных сигналов
для случайных сигналов  и
и  на выходах перемножителей, где
на выходах перемножителей, где  случайная фаза с равномерной плотностью вероятности на интервале
случайная фаза с равномерной плотностью вероятности на интервале  . Случайная фаза
. Случайная фаза  и
и 
 .
.

 .
. и для спектральной плотности мощности
и для спектральной плотности мощности  сигнала
сигнала  КФМ-4 на выходе сумматора. Построить графики этих функций.
КФМ-4 на выходе сумматора. Построить графики этих функций.
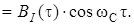
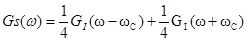


 происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи типа гауссовского белого шума. Сигнал на выходе такого канала имеет вид
происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии аддитивной помехи типа гауссовского белого шума. Сигнал на выходе такого канала имеет вид
 – коэффициент передачи канала. Для всех вариантов
– коэффициент передачи канала. Для всех вариантов  . Односторонняя спектральная плотность мощности помехи равна
. Односторонняя спектральная плотность мощности помехи равна  = 1.85 10-7
= 1.85 10-7 .
.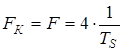 =0.035
=0.035 на выходе канала.
на выходе канала.
 F=Ts+fc a=2
F=Ts+fc a=2 среднюю мощность сигнала
среднюю мощность сигнала  =1?145 107
=1?145 107 =1312 105
=1312 105 =5.162 109
=5.162 109 (за секунду) непрерывного канала.
(за секунду) непрерывного канала. =1.168
=1.168 , где Н’=2fв 1,443 L
, где Н’=2fв 1,443 L
 и
и  , равных –h, h, -3h, 3h:
, равных –h, h, -3h, 3h: =
=  =
=  =
=  ;
; =
=  =
=  =
=  ,
,



 =
= 




 =
= 





 =
= 




 =
= 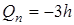


 (разд. 4.5).
(разд. 4.5). вырабатывает сигнал
вырабатывает сигнал  на интервале с номером
на интервале с номером  , а на интервале с номером
, а на интервале с номером  – сигнал
– сигнал  .
. решающее устройство (РУ1) сравнивает 2 входных напряжения равенств и выбирает из них максимальное, тем самым реализуя правило принятия решения.
решающее устройство (РУ1) сравнивает 2 входных напряжения равенств и выбирает из них максимальное, тем самым реализуя правило принятия решения.
 и
и  , равных
, равных 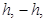 при условии
при условии 




 - последовательность информационных символов, поступивших на вход кодера;
- последовательность информационных символов, поступивших на вход кодера; - последовательность кодовых символов с выхода кодера, которая передавалась по каналу;
- последовательность кодовых символов с выхода кодера, которая передавалась по каналу; - принятая последовательность, полученная с выхода демодулятора и поступившая на вход декодера.
- принятая последовательность, полученная с выхода демодулятора и поступившая на вход декодера. . В результате очистки кодера между сообщениями будем считать, что декодер находится в начальном состоянии а=00.
. В результате очистки кодера между сообщениями будем считать, что декодер находится в начальном состоянии а=00. , соответствующую последовательности
, соответствующую последовательности 

 =0*1 10 11 00 00 00 00 00 11 {1,1,2,0,0,0,0,0,2}
=0*1 10 11 00 00 00 00 00 11 {1,1,2,0,0,0,0,0,2}
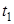 до момента времени
до момента времени 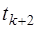 по аналогии с решетчатыми диаграммами [7, рис. 11–17], когда от момента
по аналогии с решетчатыми диаграммами [7, рис. 11–17], когда от момента  до момента
до момента  выживает только один путь.
выживает только один путь.
 до момента t5 с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы, которые поступали на вход сверточного кодера и передавались по каналу связи от момента
до момента t5 с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы, которые поступали на вход сверточного кодера и передавались по каналу связи от момента  до момента
до момента  , соответствующие принятым кодовым символам с учетом исправленной ошибки.
, соответствующие принятым кодовым символам с учетом исправленной ошибки.
 Рис.3.8.4. наложение диаграмм.
Рис.3.8.4. наложение диаграмм.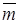 , которые поступали на вход сверточного кодера, принятых кодовых символов с учетом исправленной ошибки.
, которые поступали на вход сверточного кодера, принятых кодовых символов с учетом исправленной ошибки.