 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Действия с одночленами и многочленами.
Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена и полученные произведения сложить: а · (b + c - d) = ab + ac – ad. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить: (а + b)(c - d) = ac – ad + bc - bd Чтобы разделить многочлен на одночлен нужно каждый член многочлена разделить на этот одночлен и полученные результаты сложить.Пр. (5mn - 0,4mc) : 2 m = 2,5n – 0,2c Практическая часть | Уметь выполнять простейшие действия со степенью | Уметь выполнять простейшие действия с одночленами и многочленами | Приводить подобные члены в многочлене | 1) а3·а5; 2) 521: 519; 3) (а8)5; 4)  ; 5) (а2в)3; 6) 54·74; 7) ; 5) (а2в)3; 6) 54·74; 7)  . . | 8) (2p)(-3c2); 9) (-  а3хy3)( а3хy3)(  ах2y); 10) (3в2)4; 11) (-3х2y4)3; 12) 2(3a2 – 4a +8); 13) 7ав(2а +3в); 14) 5а2в(15в + 3); 15) 7(4х + 3) – 6(5 + 7х); ах2y); 10) (3в2)4; 11) (-3х2y4)3; 12) 2(3a2 – 4a +8); 13) 7ав(2а +3в); 14) 5а2в(15в + 3); 15) 7(4х + 3) – 6(5 + 7х); | 16) 6n(2t -3n) -3t(3t –2n); 17) (а + 2)(а + 3); 18) (а – 10)(- а – 2); 19) (-6х):(2х); 20) (10pq):(6q); 21) (12а + 6):3; 22) (4х2 – 3ху):х; | 23) 11х2 + 4х – х2 - 4х; 24) х2 + 3у2 + 4х2 – у2; 25) (13x - 11y) – (-15x + 10y); | | Упрощать выражения | | 26) 5х – (2х – 3у); 27) (х – 3)х – (4 – х) + 3х; 28) (3в + с2 – d) – (c2 – 2d) 29) P + Q , если P = 5a2 + b, Q = - 4а2 - b |
Образовательный минимум по геометрии за II четверть. Теоретическая часть. Треугольники. Понятие треугольника.Соединим три точки А, В, С, не лежащие на одной прямой. отрезками АВ, ВС, СА. Треугольником называют часть плоскости вместе с данными отрезками. Определение: периметром треугольника называют сумму длин всех его сторон. | Виды треугольников Остроугольный - Прямоугольный - Тупоугольный - все углы острые. один из углов прямой. Один из углов тупой. |
В Определение: Перпендикуляр, опущенный из вершины треугольника на прямую, Всодержащую противолежащую сторону, называют высотой треугольника. <ВКС = 90°. ВК – высота. Определение: Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называют медианой треугольника. А М N K C АМ = МС, ВМ –медиана. Определение: отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называют биссектрисой треугольника. <ABN = <NBC, BN – биссектриса. Равнобедренный треугольник | Определение | Свойства | | Треугольник, у которого две стороны равны, называют равнобедренным. АС – основание ΔАВС, АВ, ВС – боковые стороны. | 1. Теорема: В равнобедренном треугольнике углы при основании равны. B Дано:ΔАВС, АВ = ВС. Доказать:<А = <С. Доказательство:рассмотрим ΔАВС. 1) Пусть АD –биссектриса ΔАВС; D 2) ΔАВD = ΔDВС (по I-му); A C 3) <А = <С. D 2.Биссектриса треугольника, проведённая из угла при вершине, является медианой и высотой | | Треугольник, у которого все стороны равны называется равностоорнним. | Признаки равенства треугольников | I признак по двум сторонам и углу между ними | II признак по стороне и двум прилежащим углам | III признак по трем сторонам |  = =  |  = =  | 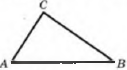 = =  | Практическая часть Перпендикулярные прямые. 1. На рисунке   . Найдите < ABF. . Найдите < ABF. | Равнобедренный треугольник, его свойства и признаки. 7. Периметр равнобедренного треугольника равен 28см, а боковая сторона 10 см.Найдите основание треугольника. 8. Найдите стороны равнобедренного треугольника, периметр которого равен 54 см, а основание в 4 раза меньше боковой стороны. 9. На рисунке  МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 10. Прямая пересекает стороны угла А в точках В и С МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 10. Прямая пересекает стороны угла А в точках В и С  так, что АВ = АС. Докажите, что <1=<2. 11. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. так, что АВ = АС. Докажите, что <1=<2. 11. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. | | Периметр треугольника. Медиана, биссектриса и высота треугольника. 2. С помощью линейки и транспортира постройте медиану, биссектрису и высоту данных треугольников.  3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. 3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. | | Первый и второй признаки равенства треугольников. 4. На рисунке 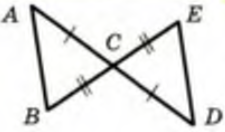 АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 5. Дано: АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 5. Дано: 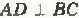 ВD = CD. ВD = CD.  Докажите, что АВ = АС. 6. На рисунке Докажите, что АВ = АС. 6. На рисунке 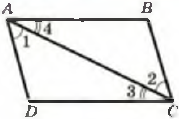 <1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. <1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. | | Третий признак равенства треугольников. 12. На рисунке  АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 13. На рисунке АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 13. На рисунке 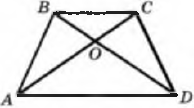 АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный. АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный. | | Список литературы.
1. Алимов Ш.А., Колягин Ю.М. Алгебра 7. – М. «Просвещение» 2010. 2. Атанасян Л.С. Геометрия 7 – 9. М. «Просвещение» 2010. 3. Мерзляк Г.А. Геометрия 7.-М. «Вентана-Граф» 2013. 4. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по алгебре для 7 класса. Харьков. «Гимназия» 2010. 5. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по геометрии для 7 класса. Харьков. «Гимназия» 2010.
|




 ; 5) (а2в)3; 6) 54·74; 7)
; 5) (а2в)3; 6) 54·74; 7)  .
.  а3хy3)(
а3хy3)(  ах2y); 10) (3в2)4; 11) (-3х2y4)3; 12) 2(3a2 – 4a +8); 13) 7ав(2а +3в); 14) 5а2в(15в + 3); 15) 7(4х + 3) – 6(5 + 7х);
ах2y); 10) (3в2)4; 11) (-3х2y4)3; 12) 2(3a2 – 4a +8); 13) 7ав(2а +3в); 14) 5а2в(15в + 3); 15) 7(4х + 3) – 6(5 + 7х);  =
= 
 =
= 
 =
= 

 . Найдите < ABF.
. Найдите < ABF. МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 10. Прямая пересекает стороны угла А в точках В и С
МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 10. Прямая пересекает стороны угла А в точках В и С  так, что АВ = АС. Докажите, что <1=<2. 11. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный.
так, что АВ = АС. Докажите, что <1=<2. 11. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный.  3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника.
3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 5. Дано:
АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 5. Дано:  ВD = CD.
ВD = CD.  Докажите, что АВ = АС. 6. На рисунке
Докажите, что АВ = АС. 6. На рисунке  <1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD.
<1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 13. На рисунке
АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 13. На рисунке  АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный.
АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный.