 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Образовательный минимум по алгебре за II четверть.
Математика Класс Глейх вадим Антонович– учитель математики, e-mail: spb_sport91@ mail.ru (отправляя письмо в графе «Кому», указываем «учителю математике Глейху В.А») Расписание консультаций:среда 15.00 – 16.00, пятница 15.00 – 16.00. Критерии оценивания учащихся спортсменов, выполнивших задание.Для получения положительной оценки по итогам четверти учащийся должен: 1) сдать зачёт-минимум по соответствующему предмету: Алгебра – до 18.12.2014, Геометрия – до 18.12.2014; 2) сдать учителю в отдельной тетради (12 листов) или прислать по электронной почте по указанному выше адресу в указанные сроки задания и пройти по ним собеседование; 3)написать в классе плановые контрольные работы: Алгебра: Контрольная работа № 3 до 27.11.2014 Контрольная работа № 4 до 20.12.2014 Геометрия: Контрольная работа № 2 до 17.12.2014. По итогам выполненного обьёма работ оценки «4 и 5» ставятся за правильно выполненные не менее 70% и 90% заданий соответственно, включая задания (*). Ооценка «3» ставится за правильно выполненные не менее 50% заданий, не включая задания (*).. Алгебра. | Задание 5а. Степень с натуральным показателем. Глава III. §9,10. Сдать до 20.11.2014 1. № 135(2,4,6), 136(2), 137(4), 139(2), 133(4), 134(3), 141(4), 142(4), 144(4), 145(4), 146(2,4), 147(4), 148(3), 150(4,5), 149*(2,4), 153*(3,4), 157*. 2. 160(4), 161(4), 162(4), 163(4,6), 164(6), 165(6), 166(6), 167(4), 168(4), 169(4), 170(4), 172(6), 173(4), 174(2), 176(4), 177(4), 178(4), 179(4), 180(4), 181(4), 184(8), 185(4), 186(4), 187(4), 188(4), 189(4), 190(4), 191(4), 192(4), 193(4), 194(4), 200*(3), 201*(2,4), 205(1,2). | Задание 7а. Многочлены.Глава III. §13,14. Сдать до 5.12.2014 №: 229 (2), 230 (4), 236 (2,4), 238 (2,4), 240 (2,4),241(2), 239 (2); Задача: Мастер изготавливает на 8 деталей в час больше, чем ученик. Ученик работал 6ч, а мастер 8ч и вместе они изготовили 232 детали. Сколько деталей в час изготовлял ученик? _ _ _ _ _ _ _ _ _ № (*) № 230 (2), 232, 234, 242(1), 243 (1); Задача: Автомобилист и грузовик выехали одновременно навстречу другу из пунктов А и В, расстояние между которыми 280 км. Средняя скорость автомобилиста на 20 км/ч больше средней скорости грузовика. Найдите скорость каждого автомобиля, если известно, что встретились они через 3ч и грузовик сделал в пути получасовую остановку. | Задание 9а. Действия с одночленами и многочленами. Глава III. §17,18. Сдать до 20.12.2014 №: 264 (2,4) – 266 (2,4), 269 (4), 275, 278 (2,4), 279 (2,4); Упростить и выяснить при каких значениях х, значение выражения № 272 (1) равно 0. _ _ _ _ _ _ _ _ _ _ _ № (*) 268 (2,4), 269 (2), 270 (2), 271(1), 273 (1), 277(1). Задача: Вы едете в автомобиле со скоростью 60 км/час. На сколько нужно увеличить скорость вашего автомобиля, чтобы проезжать 1 км пути на полминуты быстрее? | | Задание 6а. Одночлены. Глава III. §11,12. Сдать до 28.11.2014. №: 210 (2,4,6,8), 211(2), 213 (2,4) – 217 (2,4), 219(2), 221(2), 223 (2), 224(2,4). _ _ _ _ _ _ _ _ _ _ №* 218 (3), № 220 (2,4), 225 (2,4), Задача:   | | | Задание 10а. Способы разложения многочлена на множители. Глава IV. §19. Сдать до № 318 (2), 319 (2,4) – 333 (2,4), 337 (2,4). _ _ _ _ _ _ _ _ _ _ _ № (*) 333(4), 334(4), 335 (2,4), 336 (2,4), 337(6), 338. Задача: В Стране Чудес проводилось следствие по делу об украденной муке. На суде Мартовский Заяц заявил, что муку украл Болванщик. В свою очередь Болванщик и Соня дали показания, которые по каким-то причинам не были записаны. В ходе судебного процесса выяснилось, что муку украл лишь один из трех подсудимых и что только он дал правдивые показания. Кто украл муку? | | | Задание 8а. Действия с одночленами и многочленами. Глава III. §15,16. Сдать до 12.12.2014 №: 244 (2,4) – 246 (2,4), 248 (2), 249 (2), 250 (4), 261 (4), 256 (2,4) – 258 (2,4), 259(2), 260 (4), 255 (2), 261 (2); _ _ _ _ _ _ _ _ _ _ Задача: Пароход от Киева до Херсона плывет трое суток, а назад - четверо. Сколько суток будут плыть плоты от Киева до Херсона? | | | № (*) 249 (4), 251 (2), 252 (2), 261(1), 262 (2), 253, 263. | | Диагностическая контрольная работа № 3   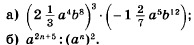  | Диагностическая контрольная работа № 4        | | | | | | | |
Геометрия.
Задание 5g. Перпендикулярные прямые. Глава I (§6. п.12). Сроки: 22.11.2014 1. На рисунке   . Найдите < ABF. 2. На рисунке . Найдите < ABF. 2. На рисунке    Докажите, что Докажите, что  . 3. Перерисуйте в тетрадь . . 3. Перерисуйте в тетрадь .  С помощью угольника и линейки найдите на прямой l точку, равноудаленную от концов отрезка АВ и СD. 4. Как, используя шаблон угла в 15°, построить перпендикулярные прямые. 5*. На прямой DE между точками D и Е выбрали точку F. Точка L не принадлежит прямой DE. Докажите, что если <DFL = <EFL, то DE перпендикулярен FL. 6*. Из вершины <АВС = 72°, проведены лучи BD и BF так, что С помощью угольника и линейки найдите на прямой l точку, равноудаленную от концов отрезка АВ и СD. 4. Как, используя шаблон угла в 15°, построить перпендикулярные прямые. 5*. На прямой DE между точками D и Е выбрали точку F. Точка L не принадлежит прямой DE. Докажите, что если <DFL = <EFL, то DE перпендикулярен FL. 6*. Из вершины <АВС = 72°, проведены лучи BD и BF так, что  , ,  , лучи BD и ВС принадлежат углу АВF. Найдите < DBF и < AFB. , лучи BD и ВС принадлежат углу АВF. Найдите < DBF и < AFB. | Задание 7g. Первый и второй признаки равенства треугольников. Глава II (§1. п.15, §3. п.19). Сроки: 5.12.2014 10. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3см и 4см, а угол между ними - 90°.Укажите вид этого треугольника. 11. С помощью линейки и транспортира постройте треугольник, Одна сторона которого равна 6см, а углы, прилежащие к этой стороне, - 90° и 45°. 12. На рисунке 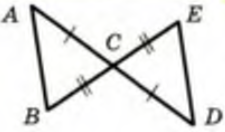 АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 13. На рисунке АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 13. На рисунке  АО = ОD, ВО = ОС. Найдите сторону СD и <ОСD треугольника ОСD, если АВ = 8см, <ОВА = 43°. 14. Дано: АО = ОD, ВО = ОС. Найдите сторону СD и <ОСD треугольника ОСD, если АВ = 8см, <ОВА = 43°. 14. Дано: 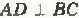 ВD = CD. ВD = CD.  Докажите, что АВ = АС. 15. На рисунке Докажите, что АВ = АС. 15. На рисунке 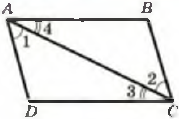 <1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. 16. На рисунке <1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. 16. На рисунке  <ВАО = <DСО, <ВАС = <DСА. Докажите, что ΔАВС = ΔАСD. 8. Через точку М, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках А и В. Докажите, что АМ = МВ. 17. На рисунке <ВАО = <DСО, <ВАС = <DСА. Докажите, что ΔАВС = ΔАСD. 8. Через точку М, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках А и В. Докажите, что АМ = МВ. 17. На рисунке  ΔМКО = ΔМРО. Докажите, что Δ КОЕ = ΔРОЕ. 18*. Отрезки АD и ВС пересекаются в точке О и делятся этой точкой пополам. Найдите <АСD, если <АВС = 64°, <АСО = 56°. 19*. Докажите, что в равных треугольниках медианы, проведённые к соответственным сторонам равны. 20*. Докажите равенство двух треугольников по стороне, медиане, проведённой к этой стороне и углу между этой стороной и медианой. ΔМКО = ΔМРО. Докажите, что Δ КОЕ = ΔРОЕ. 18*. Отрезки АD и ВС пересекаются в точке О и делятся этой точкой пополам. Найдите <АСD, если <АВС = 64°, <АСО = 56°. 19*. Докажите, что в равных треугольниках медианы, проведённые к соответственным сторонам равны. 20*. Докажите равенство двух треугольников по стороне, медиане, проведённой к этой стороне и углу между этой стороной и медианой. | | Задание 6g. Треугольник. Глава II (§1. п.14).Сроки: 27.11.2014 6. Трижды перерисуйте в тетрадь указанные.  треугольники. Проведите в каждом из них по 3 медианы, 3 высоты и 3 биссектрисы. 7. Периметр треугольника равен 48см, а его стороны относятся как 7 : 9 : 8. Найдите стороны треугольника. 3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. 8. Треугольники АВС и КТМ равны, угол А и угол М, В и К – соответственные, <С = 40°, МК = 5см. Найдите угол Т и сторону АВ. 9. Медиана ВD треугольника АВС, периметр которого равен 60см, разбивает его на два треугольника АВD DВС, периметры которых равны 36см и 50см. Чему равна длина медианы ВD? Задание 8g. Равнобедренный треугольник и его свойства. Глава II (§1. п.15, §3. п.19). Сроки: 11.12.2014 21. Периметр равнобедренного треугольника равен 28см, а боковая сторона 10 см.Найдите основание треугольника. 22. Найдите стороны равнобедренного треугольника, периметр которого равен 54 см, а основание в 4 раза меньше боковой стороны. 23. На рисунке треугольники. Проведите в каждом из них по 3 медианы, 3 высоты и 3 биссектрисы. 7. Периметр треугольника равен 48см, а его стороны относятся как 7 : 9 : 8. Найдите стороны треугольника. 3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. 8. Треугольники АВС и КТМ равны, угол А и угол М, В и К – соответственные, <С = 40°, МК = 5см. Найдите угол Т и сторону АВ. 9. Медиана ВD треугольника АВС, периметр которого равен 60см, разбивает его на два треугольника АВD DВС, периметры которых равны 36см и 50см. Чему равна длина медианы ВD? Задание 8g. Равнобедренный треугольник и его свойства. Глава II (§1. п.15, §3. п.19). Сроки: 11.12.2014 21. Периметр равнобедренного треугольника равен 28см, а боковая сторона 10 см.Найдите основание треугольника. 22. Найдите стороны равнобедренного треугольника, периметр которого равен 54 см, а основание в 4 раза меньше боковой стороны. 23. На рисунке  МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 24. Угол, смежный с углом при вершине равнобедренного треугольника, равен 76°. Найдите угол между боковой стороной треугольника и высотой, опущенной на основание. 25. Прямая пересекает стороны угла А в точках В и С МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 24. Угол, смежный с углом при вершине равнобедренного треугольника, равен 76°. Найдите угол между боковой стороной треугольника и высотой, опущенной на основание. 25. Прямая пересекает стороны угла А в точках В и С  так, что АВ = АС.Докажите, что <1=<2. 26. Используя признаки равенства треугольников, докажите признак равенства равнобедренных треугольников по основанию и прилежащему к нему углу. 27. В треугольнике МКЕ известно, что МК = МЕ. На стороне КЕ отмечены точки F и N так, что точка N лежит между точками F и E, причём <КМF = <ЕМN. Докажите, что <MFN = <MNF. 28. В равнобедренном треугольнике АВС с основанием АС на медиане ВD отметили произвольную точку М. Докажите. Что: 1) ΔАМВ = ΔСМВ; 2) ΔАМD = ΔСМD. 29*. Докажите. Что медианы равнобедренного треугольника, проведённые к боковым сторонам равны. 30*. Одна сторона равнобедренного треугольника равна 4см. Найдите две другие стороны, если периметр треугольника равен 14см. 31*На продолжении сторон АВ, ВС, АС равностороннего треугольника АВС (см. рис.) так, что АВ = АС.Докажите, что <1=<2. 26. Используя признаки равенства треугольников, докажите признак равенства равнобедренных треугольников по основанию и прилежащему к нему углу. 27. В треугольнике МКЕ известно, что МК = МЕ. На стороне КЕ отмечены точки F и N так, что точка N лежит между точками F и E, причём <КМF = <ЕМN. Докажите, что <MFN = <MNF. 28. В равнобедренном треугольнике АВС с основанием АС на медиане ВD отметили произвольную точку М. Докажите. Что: 1) ΔАМВ = ΔСМВ; 2) ΔАМD = ΔСМD. 29*. Докажите. Что медианы равнобедренного треугольника, проведённые к боковым сторонам равны. 30*. Одна сторона равнобедренного треугольника равна 4см. Найдите две другие стороны, если периметр треугольника равен 14см. 31*На продолжении сторон АВ, ВС, АС равностороннего треугольника АВС (см. рис.)  за точки А, В и С соответственно отложили равные отрезки АD, ВК и СЕ. Докажите, что ΔDЕК – равносторонний. за точки А, В и С соответственно отложили равные отрезки АD, ВК и СЕ. Докажите, что ΔDЕК – равносторонний. | | Задание 9g. Признаки равнобедренного треугольника. Глава II (§1. п.15, §3. п.19). Сроки: 17.12.2014 32. На рисунке  <АМК = <АСВ, АК = МК. Докажите, что ΔАВС – равнобедренный. 33. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 34. Точки М и К принадлежат соответственно боковым стонам АВ и ВС равнобедренного треугольника АВС, АМ = СК. Отрезки АК и СМ пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 35* На рисунке <АМК = <АСВ, АК = МК. Докажите, что ΔАВС – равнобедренный. 33. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 34. Точки М и К принадлежат соответственно боковым стонам АВ и ВС равнобедренного треугольника АВС, АМ = СК. Отрезки АК и СМ пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 35* На рисунке  <АВD = <АDВ, <СВD = <СDВ. Докажите, что ΔАВС = ΔАDС. 36*. На сторонах АВ и ВС треугольника АВС отметили соответственно точки Р и Е так, что < ЕАС = <РСА. Отрезки ЕА и СР пересекаются в точке М, РМ = ЕМ. Докажите, что ΔАВС – равнобедренный. 37*. Медиана АМ треугольника АВС перпендикулярна его биссектрисе ВК. Найдите сторону АВ, если В = 16см. <АВD = <АDВ, <СВD = <СDВ. Докажите, что ΔАВС = ΔАDС. 36*. На сторонах АВ и ВС треугольника АВС отметили соответственно точки Р и Е так, что < ЕАС = <РСА. Отрезки ЕА и СР пересекаются в точке М, РМ = ЕМ. Докажите, что ΔАВС – равнобедренный. 37*. Медиана АМ треугольника АВС перпендикулярна его биссектрисе ВК. Найдите сторону АВ, если В = 16см. | | Задание 10g. Третий признак равенства треугольников. Глава II (§1. п.15, §3. п.19). 20.12.2014 38. На рисунке  АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 39. На рисунке АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 39. На рисунке 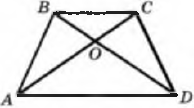 АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный. 40. На рисунке АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный. 40. На рисунке  АВ = СD, ВС = СD, ВМ – биссектриса угла АВС, DК – биссектриса угла АDС. Докажите, что ΔАВС = ΔВDС. 41* . Коля утверждает, что ему удалось сделать рисунок, АВ = СD, ВС = СD, ВМ – биссектриса угла АВС, DК – биссектриса угла АDС. Докажите, что ΔАВС = ΔВDС. 41* . Коля утверждает, что ему удалось сделать рисунок,  на котором АВ = АС и АМ = АN. Прав ли он? на котором АВ = АС и АМ = АN. Прав ли он? | | | Диагностическая контрольная работа № 2. | | | 1. На рисунке (справа) <СВМ = <АСF, РАВС = 34см, ВС = 12см. Найдите сторону АС треугольника АВС. 2. В Δ MNK < K = 37° <M = 69° NP – биссектриса Δ MNK. Докажите, что МР <РК. 3. Периметр равнобедренного треугольника равен 45см, а одна из его сторон больше другой на 12 см. Найдите стоны треугольника. |  | | | | | | |
Образовательный минимум по алгебре за II четверть. Теоретическая часть. Степень и её свойства. | Определение: а · а · … · а = аn, а1 = а, а0 = 1, где n € N, n > 1. n – раз | | an · am = an + m | | an· bn = (a·b)n | | an : am = an - m | |  = =  , b ≠ 0 , b ≠ 0 | | (an)m = an·m | Стандартный вид числа. Каждое число больше 10, можно записать в виде а·10n, где 10 ≥ а ≥ 1. Пр. 457 = 4,57·102. Одночлены и многочлены. Определение. Одночленом называется произведение числовых и буквенных множителей. Числовой множитель является коэффициентом одночлена. Любой одночлен можно записать встандартном виде, для этого: 1) перемножаются числовые множители и их произведение ставится на первое место; 2) перемножаются степени с одинаковыми основаниями. Их произведения ставится после числового коэффициента. Пр. 6ав2с  а3 = 10а4в2с. а3 = 10а4в2с. Определение. Многочленом называется алгебраическая сумма нескольких одночленов.
|








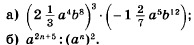









 . Найдите < ABF. 2. На рисунке
. Найдите < ABF. 2. На рисунке 

 Докажите, что
Докажите, что  . 3. Перерисуйте в тетрадь .
. 3. Перерисуйте в тетрадь .  С помощью угольника и линейки найдите на прямой l точку, равноудаленную от концов отрезка АВ и СD. 4. Как, используя шаблон угла в 15°, построить перпендикулярные прямые. 5*. На прямой DE между точками D и Е выбрали точку F. Точка L не принадлежит прямой DE. Докажите, что если <DFL = <EFL, то DE перпендикулярен FL. 6*. Из вершины <АВС = 72°, проведены лучи BD и BF так, что
С помощью угольника и линейки найдите на прямой l точку, равноудаленную от концов отрезка АВ и СD. 4. Как, используя шаблон угла в 15°, построить перпендикулярные прямые. 5*. На прямой DE между точками D и Е выбрали точку F. Точка L не принадлежит прямой DE. Докажите, что если <DFL = <EFL, то DE перпендикулярен FL. 6*. Из вершины <АВС = 72°, проведены лучи BD и BF так, что  ,
,  , лучи BD и ВС принадлежат углу АВF. Найдите < DBF и < AFB.
, лучи BD и ВС принадлежат углу АВF. Найдите < DBF и < AFB.  АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 13. На рисунке
АВ = СD, <ВАС = <САD. Докажите, что ΔАВС = ΔАDС. 13. На рисунке  АО = ОD, ВО = ОС. Найдите сторону СD и <ОСD треугольника ОСD, если АВ = 8см, <ОВА = 43°. 14. Дано:
АО = ОD, ВО = ОС. Найдите сторону СD и <ОСD треугольника ОСD, если АВ = 8см, <ОВА = 43°. 14. Дано: 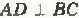 ВD = CD.
ВD = CD.  Докажите, что АВ = АС. 15. На рисунке
Докажите, что АВ = АС. 15. На рисунке  <1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. 16. На рисунке
<1 = <2,<3 = <4, АВ = 8см. ВС = 6см. Найдите стороны АD и СD треугольника АСD. 16. На рисунке  <ВАО = <DСО, <ВАС = <DСА. Докажите, что ΔАВС = ΔАСD. 8. Через точку М, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках А и В. Докажите, что АМ = МВ. 17. На рисунке
<ВАО = <DСО, <ВАС = <DСА. Докажите, что ΔАВС = ΔАСD. 8. Через точку М, принадлежащую биссектрисе угла с вершиной в точке О, провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках А и В. Докажите, что АМ = МВ. 17. На рисунке  ΔМКО = ΔМРО. Докажите, что Δ КОЕ = ΔРОЕ. 18*. Отрезки АD и ВС пересекаются в точке О и делятся этой точкой пополам. Найдите <АСD, если <АВС = 64°, <АСО = 56°. 19*. Докажите, что в равных треугольниках медианы, проведённые к соответственным сторонам равны. 20*. Докажите равенство двух треугольников по стороне, медиане, проведённой к этой стороне и углу между этой стороной и медианой.
ΔМКО = ΔМРО. Докажите, что Δ КОЕ = ΔРОЕ. 18*. Отрезки АD и ВС пересекаются в точке О и делятся этой точкой пополам. Найдите <АСD, если <АВС = 64°, <АСО = 56°. 19*. Докажите, что в равных треугольниках медианы, проведённые к соответственным сторонам равны. 20*. Докажите равенство двух треугольников по стороне, медиане, проведённой к этой стороне и углу между этой стороной и медианой.  треугольники. Проведите в каждом из них по 3 медианы, 3 высоты и 3 биссектрисы. 7. Периметр треугольника равен 48см, а его стороны относятся как 7 : 9 : 8. Найдите стороны треугольника. 3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. 8. Треугольники АВС и КТМ равны, угол А и угол М, В и К – соответственные, <С = 40°, МК = 5см. Найдите угол Т и сторону АВ. 9. Медиана ВD треугольника АВС, периметр которого равен 60см, разбивает его на два треугольника АВD DВС, периметры которых равны 36см и 50см. Чему равна длина медианы ВD? Задание 8g. Равнобедренный треугольник и его свойства. Глава II (§1. п.15, §3. п.19). Сроки: 11.12.2014 21. Периметр равнобедренного треугольника равен 28см, а боковая сторона 10 см.Найдите основание треугольника. 22. Найдите стороны равнобедренного треугольника, периметр которого равен 54 см, а основание в 4 раза меньше боковой стороны. 23. На рисунке
треугольники. Проведите в каждом из них по 3 медианы, 3 высоты и 3 биссектрисы. 7. Периметр треугольника равен 48см, а его стороны относятся как 7 : 9 : 8. Найдите стороны треугольника. 3.Одна сторона треугольника равна 24см, вторая на 18см больше первой, а третья сторона в 2 раза меньше второй. Найдите периметр треугольника. 8. Треугольники АВС и КТМ равны, угол А и угол М, В и К – соответственные, <С = 40°, МК = 5см. Найдите угол Т и сторону АВ. 9. Медиана ВD треугольника АВС, периметр которого равен 60см, разбивает его на два треугольника АВD DВС, периметры которых равны 36см и 50см. Чему равна длина медианы ВD? Задание 8g. Равнобедренный треугольник и его свойства. Глава II (§1. п.15, §3. п.19). Сроки: 11.12.2014 21. Периметр равнобедренного треугольника равен 28см, а боковая сторона 10 см.Найдите основание треугольника. 22. Найдите стороны равнобедренного треугольника, периметр которого равен 54 см, а основание в 4 раза меньше боковой стороны. 23. На рисунке  МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 24. Угол, смежный с углом при вершине равнобедренного треугольника, равен 76°. Найдите угол между боковой стороной треугольника и высотой, опущенной на основание. 25. Прямая пересекает стороны угла А в точках В и С
МК = КЕ, ОЕ = 6см, <МКЕ = 48°, <РОЕ = 90°. Найдите сторону МЕ и <МКО. 24. Угол, смежный с углом при вершине равнобедренного треугольника, равен 76°. Найдите угол между боковой стороной треугольника и высотой, опущенной на основание. 25. Прямая пересекает стороны угла А в точках В и С  так, что АВ = АС.Докажите, что <1=<2. 26. Используя признаки равенства треугольников, докажите признак равенства равнобедренных треугольников по основанию и прилежащему к нему углу. 27. В треугольнике МКЕ известно, что МК = МЕ. На стороне КЕ отмечены точки F и N так, что точка N лежит между точками F и E, причём <КМF = <ЕМN. Докажите, что <MFN = <MNF. 28. В равнобедренном треугольнике АВС с основанием АС на медиане ВD отметили произвольную точку М. Докажите. Что: 1) ΔАМВ = ΔСМВ; 2) ΔАМD = ΔСМD. 29*. Докажите. Что медианы равнобедренного треугольника, проведённые к боковым сторонам равны. 30*. Одна сторона равнобедренного треугольника равна 4см. Найдите две другие стороны, если периметр треугольника равен 14см. 31*На продолжении сторон АВ, ВС, АС равностороннего треугольника АВС (см. рис.)
так, что АВ = АС.Докажите, что <1=<2. 26. Используя признаки равенства треугольников, докажите признак равенства равнобедренных треугольников по основанию и прилежащему к нему углу. 27. В треугольнике МКЕ известно, что МК = МЕ. На стороне КЕ отмечены точки F и N так, что точка N лежит между точками F и E, причём <КМF = <ЕМN. Докажите, что <MFN = <MNF. 28. В равнобедренном треугольнике АВС с основанием АС на медиане ВD отметили произвольную точку М. Докажите. Что: 1) ΔАМВ = ΔСМВ; 2) ΔАМD = ΔСМD. 29*. Докажите. Что медианы равнобедренного треугольника, проведённые к боковым сторонам равны. 30*. Одна сторона равнобедренного треугольника равна 4см. Найдите две другие стороны, если периметр треугольника равен 14см. 31*На продолжении сторон АВ, ВС, АС равностороннего треугольника АВС (см. рис.)  за точки А, В и С соответственно отложили равные отрезки АD, ВК и СЕ. Докажите, что ΔDЕК – равносторонний.
за точки А, В и С соответственно отложили равные отрезки АD, ВК и СЕ. Докажите, что ΔDЕК – равносторонний. <АМК = <АСВ, АК = МК. Докажите, что ΔАВС – равнобедренный. 33. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 34. Точки М и К принадлежат соответственно боковым стонам АВ и ВС равнобедренного треугольника АВС, АМ = СК. Отрезки АК и СМ пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 35* На рисунке
<АМК = <АСВ, АК = МК. Докажите, что ΔАВС – равнобедренный. 33. Биссектрисы АМ и СК углов при основании АС равнобедренного треугольника АВС пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 34. Точки М и К принадлежат соответственно боковым стонам АВ и ВС равнобедренного треугольника АВС, АМ = СК. Отрезки АК и СМ пересекаются в точке О. Докажите, что ΔАОС – равнобедренный. 35* На рисунке  <АВD = <АDВ, <СВD = <СDВ. Докажите, что ΔАВС = ΔАDС. 36*. На сторонах АВ и ВС треугольника АВС отметили соответственно точки Р и Е так, что < ЕАС = <РСА. Отрезки ЕА и СР пересекаются в точке М, РМ = ЕМ. Докажите, что ΔАВС – равнобедренный. 37*. Медиана АМ треугольника АВС перпендикулярна его биссектрисе ВК. Найдите сторону АВ, если В = 16см.
<АВD = <АDВ, <СВD = <СDВ. Докажите, что ΔАВС = ΔАDС. 36*. На сторонах АВ и ВС треугольника АВС отметили соответственно точки Р и Е так, что < ЕАС = <РСА. Отрезки ЕА и СР пересекаются в точке М, РМ = ЕМ. Докажите, что ΔАВС – равнобедренный. 37*. Медиана АМ треугольника АВС перпендикулярна его биссектрисе ВК. Найдите сторону АВ, если В = 16см. АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 39. На рисунке
АС = АD, ВС = ВD. Найдите угол ВАС, если <ВАD = 25°. 39. На рисунке  АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный. 40. На рисунке
АВ = СD, АС = ВD. Докажите, что ΔВОС – равнобедренный. 40. На рисунке  АВ = СD, ВС = СD, ВМ – биссектриса угла АВС, DК – биссектриса угла АDС. Докажите, что ΔАВС = ΔВDС. 41* . Коля утверждает, что ему удалось сделать рисунок,
АВ = СD, ВС = СD, ВМ – биссектриса угла АВС, DК – биссектриса угла АDС. Докажите, что ΔАВС = ΔВDС. 41* . Коля утверждает, что ему удалось сделать рисунок,  на котором АВ = АС и АМ = АN. Прав ли он?
на котором АВ = АС и АМ = АN. Прав ли он?
 =
=  , b ≠ 0
, b ≠ 0 а3 = 10а4в2с.
а3 = 10а4в2с.