 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Ортотреугольник отсекает треугольники, подобные данному 12
Теорема о высоте прямоугольного треугольника Если высота в прямоугольном треугольнике ABC длиной · · ·
Свойства оснований высот треугольника · Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами. · Описанная около ортотреугольника окружность - окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника. Другая формулировка последнего свойства: · Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек). · Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному. · Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность. Другие свойства высот треугольника · Если треугольник разносторонний (неравносторонний), то его внутренняя биссектриса, проведённая из любой вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины. · Высота треугольника изогонально сопряжена диаметру (радиусу) описанной окружности, проведенному из той же самой вершины. · В остроугольном треугольнике две его высоты отсекают от него подобные треугольники. · В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Свойства минимальной из высот треугольника Минимальная из высот треугольника обладает многими экстремальными свойствами. Например: · Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот. · Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины. · При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника. · Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
Основные соотношения · · · · · где
где
· Высота равнобедренного треугольника, опущенная на основание:
где
· Медианы и высоты в равностороннем треугольнике Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника. А в равносторонних треугольниках медианы и высоты - одно и то же. 1)
Рассмотрим произвольный треугольник ABC. Обозначим буквой O точку пересечения его медиан AA1 и BB1 и проведем среднюю линию A1B1 этого треугольника Медианы треугольника пересекаются в одной точке Отрезок A1B1 параллелен стороне AB, поэтому углы 1 и 2, а также углы 3 и 4 равны как накрест лежащие углы при пересечении параллельных прямых AB и A1B1 секущими AA1 и BB1. Следовательно, треугольники AOB и A1OB1 подобны по двум углам, и, значит их стороны пропорциональны: AOA1O=BOB1O=ABA1B1 . Но AB=2⋅A1B1, поэтому AO=2⋅A1O и BO=2⋅B1O. Таким образом, точка O пересечения медиан AA1 и BB1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка пересечения медиан BB1 и CC1 делит каждую из них в отношении 2:1 считая от вершины, и, следовательно, совпадает с точкой O. Итак, все три медианы треугольника ABC пересекаются в точке O и делятся ею в отношении 2:1, считая от вершины. Теорема доказана.
2)
Представим что в вершинах угла m₁=1, тогда в точках A₁,B₁,C₁, m₂=2, так как они являются серединами сторон. И тут можно заметить, что отрезки AA₁,BB₁,CC₁, которые пересекаются в одной точке и похожи на рычаги с точкой опоры О, где AO-l₁, a OA₁-l₂(плечи). И по физической формуле F₁/F₂=l₁/l₂, где F=m*g, где g-const, и она соответственно сокращается, получается m₁/m₂=l₁/l₂ т.е. ½=1/2. Теорема доказана.
Ортотреугольник Свойства: · Три высоты треугольника пересекаются в одной точке, эта точка носит название ортоцентра · Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника · Высоты треугольника являются биссектрисами ортотреугольника · Ортотреугольник-это треугольник с наименьшим периметром, который можно вписать в данный треугольник (задача Фаньяно) · Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла из которого он исходит. · Если точки A1, B1 и C1 на сторонах соответственно BC, AC и AB остроугольного треугольника ABC таковы, что
то
Ортотреугольник отсекает треугольники, подобные данному
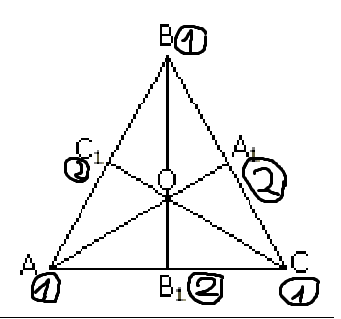
Теорема о свойстве биссектрис ортотреугольника
CC₁-биссектриса ∟B₁C₁A AA₁-биссектриса ∟B₁A₁C₁ BB₁-биссектриса ∟A₁B₁C₁
12 |
, проведённая из вершины прямого угла, делит гипотенузу длиной 
на отрезки 
и 
, соответствующие катетам 
и 
, то верны следующие равенства:
; 
где 
— площадь треугольника, 
— длина стороны треугольника, на которую опущена высота.
где 
- произведение боковых сторон, 
радиус описанной окружности
,
— радиус вписанной окружности.
где 
.
— высота в равностороннем треугольнике.
, 
и 
,
— ортотреугольник треугольника ABC.
∟B₁C₁C=∟B₁BC=∟CAA₁=∟CC₁A