 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Коэффициент Фехнера (коэффициент корреляции знаков)
Следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Он основан на сравнении поведения отклонений индивидуальных значений каждого признака ( Коэффициент Фехнера (
Очевидно, что если знаки всех отклонений по каждому признаку совпадают, то
Пример 9.3. Имеются следующие данные о росте восьми пар братьев и сестер (таблица 9.2). Таблица 9.2 - Данные о росте восьми пар братьев и сестер
Определить тесноту зависимости между ростом братьев и сестер на основе: а) коэффициента Фехнера; б) коэффициентов корреляции рангов Спирмэна и Кендэла. Решение: а) Рассчитаем средние величины
Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (
Коэффициент Фехнера (
По величине коэффициента Фехнера ( б) По уже имеющимся данным (графы 1-2 таблицы 9.2) для нахождения коэффициентов корреляции рангов Спирмэна и Кендэла построим таблицу 9.3.
Таблица 9.3 – Расчетные значения, необходимые для исчисления коэффициентов корреляции рангов Спирмэна и Кендэла
В данном примере отдельные значения Расчет рангов показан в графах 3 и 4. Для случая повторяющихся ранговесть особые скорректированные формулы и для коэффициента Спирмэна, и для коэффициента Кендэла. Однако на практике часто пользуются приведенной ранее формулой Спирмэна и для случая повторяющихся рангов, поскольку ошибку она дает весьма малую:
Формула коэффициента Кендэла для повторяющихся ранговимеет вид:
где
Так как значения рангов
Расчет Отсюда коэффициент корреляции рангов Кендэла:
По величине коэффициента ( Говоря о расчете коэффициента Кендэла, следует еще раз подчеркнуть, что если наблюдаемые единицы совокупности записаны неупорядоченно по одному из признаков (таблица 9.2.), то после ранжирования значений Коэффициент конкордации Корреляция рангов (
где
а) б) Коэффициент конкордации часто используется в экспертных оценках для определения согласованности мнений Пример 9.4.Пусть имеются следующие данные по пяти фирмам (графы 1-4 таблицы 9.4). Таблица 9.4 – Исходные данные и промежуточные расчеты коэффициентов конкордации
Определить тесноту зависимости между Решение: 1. Ранжираем каждый и трех показателей (графы 5-7). 2. Находим сумму рангов по каждой строке (графа 8) и общую сумму пяти строк 3. Возводим в квадрат сумму рангов в каждой строке и находим сумму пяти строк (графа 9):
4. Находим
5. Рассчитаем коэффициент конкордации:
Учитывая малое значение коэффициента конкордации, можно сказать, что зависимость между рассматриваемыми показателями весьма незначительна. Существуют и другие коэффициенты для измерения тесноты зависимости (коэффициенты ассоциации Непараметрические методы Применение корреляционного и регрессионного анализа требует, чтобы все признаки были количественно измеренными. Построение аналитических группировок предполагает, что количественным должен быть результативный признак. Параметрические методы основаны на использовании основных количественных параметров распределения (средних величин и дисперсий). Вместе с тем в статистике применяются также непараметрические методы, с помощью которых устанавливается связь между качественными (атрибутивными) признаками. Сфера их применения шире, чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты. В практике статистических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации. Для расчета коэффициента ассоциации строится четырехклеточная корреляционная таблица, которая носит название таблицы «четырех полей» и имеет следующий вид:
Применительно к таблице «четырех полей» с частотами
Коэффициент ассоциации изменяется от -1 до +1; чем ближе к +1 или -1, тем сильнее связаны между собой изучаемые признаки. Если
Пример 9.5. Имеющиеся данные о росте отцов и сыновей представлены в таблице 9.5. Таблица 9.5 - Распределение отцов и сыновей по росту, чел.
Подсчитаем коэффициент ассоциации по данным таблицы 9.5:
Поскольку Если по каждому из взаимосвязанных признаков выделяется число групп более двух, то для подобного рода таблиц теснота связи между качественными признаками может быть измерена с помощью показателя взаимной сопряженности А.A. Чупрова:
где
Вычтя из этой суммы единицу, получим Коэффициент взаимной сопряженности А.А. Чупрова изменяется от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков. Пример 9.6. Данные об уровне образования членов 100 семей приведены в таблице 9.6. Таблица 9.6-Распределение семей по уровню образования мужа и жены
Примечание: частоты - верхние строки; их квадраты (в скобках) - средние строки; квадраты частот, деленные на суммы частот по столбцу - нижние строки; в итоговых столбцах - сумма частот, сумма результатов деления (А), а также результат деления нижнего числа на верхнее - последний столбец (В).
Тогда Коэффициент взаимной сопряженности А.А. Чупрова:
Его значение показывает заметную связь между уровнями образования мужа и жены при формировании семьи.
|
и 
) от своей средней величины. При этом во внимание принимаются не величины отклонений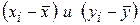 
, а их знаки («+» или «-»). Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений ( 
) и несовпадений ( 
).
)рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:
. (9.12)
и тогда 
. Это характеризует наличие прямой связи. Если все знаки не совпадают, то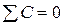 
, а 
, что характеризует обратную связь. Коэффициент Фехнера, как и любой другой показатель тесноты связи, может принимать значения от -1 до +1.
;
.
) и несовпадений ( 
):
.
)рассчитывается по формуле 9.8:
.
) можно сделать вывод о весьма тесной зависимости между 
.
,
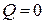
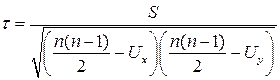, как и раньше, a 
и 
-показатели, корректирующие максимальную сумму баллов и определяемые по формуле 
, где 
- число повторяющихся рангов в соответствующем ряду 
.
в шести случаях идут значения 
и ни одного случая, где 
. Это означает, что в графу 7 мы ставим число «6», а в графу 8число «0». Далее после второй пары значений рангов, где 
в четырех случаях идут значения 
и ни одного случая, где 
. Это означает, что в графу 7 мы ставим число «4», а в графу 8число «0». ». В случае, если бы после второй пары значений рангов, где 
и 
показан в графах 7 и 8. По результатам подсчетов 
.
.
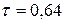) можно сделать вывод о весьма тесной зависимости между 
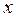и 
, т.е. рост сестры весьма зависим от роста её брата.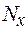
, следует переписать, расположив их строго в порядке возрастания (или убывания), а для второго признака сохранить значения рангов, соответствующие значениям каждого 
)может определяться не только для двух, но и для большего числа показателей (факторов). Исчисляемый в этом случае показатель именуется коэффициентом конкордации( 
)и рассчитывается по формуле:
, (9.13)
- количество коррелируемых факторов;
- число наблюдений;
- сумма квадратов отклонений суммы рангов по 
или, что по значению тоже самое, (9.14)
где 
- ранг 
-го показателя. (9.15)
исследуемыми факторами или объектами по их приоритетности.
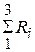
с помощью коэффициента конкордации.
.
, используя формулу 9.11:
.
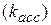и контингенции 
; коэффициент взаимной сопряженности Пирсона 
; коэффициент Чупрова 
), которые применяются достаточно редко.
и 
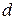коэффициент ассоциации выражается формулой:
. (9.16)
не менее 0,3, то это свидетельствует о наличии связи между качественными признаками.
, между ростом отцов и сыновей существует корреляционная связь.
(9.17)
- число возможных значений первой статистической величины (число групп по столбцам);
- число возможных значений второй статистической величины (число групп по строкам);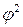
- показатель взаимной сопряженности (определяется как сумма отношений квадратов частот клетки таблицы распределения к произведению итоговых частот соответствующего столбца и строки).
, 
.
.