 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ)
Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной корреляционной связи ( уравнение регрессии)имеет вид:
где
Поскольку Коэффициент парной линейной регрессии Параметры уравнения
Для нахождения минимума функции приравниваем к нулю её частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
Решим эту систему в общем виде, находим параметры уравнения
Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:
Определив значения Пример 9.1.Рассмотрим построение однофакторного уравнения регрессии зависимости объема предоставленных кредитов Исходя из экономических соображений предоставленные кредиты выбраны в качестве независимой переменной Таблица 9.1 - Распределение лет по сумме предоставленных кредитов и задолженности по ним, в рублях
Пользуясь расчетными значениями (см. таблицу 9.1), исчислим параметры для данного уравнения регрессии:
Следовательно, регрессионная модель распределения задолженности по предоставленным кредитам в рублях дляданного примера может быть записана в виде конкретного простого уравнения регрессии:
Это уравнение характеризует зависимость среднего уровня предоставленных в рублях кредитов от задолженности по ним. Расчетные значения Корреляционный анализ имеет своей задачей количественное определение тесноты связи не только между двумя признаками (при парной связи), но и между результативным признаком и множеством факторных признаков (при многофакторной связи).
|



 , на результативный признак
, на результативный признак  и представляющая собой однофакторный корреляционный и регрессионный анализ.
и представляющая собой однофакторный корреляционный и регрессионный анализ. , (9.3)
, (9.3) - теоретические значения результативного признака, полученные по уравнению регрессии;
- теоретические значения результативного признака, полученные по уравнению регрессии; - коэффициенты (параметры) уравнения регрессии.
- коэффициенты (параметры) уравнения регрессии. является средним значением
является средним значением  , экономическая интерпретация часто затруднена или вообще невозможна.
, экономическая интерпретация часто затруднена или вообще невозможна. имеет смысл показателя силы связимежду вариацией факторного признака
имеет смысл показателя силы связимежду вариацией факторного признака  находят методом наименьших квадратов- метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений. Таким образом, в основу данного метода положено требование минимальности сумм квадратов отклонений эмпирических данных
находят методом наименьших квадратов- метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений. Таким образом, в основу данного метода положено требование минимальности сумм квадратов отклонений эмпирических данных  от выровненных
от выровненных 
 (9.4)
(9.4) (9.5)
(9.5) (9.6)
(9.6) или
или  ,
, .
. , подставив их в уравнение связи
, подставив их в уравнение связи  , находим значения
, находим значения 
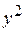



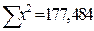



 ,
, .
. .
.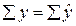 (
(  ,
, (возникло некоторое расхождение вследствие округления расчетов)).
(возникло некоторое расхождение вследствие округления расчетов)).