ПОЗНАВАТЕЛЬНОЕ

Сила воли ведет к действию, а позитивные действия формируют позитивное отношение

Как определить диапазон голоса - ваш вокал

Игровые автоматы с быстрым выводом

Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими

Целительная привычка

Как самому избавиться от обидчивости

Противоречивые взгляды на качества, присущие мужчинам

Тренинг уверенности в себе

Вкуснейший "Салат из свеклы с чесноком"

Натюрморт и его изобразительные возможности

Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.

Как научиться брать на себя ответственность

Зачем нужны границы в отношениях с детьми?

Световозвращающие элементы на детской одежде

Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия

Как слышать голос Бога

Классификация ожирения по ИМТ (ВОЗ)

Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Допуски угловых размеров и конусов

В международной системе единиц СИ в качестве основной единицы плоского угла установлен радиан – угол между двумя радиусами окружности, длина дуги между которыми равна радиусу. Такая единица измерения углов, удобная для расчетов, практически не применяется на практике ввиду отсутствия приборов, проградуированных в радианах. Поэтому в машиностроении в качестве единицы измерения используют градусы (1/360 окружности), минуты (1/60 градуса) и секунды (1/60 минуты) (1 рад. = 360/2p = 57°17¢44,8²).

Для призматических деталей кроме углов допускается применение уклонов, например: уклон 1:500 соответствует углу уклона b = 6¢52,5²или 0,002 радиана. Для конусов, наряду с углами используется понятие конусность:

С = (D – d)/L = 2tg(a/2),

где D – d - разность диаметров двух поперечных сечений конуса;

L - расстояние между двумя сечениями.

Конусность часто выражают в виде отношения, например, С = 1:20, где 20 - расстояние между поперечными сечениями конуса, разность диаметров которых равна 1 мм.

Нормальные углы, обычно применяемые в машиностроении, регламентируются ГОСТ 8908-81. Приведенные в этом документе значения нормальных углов не распространяются на углы, связанные расчетными зависимостями с другими размерами, и на углы конусов.

Нормальные конусности и углы конусов приведены в ГОСТ 8596-81. Стандартом предусмотрены два ряда конусности и углов конусов с предпочтительным применением первого ряда перед вторым. Наряду с этим для специального применения предусмотрена конусность для инструментальных конусов (конуса Морзе с номерами от 1 до 6).

Допуски углов конусов и призматических элементов деталей с длиной меньшей стороны до 2500 мм установлены ГОСТ 8908-81. Стандартом установлены 17 степеней точности углов, самая точная 1 степень, самая грубая 17. Допуск угла, выраженный разностью между наибольшим и наименьшим предельными углами, обозначается АТ, а допуск угла заданной точности дополняется номером соответствующей степени точности, например: АТ8, АТ9 и т.д.

Величины допусков на углы определены в зависимости от наименьшей стороны угла, так как точность изготовления и измерения угловых размеров зависит от длины стороны, и чем она меньше, тем точность ниже. Степени точности с 1 по 7 обычно применяются при изготовлении угловых мер и калибров.

В стандарте установлены следующие виды допусков:

АТ_a – допуск угла в угловых единицах (радианах или микрорадианах);

АТ¢_a – округленное значение допуска угла в градусах, минутах и секундах;

АТ_h – допуск угла, выраженный отрезком на перпендикуляре к стороне угла, противолежащем углу АТ_a на расстоянии L₁ от вершины этого угла в мкм (рисунок 45,а);

АТ_D – допуск угла конуса, выраженный допуском на разность диаметров в двух нормальных к оси сечениях конуса на заданном расстоянии L между ними (рисунок 45,б).

Пример задания величины допуска для восьмой степени точности приведен в таблице 18.

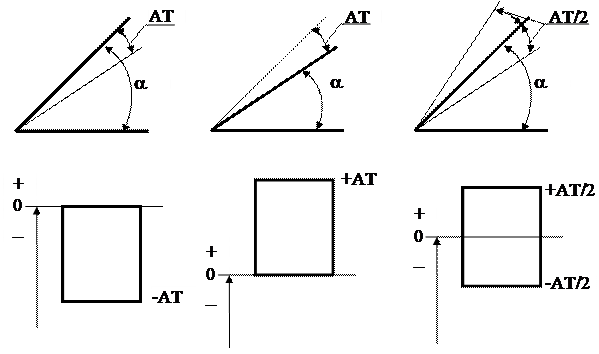
Рисунок 45 - Отклонения углов и конусов

Таблица 18 - Допуски углов

AТ_h = AT_a×L₁×10³, где AТ_h – в мкм, AT_a – в мкрад, L₁ – длина меньшей стороны угла в мм.

Значение АТ_D/2 относится только к конусам с конусностью не более 1:3, для которых AT_D = AТ_h. Для конусов с конусностью более 1:3 AT_D определяется по формуле

AT_D = AТ_h/cos(a/2),

где a – угол конуса.

Поле допуска угла может быть расположено относительно номи-нального угла односторонне или симметрично. Возможные расположения допуска и соответствующие им поля допусков приведены на рисунке 46.

Рисунок 46 - Расположение полей допусков углов

Аналогичное расположение полей допусков относительно номинального угла принято и для конусов.

Отдельную группу составляют инструментальные конуса, которые широко применяются для конических хвостовиков режущего инструмента, конических отверстий шпинделей станков и различных станочных приспособлений. К инструментальным конусам относятся конусы метрические и конусы Морзе, перечень и основные размеры которых приведены в ГОСТ 25577-82.

Метрические конусы имеют постоянную конусность С = 1 : 20 и нормируются по размеру наибольшего диаметра конического соединения в миллиметрах. Существуют инструментальные конусы с диаметрами соответственно: 4, 6, 80, 100, 120, 180 и 200.

Конусность в конусах Морзе является переменной и угол конуса колеблется около 3°. Обозначают конусы Морзе условными номерами 0, 1, 2, 3, 4, 5, 6. Кроме того, ГОСТ 9953-82 устанавливает размеры и обозначения укороченных конусов Морзе. Они обозначаются В7, В10, В12, В16, В18, В22, В24, В32, В45, где цифра соответствует примерному наибольшему диаметру конуса.

В ГОСТ 25577-82 и ГОСТ 9953-82 указаны размеры всех элементов метрических конусов и конусов Морзе, что позволяет в технической документации и на чертежах ограничиваться только их условным обозначением.

Допуски, методы и средства контроля инструментальных конусов регламентирует ГОСТ 2848-75. Для всех видов указанных конусов установлено пять степеней точности: АТ4, АТ5, АТ6, АТ7 и АТ8. В каждой степени отдельно нормируются предельные отклонения конусности на базовой длине в мкм, отклонение от прямолинейности образующей и отклонения от круглости в любом сечении по длине конуса.

Отклонение угла конуса от номинального размера следует располагать «в плюс» для наружных конусов и в «минус» для внутренних. Степени точности АТ4 и АТ5 можно применять только для наружных конусов. Примеры размеров и отклонений инструментальных конусов приведены в таблице 19.

Размеры, допуски и посадки конусов установлены ГОСТ 2.320-82. Например, условное обозначение метрического конуса седьмой степени точности с примерным наибольшим диаметром 120 мм:

Метр. 120 АТ7 ГОСТ 25577-82.

Таблица 19 - Предельные отклонения инструментальных конусов

Условное обозначение конуса Морзе №3 восьмой степени точности:

Морзе 3 АТ8 ГОСТ 25577-82.

Условное обозначение укороченного конуса Морзе с примерным диаметром 22 мм и седьмой степенью точности:

Морзе В22 АТ7 ГОСТ9953-82.

Приложение А