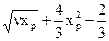ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Универсальные тесты для анализа случайных последовательностей.
Критерий c2. Критерий c2 ("хи-квадрат"), вероятно, самый распространенный из всех статистических критериев. Он используется не только сам по себе, но и как составная часть многих других тестов. Прежде чем приступить к общему описанию критерия c2, рассмотрим сначала в качестве примера, как можно было бы применить этот критерий для анализа игры в кости. Пусть каждый раз бросаются независимо две "правильные" кости, причем бросание каждой из них приводит с равной вероятностью к выпадению одного из чисел 1, 2, 3, 4, 5 и 6. Вероятности выпадения любой суммы s при одном бросании представлены в таблице: Сумма s= 2 3 4 5 6 7 8 9 10 11 12 Вероятность ps==1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36 (1) (Например, сумма s==4 может быть получена тремя способами: 1+3, 2+2, 3 +1; при 36 возможных исходах это составляет 3/36=1/12=p4.) Если бросать кости п раз, можно ожидать, что сумма s появится в среднем прs раз. Например, при 144 бросаниях значение 4 должно появиться около 12 раз. Следующая таблица показывает, какие результаты были в действительности получены при 144 бросаниях. Сумма s= 2 3 4 5 6 7 8 9 10 11 12 Фактическое число Ys= 2 4 10 12 22 29 21 15 14 9 6 выпадений (2) Среднее число выпа- прs = 4 8 12 16 20 24 20 16 12 8 4 дений Отметим, что фактическое число выпадений отличается от среднего во всех случаях. В этом нет ничего удивительного. Дело в том, что всего имеется 36144 возможных последовательностей исходов для 144 бросаний, и все они равновероятны. Одна из таких последовательностей состоит, например, только из двоек ("змеиные глаза"), и каждый, у кого "змеиные глаза" выпадут подряд 144 раза, будет уверен, что кости поддельные. Между тем эта последовательность так же вероятна, как и любая другая. Каким же образом в таком случае мы можем проверить, правильно ли изготовлена данная пара костей? Ответ заключается в том, что сказать определенно "да" или "нет" мы не можем, но можем дать вероятностный ответ, т. е. указать, насколько вероятно или невероятно данное событие. Естественный путь решения нашей задачи состоит в следующем. Вычислим (прибегнув к помощи ЭВМ) сумму квадратов разностей фактического числа выпадений Ys и среднего числа выпадений прs, (см. (2)): V=(Y2,-np2)2+(Y3-np3)2+ ... +(Y12-np12)2. (3) Для плохого комплекта костей должны получаться относительно высокие значения V. Возникает вопрос, насколько вероятны такие высокие значения? Если вероятность их появления очень мала, скажем, равна 1/100,—т.е. отклонение результата от среднего значения на такую большую величину возможно только в одном случае из 100,—то у нас есть определенные основания для подозрений. (Не следует забывать, однако, что даже хорошие кости будут давать такое высокое значение V один раз из 100, так что для большей уверенности следовало бы повторить эксперимент и посмотреть, получится ли повторно высокое значение V.) В статистику V все квадраты разностей входят с равным весом, хотя (Y7—пр7)2, например, вероятно, будет намного больше, чем (Y2—np2)2, так как s=7 встречается в шесть раз чаще, чем s=2. Оказывается, что в "правильную" статистику, или по крайней мере такую, для которой доказано, что она наиболее значима, член (Y7—пр7)2 входит с множителем, который в шесть раз меньше множителя при (Y2—np2)2. Таким образом, следует заменить (3) на следующую формулу:
V= Определенную таким образом величину V называют статистикой c2, соответствующей значениям Y2, ..., Y12 полученным в эксперименте. Подставляя в эту формулу значения из (2), получаем V= Теперь, естественно, возникает вопрос, является ли значение Предположим, что все возможные результаты испытаний разделены на k категорий. Проводится п независимых испытаний: это означает, что исход каждого испытания абсолютно не влияет на исход остальных. Пусть рs,—вероятность того, что результат испытания попадет в категорию s, и пусть Ys,—число испытаний, которые действительно попали в категорию s. Сформируем статистику
В предыдущем примере имелось 11 возможных исходов при каждом бросании костей, так что ^==11. [Формулы (4) и (6) различаются только нумерацией: в одном случае она производится от 2 до 12, а в другом—от 1 до k.] Используя тождество (Ys—nps)2=Y2s—2npsYs+-n2p2s и равенства Y1,+Y2,+...+Yk = n, p1+p2+...+pk = 1, (7) можно преобразовать формулу (6) к виду
причем в большинстве случаев такая запись облегчает вычисления. Вернемся к вопросу о том, какие значения V можно считать разумными. Ответ на это дает табл. 1, в которой приведено "распределение c2 с v степенями свободы" при разных значениях v. Следует пользоваться строкой таблицы с v=k—1; число "степеней свободы" равно k—1, т. е. на единицу меньше числа категорий. Таблица 1 Некоторые данные для распределения c2
(На интуитивном уровне это можно пояснить следующим образом: значения Y1, Y2, ..., Yk не совсем независимы, так как Y1согласно (7), можно вычислить, зная Y2, ...,Yk. Следовательно, имеется k—1 степеней свободы. Более строгая аргументация будет приведена ниже.) Если в таблице в строке v и колонке р находится число x, то это означает, что значение V, определяемое по формуле (8), будет больше х с вероятностью р. Например, для р=5% и v==10 таблица дает значение x==18.31; это означает, что V> 18.31 только в 5% всех случаев. Предположим, что описанный процесс бросания костей моделируется на ЭВМ с помощью последовательности чисел, которые предполагаются случайными, и что получены следующие результаты s = 2 3 4 5 6 7 8 9 10 11 12 Эксперимент 1 Ys= 4 10 10 13 20 18 18 11 13 14 13 Эксперимент 2 Ys= 3 7 11 15 19 24 21 17 13 9 5 (9) Вычисляя статистику критерия c2, получаем в первом случае V1=29 59/120, а во втором случае V2=1 17/120. Табличные значения, соответствующие 10 степеням свободы, показывают, что V1 явно слишком велико; V бывает больше, чем 23.2, только в одном проценте случаев! (Более полные таблицы показывают, что вероятность появления столь большого значения V равна 0.1%.) Таким образом, в эксперименте 1 зарегистрировано значительное отклонение от нормы. С другой стороны, V2 очень мало, потому что Ys в эксперименте 2 оказались очень близки к средним значениям nps,[ср. с(2)]. Из таблицы распределения c2 следует, что в 99% случаев V должно быть больше, чем 2.56. Значение V2 явно слишком мало; полученные в эксперименте значения Vs настолько близки к средним значениям, что невозможно считать этот эксперимент случайным испытанием. (В самом деле, из более полных таблиц следует, что при 10 степенях свободы такие низкие значения V встречаются только в 0.03% случаев). Наконец, с помощью таблицы распределения c2 можно проверить полученное нами в (5) значение V==77/48. Оно попадает в интервал между 75 и 50%, так что мы не можем считать его слишком высоким или слишком низким; данные, представленные в (2), удовлетворяют критерию c2. Большим преимуществом рассматриваемого метода является , тo, что одни и те же табличные значения используются при любых n и любых вероятностях рs. Единственной переменной является v = k-1. На самом деле приведенные в таблице значения не являются абсолютно точными во всех случаях: это приближенные. значения, справедливые лишь при достаточно больших угнанениях п. Как велико должно быть n? Достаточно большими можно считать такие значения п, при которых любое из прs не меньше 5; однако лучше брать п значительно большими, чтобы повысить надежность критерия. Заметим, что в рассмотренных примерах мы брали n =144, и np2 равнялось всего 4, что противоречит только что сформулированному правилу. Единственная причина этого нарушения кроется в том, что автору надоело бросать кости; в результате числа из таблицы оказались не очень входящими для нашего случая. Было бы гораздо лучше прорти эти эксперименты на машине при n= 1000 или 10 000, или даже 100 000. На самом деле вопрос о выборе п не так прост. Если бы кости были действительно неправильные, это проявлялось бы при сколь угодно больших. Но при больших значениях п могут сглаживаться локальные отклонения, такие, как следующие друг за другом блоки чисел с сильным систематическим смещением в противоположные стороны. При действительном бросании костей этого можно не опасаться, так как все время используются одни и те же кости, но если речь идет о последовательности чисел, полученных на ЭВМ, то такой тип отклонения от случайного поведения вполне возможен. В связи с этим желательно проводить проверку с помощью критерия c2 при разных значениях п, но в любом случае эти значения должны быть довольно большими. Итак, проверка с помощью критерия c2 заключается в следующем. Проводится п независимых испытаний, где п—достаточно большое число. (Следует избегать применения критерия c2 в случаях, если испытания не независимы; см., например, случай, когда одна половина событий зависит от другой.) Подсчитывается число испытаний, результат которых относится к каждой из k категорий, и по формулам (6) или (8) вычисляется значение V. Затем V сравнивается с числами из табл. 1 при v=k—1. Если V меньше значения, соответствующего р==99%, или больше значения, соответствующего р=1 %, то результаты бракуются как недостаточно случайные. Если р лежит между 99 и 95% или между 5 и 1%, то результаты считаются "подозрительными"; при значениях р, полученных интерполяцией по таблице, заключенных между 95 и 90% или 10 и 5%, результаты "слегка подозрительны". Часто с помощью критерия c2 проверяют по крайней мере три раза разные части исследуемого ряда чисел, и, если не менее двух раз из трех результаты оказываются подозрительными, числа отбрасываются как недостаточно случайные.
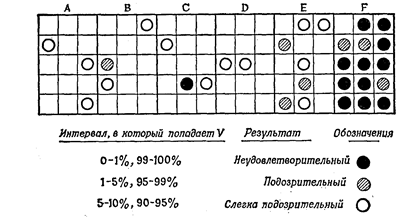
Рис. 14. ( Результаты 90 проверок с использованием критерия c2).
Рассмотрим в качестве примера рис. 14, где схематически представлены результаты проверки с помощью критерия c2 шести последовательностей случайных чисел. Для каждой последовательности делалось пять разных проверок (основанных на критерии c2), каждая из которых повторялась на трех разных участках последовательности. В датчике А использован метод Макларена—Марсальи (алгоритм 3.2.2М), в датчике Е—метод Фибоначчи, остальные датчики соответствуют линейным конгруэнтным последовательностям со следующими параметрами: ДатчикВ: Хо==0, а =3,141592653, с=2718281829, т=235 Датчик С: Х0=0, a=27+l, с=1, n==235. Датчик D: Хо= 47594118, a=23, c==0, т=108+1. Датчик F: Хо= 314159265, a=218+1, c=l, т=235. Результаты, приведенные на рис. 14, позволяют сделать следующие выводы. Датчики А, В, D прошли испытания удовлетворительно, датчик С находится на грани и должен быть, по-видимому, забракован, а датчики Е и F определенно не прошли испытаний. Датчик F1, безусловно, маломощен; датчики С и D обсуждались в литературе, но у них слишком мало значение а. В датчике D реализован метод вычетов в том виде, в каком он был впервые предложен Лемером в 1948 г., а в датчике С—линейный конгруэнтный метод с с¹0 также в его первоначальном виде (Ротенберг, 1960). Несколько другой подход к суждению о результатах проверки по критерию c2, без использования таких понятий, как "подозрительный", "слегка подозрительный" и т. д., и менее позволяющий полагаться на мнение ad hoc, описывается монографии [3]. Заключительная часть Таким образом, в результате рассмотрения учебных вопросов лекции нами был изучен ряд наиболее важных элементов используемых при построении специальной аппаратуры: датчики чисто случайных последоватекльностей (ЧСП), и датчики псевдослучайных последовательностей (ПСП) - ЛРР. Почти на каждом занятии при изучении узлов аппаратуры вам будут встречаться ЛРР. Поэтому для понимания процессов протекающих в изучаемых узлах, необходимо в совершенстве знать принципы построения, математическое описание и особенно свойства ЛРР. Кроме того, рассмотрен алгоритм проверки последовательностей на случайность. В частности, на соответствие двоичной последовательности биномиальному закону распределения.
Использованная для подготовки к лекции литература: 1.А.П.Баранов, Н.П.Борисенко, П.Д.Зегжда, С.С.Корт, А.Г.Ростовцев Математические основы информационной безопасности - ВИПС, Орел 1997 2. N. Koblitz. A Course in Number Theory and Cryptography.- Springer, GTM 114, 1987. 3. Д.Кнут, Искусство программирования для ЭВМ. Т. 2 «Мир», М.: 1977
Председатель ПМК (старший преподаватель)
" "________________ 2000 г. |



 . (4)
. (4) (5)
(5) настолько большим, что его случайное появление можно считать маловероятным. Прежде чем отвечать на этот вопрос, сформулируем критерий c2 в более общем виде.
настолько большим, что его случайное появление можно считать маловероятным. Прежде чем отвечать на этот вопрос, сформулируем критерий c2 в более общем виде. (6)
(6)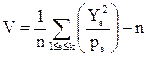 (8)
(8)