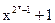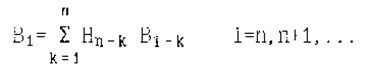ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Неприводимый полином называется примитивным, если он делит без остатка многочлен
и не делит ни один многочлен вида xк+1 где к<2n-1 Для каждой степени n имеется хотя бы один примитивный полином. В настоящее время построены таблицы неприводимых примитивных полиномов. Если h(x) примитивный, то примитивным является и двойственный ему полином h*(x). Таким образом, в результате изучения учебного материала по первому вопросу были рассмотрены определение, обобщенная схема и процесс формирования выходной последовательности ЛРР. Было показано, что любой ЛРР можно математически описать с помощью характеристических полиномов h(x). Проведенный анализ выходной последовательности формируемой ЛРР, выявил ряд интересных свойств, наиболее важные из которых рассмотрим во втором вопросе лекции. CВОЙСТВА ЛРР 1. Свойство детерминированности. Символы выходной последовательности ЛРР начиная с n-ого такта полностью определяются своими предыдущими значениями. Это вытекает из рекуррентного соотношения
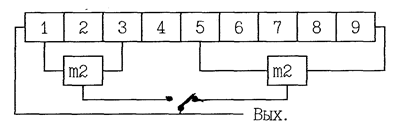
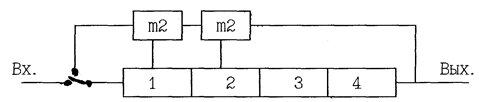
2. Период рекуррентной последовательности. Это время, по истечении которого повторится исходное состояние ЛРР. Период ЛРР зависит от полинома, на основе которого он строится. Максимальным периодом обладают ЛРР построенные на примитивных полиномах. Определим максимальный период ЛРР. Если число разрядов ЛРР = n , то максимально возможное число состояний разрядов ЛРР равно mn=2n Учитывая, что одно состояние ЛРР является запрещенным, получаем Т=2n-1 3. Cвойство группового сложения. Почленная сумма по модулю два любых двух выходных последовательностей одного ЛРР, получаемых при разных начальных заполнениях, является выходной последовательностью этого же ЛРР с другим начальным заполнением. Это начальное заполнение равно сумме исходных начальных заполнений. Например для ЛРР изображенного на рис.2 имеем 001 1 0 0 1 0 1 1 110 0 1 1 1 0 0 1 111 1 1 1 0 0 1 0 4.Свойство сдвига. Циклический сдвиг выходной последовательности ЛРР есть его же выходная последовательность при другом начальном заполнении. 1110010111001 0101110011110 5.Свойство баланса. Любая последовательность максимального периода содержит 2n-1 единиц и 2n-1-1 нулей. 6.Свойство окна. Если по выходной последовательности максимальной длины перемещать " окно" шириной n элементов, то на периоде ЛРР каждая из возможных комбинаций длины n будет зафиксирована только один раз. 7.Свойство серий. Определим серию, как последовательность одинаковых элементов. Любая выходная последовательность максимальной длины имеет: -половину всех серий длины в 1 знак -четверть всех серий длины в 2 знака -одну восьмую всех серий длины в 3 знака и так далее, пока доли дают целое число. длина 1----------4 длина 2----------2 длина 3----------1 длина 4----------1 всего серий -----8 Если известна степень примитивного полинома n, но неизвестны его коэффициенты, то они могут быть однозначно определены по любым 2n смежным элементам его выходной последовательности. Поиск коэффициентов hi, i=1,..n-1 характеристического полинома сводится к решению системы n однородных линейных уравнений с n неизвестными. Это потребует порядка n3 операций типа сложения, умножения. Существуют алгоритмы проверки любой двоичной последовательности на рекуррентность. Эти алгоритмы позволяют найти коэффициенты полинома h(x) при неизвестной длине ЛРР. В настоящее время известны несколько десятков свойств ЛРР. Выше перечисленные являются важнейшими из них. Рассмотренные выше свойства ЛРР легли в основу широкого применения их для построения цифровых узлов техники связи. Изучению конкретных узлов специальной аппаратуры, в основу построения которых положены ЛРР и их свойства, посвятим третий учебный вопрос. ПРИМЕНЕНИЕ ЛРР Благодаря уникальным свойствам, ЛРР нашли широкое применение в специальной аппаратуре. На их основе строятся: - Формирователи квазислучайной импульсной последовательности; - Датчики временных интервалов (счетчики с произвольным целым коэффициентом деления); - Схемы кодирования и декодирования помехоустойчивых кодов; - Установление синхронизма между взаимодействующими на канале связи аппаратами. Детерминированность процессов в ЛРР, хорошие статистические свойства последовательности максимальной длины (ПМД) позволили использовать ЛРР в качестве источников квазислучайной импульсной последовательности. Они используются в специальной технике в качестве: датчиков испытательных сигналов (ДИС). В качестве ДИС в соответствии с МККТТ используется ЛРР с n=9. По своим свойствам выходная последовательность приближается к рабочему сигналу. По испытательному сигналу осуществляется проверка достоверности передаваемой информации перед вхождением в связь, а при необходимости и корректировка канала связи. Схема ДИС реализованого в аппаратуре имеет вид изображенный на рис.9. ЛРР с n=3 используются для поиска неисправностей в аппаратуре, так как при таком периоде повторения сигнал легко наблюдать на осциллографе. С помощью такого ДИС производится испытание цифровых каналов. В вокодерах для синтеза шумовых звуков в качестве сигнала возбуждения используется шумовой сигнал. В некоторых типах вокодеров этот сигнал формируется с помощью ЛРР.
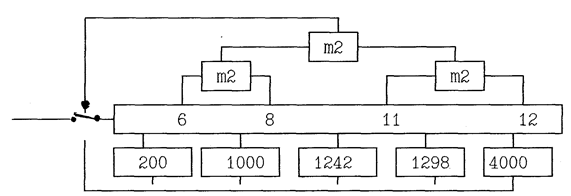
Рис.9 В соответствии со свойством детерминированности состояния ЛРР изменяются в строго определенном порядке. Если произвести начальную установку разрядов ЛРР, то можно точно определить их состояние на любом такте работы. Данный принцип положен в основу построения счетчиков с произвольным целым коэффициентом деления, датчиков временных интервалов(временных распределителей). Такой счетчик(датчик) состоит из ЛРР, схемы установки исходного состояния и анализаторов. На рисунке 10 показан датчик временных интервалов, который формирует команды на 200,1000,1242,1298 и 4000-ом тактах работы.
Рис.10 С помощью ЛРР производится умножение и деление многочленов. Эти операции выполняются при помехоустойчивом кодировании. Формирование кода 7.4 показано на рисунке 11.
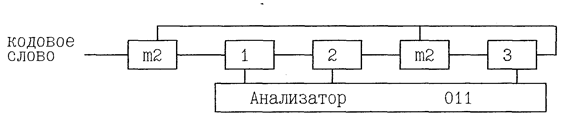
Рис.11 Деление кода 7.4 поступающего с канала связи с помощью ЛРР представлено на рисунке 12.
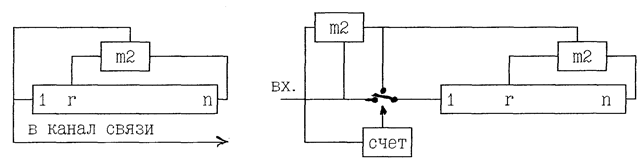
Рис.12 Синхронизация взаимодействующих на канале связи аппаратов осуществляется путем передачи синхронизирующей посылки (СП), которая представляет собой выходную последовательность ЛРР. Для приема этой последовательности на приеме устанавливается точно такой же ЛРР, однако работает он в режиме приема СП с отключенной обратной связью. Если последовательность приходит с канала связи без искажений, то после поступления n элементов , в цепи обратной связи обоих ЛРР будет формироваться одна и та же последовательность. Контроль за идентичностью последовательностей осуществляет сумматор по модулю два. Результат сравнения подсчитывается счетчиком. Как только счетчик заполниться, формируется команда на перевод ЛРР в автономный режим работы (включение обратной связи ЛРР). Синхронизация по вышеприведенному принципу получила название метода зачетного отрезка (ЗОТ). Схема поясняющая указанный принцип синхронизации показана на рисунке 13.
Рис.13 Минимальная длина безошибочно принятой последовательности, при которой ЛРР переходит в автономный режим работы, называется зачетным отрезком. Величина его равна n0=n+m где:n-длина ЛРР; m-емкость счетчика. |