 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Оценка математического ожидания нормального распределения
Точечные оценки При помощи частот либо гистограммы можно судить( хотя бы примерно) о характере распределения наблюдаемой случайной величины. Однако часто интерес представляют численные характеристики распределения – математическое ожидание, дисперсия и др. Это обусловлено тем ,что в процессе принятия решения удобнее опираться на небольшое число значимых параметров. В связи с этим возникает задача: исходя из набора значение(выборки) Х1,Х2….,Хn Величины Х, полученного в результате n независимых наблюдений, оценить значение математического ожидания EX, дисперсия DX либо еще какого-нибудь параметра. Пока наши рассуждения носят общий характер, мы будем обозначать оцениваемый параметр буквой θ(тэта). Повторим сказанное иными словами(реализация) которой Х1,Х2….,Хn каким- либо образом становится нам известными. (Этой случайной величиной может быть число посетителей данного магазина в течении дня, рост в сантиметрах студента данного вуза, головой доход гражданина данной страны и пр.) У величины Х имеется, скажем, математическое ожидание, которое нам неизвестно. Требуется найти способ, при помощи которого по известным реализациям величины Х модно разумным образом оценить неизвестное математическое ожидание. Сейчас мы рассмотрим, каким образом неизвестный параметр оценивается одним числом. такая оценка называется точечной. Любая оценка для θ- обозначаем ее θ—будет представлять собой некоторое выражение, составленное из символов Х1,Х2….,Хn:
Тем самым Замечание. Подчеркнем, что на момент принятия решения о значении параметра Пример 1.Студент размышляет , ехать ли ему домой или идти в библиотеку. Ненаходя решающих аргументов в пользу того или другого, он решает провести испытание - подбросить монету, и если выпадет герб, то ехать домой( в противном случае- идти в библиотеку).В сущности, решение тем самым принято( определен алгоритм действий).Однако до подбрасывания монеты неизвестно, что же выпадет, герб или цифра(соответственно неизвестно и направление дальнейших передвижений студента). Естественно предъявить к оценке 1) Желательно, чтобы при использовании величины
Оценка, удовлетворяющая такому условию, называется несмещенной. 2) Желательно, чтобы с увеличением числа n опытов значение случайной величины
(дисперсия оценки стремится к нулю при неограниченном возрастании числа наблюдений). Оценка, удовлетворяющая такому условию, называется состоятельной. Рассмотрим важный пример- точечную оценку для математического ожидания EX. Таким образом, в данном случае θ= EX. В качестве такой оценки примем так называемое эмпирическое среднее, т.е. среднее арифметическое величин Х1,Х2….,Хn:
Случайные величины Х1,Х2….,Хn имеют один и тот же закон распределения, совпадающий с законом распределения величины Х. Поэтому
Таким образом, оценка
Выражение DX/n, очевидно, стремится к нулю при неограниченном возрастании n. Отсюда вытекает состоятельность Соотношения Понадобятся нам в дальнейших рассмотрениях. Интервальные оценки Рассмотренная в предыдущем пункте точечная оценка часто бывает достаточной для практических выводов. Однако если есть необходимость в более детальном анализе, то надо оценить, насколько истинное значение параметра расходится с точечной оценкой этого значения. В этом случае можно поступить следующим образом. Выберем интервал(θ1,θ2) таким образом, чтобы вероятность включения в этот интервал параметра θ была достаточно велика ( близка к единице). Говоря более строго, это означает , что вероятность выполнения двойного неравенства θ1(Х1,Х2….,Хn)<θ< θ2(Х1,Х2….,Хn) не меньше заданного числа Вероятность Рассмотренная оценка называется интервальной. Еще раз подчеркнем, что интервальная оценка зависит не только от имеющихся данных, но и от требуемой надежности Методы построения интервальных оценок будут обсуждаться в последующих разделах. Сейчас же приведем неформальный пример, поясняющий различие точечной и интервальной оценок. Когда о каком либо человеке говорят: « ему примерно 38 лет», это ни что иное, как точечная оценка возраста. Когда же говорят:» Ему лет 35-40», это интервальная оценка, доверительный интервал-(35;40).Надежность оценки при этом в явном виде не указывается, но предполагается довольно близкой к единице. Иногда можно слышать и высказывания такого рода: «Ему лет 35-40, по крайней мере не больше 45». Очевидно что доверительный интервал (35;45) имеет большую доверительную вероятность, чем интервал (35;40). Однако интервальная оценка(35;40) более информативна, чем оценка (35;45). Оценка математического ожидания нормального распределения В этом разделе мы рассмотрим конкретный пример построения точечной и интервальной оценок. И здесь, как и раннее, исходными данными являются результаты наблюдений Х1,Х2….,Хn Кроме того, известно, что эти числа являются реализациями нормальной случайной величины N( μ , Далее вопрос может быть поставлен различными способами: Требуется оценить неизвестный параметр μ; Требуется оценить неизвестный параметр s w:val="28"/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Известен параметр s w:val="28"/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Из перечисленных трех задач мы рассмотрим лишь одну- последнюю. Итак, требуется найти точечную и интервальную оценки математического ожидания μ случайной величины Х, распределенной по нормальному закону с известным стандартным отклонением s w:val="28"/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Точечная оценка Точечную оценку
Как уже отмечалось , такая оценка является несмещенной и состоятельной для любой случайной величины, в том числе, разумеется, и в данном случае. Интервальная оценка Для построения интервальной оценки необходимо сначала выбрать доверительную вероятность Справедливо следующее утверждение: сумма независимых случайных величин, каждая их которых распределена по нормальному закону, также распределена по нормальному закону. Отсюда вытекает, что величина Выше было показано(см.(1)), что
Применительно к данному случаю имеем: Так что Рассмотрим случайную величину
Ее распределение является нормальным с математическим ожиданием 0 и дисперсией 1. Пользуясь этим обстоятельством, можно по данному
(площадь области, заштрихованной на рис.1, равна
Замечание. индекс Справедливо равенство
Напомним, что функция Ф(х) служит для вычисления вероятностей, связанных с нормальным распределением. Таблица ее значений имеется в приложении ( в конце книги). Для нахождения числа
Число Получив Или, более подробно,
равна
Таким образом, с доверительной вероятностью
Число Называется погрешностью оценки математического ожидания. С доверительной вероятностью
При этом, разумеется, n должно быть целым числом. Так как сбор данных часто связан с некоторыми затратами, обычно берут минимальное целое n, удовлетворяющее неравенству(5). Пример 2. При измерении нормальной случайной величины со стандартным отклонением, равна 5, и неизвестными математическим ожиданием μ получена следующая выборка: 3,12,8,14,15,6,19,10,15,6. Требуется найти:1) интервал, содержащий параметр μ с доверительной вероятностью В данном случае s w:val="28"/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> Для точечной оценки получаем
Решим уравнение Для этого следует найти число 0,475 или ближайшее к нему в таблице среди значений функции ф(х)( таблица дана в приложении). Ближайшее число -0,477. Соответствующее этому значению аргумента
Теперь осталось воспользоваться формулами (2) и (3), подставив туда в условии s w:val="28"/></w:rPr><m:t>Пѓ</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
Таким образом ,искомым доверительным интервалом является интервал(7,64;13,96). Для погрешности ɛ получаем следующее значение:
14.4 Оценки вероятности события Пусть некоторое событие происходит в результате единичного испытания с вероятностью P , которая нам неизвестна однако ситуация позволяет многократно повторить испытание и подсчитать , сколько раз произошло указанное событие. Более точно : пусть произведено n испытаний, в которых событие произошло m раз . Здесь в отличие от предыдущих рассмотрений исходными данными для анализа будут всего два числа – n и m.
Точечная оценка Не вызывает сомнений, что точечная оценка
Докажем несмещенность и состоятельность этой оценки. При любом фиксированном n величина m является случайной величиной с биноминальным законом распределения:
Напомним, что в этом случае
Докажем несмещенность оценки
Теперь вычислим величину
Таким образом, Что доказывает состоятельность точечной оценки Интервальная оценка Для построение интервальной оценки вспомним ( см. формулу (2) на с. 262), что биномиальная случайная величина
Пользуясь этим обстоятельством , можно найти границы доверительного интервала
где
Пример 3. Из 200 случайным образом отобранных изделий не который фирмы 10 оказались бракованными. Найти доверительный интервал, содержащий с надёжностью Решение. Здесь
Примерная формула (9), (6), (7), (8), получаем, что
(напомним, что это значение находится по таблице),
(это точечная оценка),
Таким образом , доверительный интервал оказался следующим : (0,01; 0,09) . Иными словами, с доверительной вероятностью 0,99 доля бракованных изделий лежит в промежутке 1% и 9%. |





 является несмещенной. Дисперсия этой оценки вычисляется следующим образом:
является несмещенной. Дисперсия этой оценки вычисляется следующим образом:
 ).
). ;
; параметра μ определим как эмпирическое среднее:
параметра μ определим как эмпирическое среднее:
 распределена по нормальному закону.
распределена по нормальному закону.
 ).
). .
.
 Из формулы (4)видно что с ростом числа данных n погрешность становится все меньше, т.е. доверительный интервал сужается. В свою очередь, чем меньше погрешность, тем больше данных необходимо собрать для ее достижения. Если требуется погрешность ɛ задана, то найти соответствующий оббьем данных:
Из формулы (4)видно что с ростом числа данных n погрешность становится все меньше, т.е. доверительный интервал сужается. В свою очередь, чем меньше погрешность, тем больше данных необходимо собрать для ее достижения. Если требуется погрешность ɛ задана, то найти соответствующий оббьем данных:  =10.8
=10.8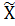 ,
, 
 Задача, которую мы будем рассматривать, заключается в отыскании оценки неизвестной вероятности P по имеющимся данным n, m и доверительной вероятности
Задача, которую мы будем рассматривать, заключается в отыскании оценки неизвестной вероятности P по имеющимся данным n, m и доверительной вероятности вероятности P определяется следующим соотношением :
вероятности P определяется следующим соотношением : . (6)
. (6)

 . Имеем :
. Имеем :

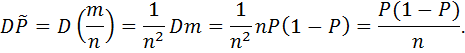

 может быть приближена нормальной случайной величиной
может быть приближена нормальной случайной величиной  и
и  (эти условия будем далее считать выполненными). Поэтому можно считать, что
(эти условия будем далее считать выполненными). Поэтому можно считать, что
 методом, сходным с методом вычисления доверительного интервала для математического ожидания нормального распределения. Выпишем сразу результат :
методом, сходным с методом вычисления доверительного интервала для математического ожидания нормального распределения. Выпишем сразу результат : (7)
(7) (8)
(8) - решение уравнения
- решение уравнения (9)
(9) долю бракованных изделий среди всей продукции фирмы .
долю бракованных изделий среди всей продукции фирмы .




