 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Проблема строения атома. Опыты Резерфорда 12
1.Закономерности в спектрах атомного водорода. В 1885 г. швейцарец Иоганн Бальмер исследовал спектр водорода. Оказалось, что в электрическом разряде при давлении не более 10 мм Hg большинство молекул водорода диссоциируют на атомы. Спектр, испускаемый атомами водорода, становится более заметным по сравнению с молекулярным. Измерив длины волн λ спектральных линий, Бальмер нашёл, что они укладываются в формулу:
Здесь m = 3, 4, 5, ... ∞ – натуральное число, R – коэффициент пропорциональности, называемый постоянной Ридберга, R = 1,097·107 м–1. Бальмеру удалось наблюдать 4 линии: Hα (m = 3), λ = 656,3 нм, красная; Hβ (m = 4), λ = 486,1 нм, сине-зелёная; Hγ (m = 5), λ = 434,0 нм, фиолетовая; Hδ (m = 6), λ = 410,2 нм, фиолетовая. Наблюдать большее число линий в спектре, получаемом с помощью разрядной трубки, трудно по той причине, что газ в трубке сильно разрежён. С целью повышения интенсивности исследуемый пучок света стали формировать вдоль разрядной трубки, увеличивая её длину до 1-2 м. В 1920 г. Роберт Вуд сфотографировал 22 линии серии Бальмера. Максимальное число линий, 37, удалось сфотографировать в спектре солнечной короны. Здесь водород очень разрежён, поэтому газ находится исключительно в атомном состоянии. Но за счёт гигантской протяжённости короны интенсивность света достаточно высокая. Соответствие формулы эксперименту поразительно. Расхождение в значениях вычисленных и измеренных λ появляются лишь в 5-6 знаке. На рис.1
показано расположение линий серии Бальмера в спектре. Примерно так выглядит атомный спектр водорода в спектрометре с дифракционной решёткой. С ростом m линии серии располагаются всё теснее. Минимальная длина волны серии λ = 364,7 нм при m = ∞ называется границей серии. В 1906 г. американец Теодор Лайман нашёл подобную серию в ультрафиолетовой области спектра, удовлетворяющую формуле:
Все серии объединяются одной обобщённой формулой
где n = 1, 2, 3, ..., m = n + 1, n + 2, n + 3, ... ∞. В зависимости от значения n получается та или иная серия. n = 1, Серия Лаймана, λmax (m = 2) = 121,6 нм, λmin (m = ∞) = 91,2 нм. УФ обл. n = 2, Серия Бальмера (656,3 – 364,7 нм). Видимая область. n = 3, Серия Пашена (1875 – 820 нм). Ближняя ИК-область. n = 5, Серия Пфунда (7458 – 2278 нм). Дальняя ИК-область. В спектре поглощения водорода, атомы которого не возбуждены, присутствует только серия Лаймана. Это объясняется тем, что большинство атомов водорода находятся в основном состоянии, которое соответствует n = 1. (См. след. параграф).. 2.Проблема строения атома. Механическая модель атома как неизменной частицы материи в конце 19 века пришла в прямое противоречие с физическим опытом. В 1887 г. был открыт фотоэффект (выбивание светом из вещества электронов, Г. Герц), в 1895 г. Вильгельм Рентген открывает X-лучи (испускание ЭМ-волн электронами при их быстром торможении о метал), в 1896 г. Антуан Беккерель открывает естественную радиоактивность (испускание атомами проникающего излучения). Стало очевидно, что атом вещества имеет сложную структуру. Встал вопрос: что такое атом и как он устроен? 3.Модель атома Томсона. В 1897 г. Дж. Дж. Томсон, исследуя разряд в разрежённых газах, установил, что от катода к аноду движутся отрицательно заряженные частицы, масса которых примерно в 2000 раз меньше массы атома водорода. Так был открыт электрон. В 1904 г. Томсон предложил первую атомную модель, пригодную для количественных оценок. Согласно Томсону, атом представляет собой протяжённый шар радиусом R с равномерно и непрерывно распределёнными в нём положительным зарядом. Электроны, входящие в состав атома, находятся внутри этого заряженного шара. Суммарный заряд электронов равен заряду шара, поэтому атом в целом электронейтрален. Из модели Томсона вытекал простой механизм излучения атома водорода. Очевидно, заряд шара атома водорода e+, в нём должен находиться один электрон с зарядом e–. В невозбуждённом атоме электрон должен находиться в центре шара (рис. 3).
Если электрон сместить из центра на расстояние r, то на него будет действовать электрическая возвращающая сила, равная
Здесь Возвращающая сила квазиупругая, она пропорциональна смещению r электрона от центра шара. Под действием этой силы электрон способен совершать гармонические колебания x = Acosω0t, где Ускорение, испытываемое электроном, равно Итак, атом водорода по Томсону способен излучать лишь одну монохроматическую ЭМ-волну с частотой ω0. Он не может давать спектральную серию с бесконечным числом длин волн. Кроме того, модель Томсона не объясняет периодических свойств элементов в таблице Менделеева, природу химической связи, не объясняет α-распад и так далее. 4.Опыты Леонарда. В 1893 г. Филипп Леонард, изучая катодные лучи, впервые вывел отрицательно заряженные частицы (электроны), движущиеся в разрядной трубке от катода к аноду, через специальное окошко в воздух (рис. 4). Окошко Леонарда представляло собой тонкий листок алюминия толщиной 2-3 мкм. Чтобы листок не продавило атмосферным воздухом, он наклеивался на пластинку с отверстиями. Вылетавшие из разрядной трубки электроны улавливались цилиндром электрометра. Изменяя расстояние l между трубкой и электрометром, можно оценить характер поглощения электронов молекулами воздуха. Оказалось, что электронный пучок ослабляется в воздухе по закону Бугера
где S0 – эффективное сечение молекул воздуха, рассеивающих электроны, N0 – концентрация молекул. Скорость v электронов определяется напряжением U между катодом и анодом и находится из условия:
Изменяя напряжение на разрядной трубке, Ленард установил, что эффективное сечение молекул воздуха S0 быстро уменьшается с ростом скорости движения электронов. После продолжения и углубления опытов в 1903 г. Ленард делает вывод: масса атома He распределена равномерно по его объёму. Она занимает малую часть его объёма. 5.Опыты Резерфорда. В 1909 г. Эрнст Резерфорд с целью уточнения размеров атомов провели серию опытов. В качестве частиц-снарядов они использовали не электроны, легко отклоняющиеся в электромагнитных полях, а тяжёлые α-частицы – двукратно ионизированные атомы гелия. В отличие от отрицательных ионов α-частицы несут положительный заряд, и потому должны отталкиваться от положительно заряженного ядра атома. Масса α-частицы примерно в 8000 раз больше массы электрона. Установка представляла собой гониометр, на оси которого крепился листок золотой фольги Au (рис. 5).
Под прямым углом к плоскости фольги на некотором расстоянии от неё находился контейнер с препаратом α-активного радия 88Ra226. Вокруг фольги с препаратом почти на полный оборот могла поворачиваться труба микроскопа М. В фокусе объектива микроскопа крепилась стеклянная пластинка с напыленным порошком сульфида цинка ZnS. При попадании α-частицы в кристалл ZnS происходила сцинтилляция – люминесцентная вспышка зеленоватого света, наблюдавшаяся в микроскоп М. Во избежание рассеяния α-частиц на молекулах газа установка герметизировалась и из неё откачивался воздух до давления p<1 мм Hg. Относительное положение препарата Ra и фольги оставалось в процессе Измерения сводились к подсчёту числа сцинтилляций при определённых углах θ за одинаковые промежутки времени. Всего было зарегистрировано (визуально!) около 150000 вспышек. В таблице 1.1 приведены результаты измерений рассеяния α-частиц золотой фольгой.
Прежде всего бросается в глаза, что подавляющее большинство α-частиц, взаимодействующих с фольгой, отклоняется в пределах 15º. опытов неизменным. И лишь ничтожно малая часть (0,05%) отражается под углами 135-150º. Резерфорд предположил, что эти α-частицы отражаются в результате единичных лобовых соударений с ядром. Для обработки результатов Резерфорд построил количественную теорию рассеяния α-частиц. При этом он полагал, что весь положительный заряд атома Ze+ сосредоточен в ядре, а электрическое взаимодействие внутри атома подчиняется закону Кулона. Результаты исследований были опубликованы в 1911 г. По характеру рассеяние α-частиц атомами металлов Резерфорд вычислил размер ядра. Его поперечник оказался в 10 000 раз меньше атома. Резерфорд предложил ядерную или т.н. планетарную модель атома. Атом состоит из ядра с зарядом Ze+ и вращающихся вокруг него по круговым орбитам z электронов. Электрическое поле ядра подчиняется закону Кулона. 7.Проблема устойчивости атома Резерфорда. В отличие от статической модели атома Томсона атом Резерфорда динамический. Каждый электрон атома движется вокруг ядра по круговой орбите так, что центростремительная сила равна кулоновской силе притяжения электрона к ядру.
Здесь me – масса электрона, r – радиус его орбиты, z – зарядовое число ядра, то есть количество в нём элементарных положительных зарядов. Поскольку атом нейтрален, то зарядовое число ядра z равно числу электронов в атоме. Если принять, что радиус атома водорода близок к радиусу атома золота, то есть r » 10–10 м, то скорость движения электрона в атоме водорода составляет около Но с учётом законов электродинамики планетарный атом неустойчив. Ведь электроны, движущиеся по окружностям, испытывают центростремительное ускорение.
Применительно к атому водорода Расчёты показывают, что вся энергия электрона перейдёт в энергию ЭМ волны за время Спектр ЭМ излучения, испускаемого электронами такого гибнущего атома, должен быть сплошным, а не линейчатым.
Атом Бора 1. Постулаты Бора. Принципиальный отказ от механической трактовки атома сделал датский физик Нильс Бор в 1913 г, когда он сформулировал два постулата. Постулат 1. Правило квантования орбит. Электроны в атоме могут находиться не на любых энергетических уровнях, допускаемых классической механикой. Они могут находиться лишь на определённых стационарных уровнях, на которых орбитальный момент импульса электрона L = mvr кратен величине h/2π.
Атом в стационарном состоянии не излучает и не поглощает энергии. Постулат 2. Правило частот. Переход электрона с одного уровня на другой сопровождается излучением или поглощением кванта энергии
Здесь Ek и Ei – энергия атома с электроном на k-том и i-том уровнях, νik – частота излучаемого или поглощаемого света при переходе электрона с одного уровня на другой. 2. Основания постулатов лежат в опытных фактах. Первый постулат, признающий существование в атомах стационарных энергетических уровней электронов. Поскольку атомы длительное время существуют, то существуют и их состояния, в которых атомы не излучают и не поглощают. То, что классическая электродинамика не может объяснить этот факт, следует рассматривать как ограниченность электродинамики, не применимость её законов для описания внутриатомных процессов. Основанием второго постулата являются фотоэффект, тепловое излучение и сериальные закономерности в спектре атома водорода. При фотоэффекте свет поглощается квантами hν. Из законов теплового излучения следует, что излучается свет также квантами hν. Но это значит, что и спектральные линии в излучении атома водорода формируются квантами с энергией hν. Если умножить формулу Бальмера (1.6) на hc, где с – скорость света в вакууме, то получаем:
Слева стоит энергия hν кванта излучаемого атомом света, а справа – разность каких-то двух величин с размерностью энергии. Можно предположить, что выражение Rhc/π2, где n = 1, 2, 3, 4, …, пропорционально энергии атома водорода в стационарных состояниях. В качестве обоснования условия квантования момента импульса электронов на стационарных уровнях в виде L = nh/2π отметим лишь, что именно при таком квантовании из теории Бора вытекает формула Бальмера. 3. Опыты Франка и Герца. Основное положение Бора о дискретности значений энергии атома доказали экспериментально немцы Джеймс Франк и Густав Герц в 1913-14 и 1919-20 годах. Их установка представляла собой эвакуированную лампу с внесённой в неё каплей ртути (рис. 6).
Лампа помещалась в печь. Изменяя температуру в печи, можно было менять давление ртутных паров в лампе. В большинстве опытов давление составляло от 1 до 30 мм Hg. Лампа включала в себя три электрода: катод К, сетку S и анод А. Батарея Бн обеспечивала регулируемый накал катода, батарея Б1 создавала ускоряющее напряжение U1 между катодом и сеткой. Батарея Б2 создавала тормозящее напряжение U2 между сеткой и анодом. Ток через пары ртути между сеткой S и анодом А измерялся гальванометром Г. Процесс измерений сводится к построению вольтамперной характеристики лампы. Постепенно увеличивалось напряжение U1 между катодом К и сеткой S и записывался ток i по гальванометру Г между сеткой S и анодом А при постоянном задерживающем напряжении Если бы в лампе был вакуум, то вольтамперная характеристика представляла бы собой монотонную кривую, показанную на (рис. 7.2)
При больших напряжениях U1>>U2 ток i стремится в вакууме к току насыщения, когда все испускаемые катодом электроны приходят на анод. В парах ртути на вольтамперной кривой появляются впадины, начинающиеся при напряжениях ускоряющего поля U1 = 4,9; 9,8; 14,7 вольт (рис. 7.2 ). Их можно объяснить так. До напряжения 4,9 В электроны испытывают лишь упругий удар с атомами ртути. Поскольку масса атомов ртути в 400 000 раз больше массы электронов, а тепловая скорость атомов ртути по сравнению со скоростью электронов пренебрежимо мала, то электроны сталкиваются с атомами как с неподвижной стенкой. Скорость электронов меняется лишь по направлению, но не по величине. При U1 > U2 кинетическая энергия электронов eU1 оказывается достаточной для преодоления задерживающего поля U2. С увеличением U1 всё большая часть испущенных катодом электронов попадает на анод. Ток растёт. Но вот при напряжении 4,9 В энергия электронов оказывается равной тому кванту энергия атома ртути, который необходим для перехода атома из одного стационарного состояния в другое. При этом напряжении возле сетки S возникает зона неупругих столкновений электронов с атомами. Электроны гасят свою скорость у самой сетки S и потому не могут пройти на анод А из-за тормозящего поля U2. Возникает первый спад тока i. С дальнейшим ростом U1 зона неупругих столкновений постепенно перемещается влево. Она оказывается посредине между катодом К и сеткой S при напряжении 9,8 В. Третий спад на кривой появляется при напряжении 14,7 В, когда у сетки S появляется третья зона неупругих столкновений. Из результатов опытов следовало, что атомы ртути поглощают лишь строго определённую порцию энергии, равную eΔU1 = 4,9 эВ. Поглотив эту энергию, атомы ртути должны перейти на более высокий энергетический уровень, иначе, должны возбудиться. Рано или поздно, возвращаясь в основное (не возбуждённое) состояние, атомы ртути должны сбрасывать эту энергию в виде кванта hν ЭМ волны. Фотографирование спектра излучения паров Hg показало, что при напряжении U1 > 4,9 В пары Hg действительно излучают УФ волну с λ = 253,7 нм. Если верны постулаты Бора, то энергия излучаемых фотонов hν равна энергии электронов при резонансном поглощении.
4. Радиусы разрешенных уровней. Рассмотрим основные параметры атома, построенного в соответствии с постулатами Бора. Будем говорить в общем случае о водородоподобном атоме, имеющем ядро с зарядом ze+, вокруг которого движется один электрон. Это, например, атом водорода, z = 1; однократно ионизированный атом гелия (ион гелия He+), z = 2; двукратно ионизированный атом лития (ион лития Li++), z = 3 и т.д. Электрон в атоме Бора движется вокруг ядра под действием кулоновских сил. В первом приближении можно считать, что масса ядра бесконечно велика по сравнению с массой электрона. В этом случае ядро остаётся неподвижным, а электрон движется по круговым орбитам. Уравнение его движения можно записать так:
Здесь Используя условие квантования момента импульса круговых орбит из первого постулата Бора получаем систему двух уравнений, содержащую теорию атома.
а. Радиусы разрешённых уровней энергии найдём, исключив из системы уравнений (2.5) и (2.6) скорость движения электрона v. Из второго уравнения
Здесь rn – радиус n-й орбиты, где n = 1, 2, 3, … Число n называют главным квантовым числом. При z = 1 и n = 1 получаем радиус самого низкого энергетического уровня атома водорода (боровский радиус)
Диаметр атома водорода в основном состоянии равен В атомной физике широко используется внесистемная единица длины ангстрём ( Для других водородоподобных ядер формулу для rn удобно записывать так:
Итак, радиусы rn разрешённых уровней в водородоподобных атомах растут по квадратичному закону с ростом номера n. В разных атомах они тем меньше, чем больше номер элемента z в таблице Менделеева. б. Скорость движения электронов на разрешённых уровнях найдём, подставив rn из формулы (2.7) в уравнение (2.6).
Чем выше уровень, тем меньше на нём скорость движения электрона. На первом боровском уровне атома водорода скорость электрона составляет На втором боровском уровне, n = 2, скорость в 2 раза меньше, в. Энергия атома на разрешённых уровнях слагается из кинетической энергии электрона Ek и потенциальной энергии En взаимодействия электрона с ядром. Кинетическую энергию можно выразить из уравнения движения (2.5).
Потенциальная энергия электрона в кулоновском поле ядра
Здесь Отсюда находится полная энергия атома.
Подставив сюда rn из (2.7), получаем:
Здесь me – масса электрона, n = 1, 2, 3, … – квантовое число. Электрон притягивается к ядру, поэтому полная энергия системы ядро-электрон отрицательна. С ростом n энергия атома, уменьшаясь по абсолютной величине, растёт. При Для графического отображения энергетических уровней атома обычно откладывают по вертикальной оси значения энергии En, отмечая их отрезками горизонтальных прямых. Система стационарных уровней атома на тонкой схеме принимает вид, показанный на рис. 8. Низший уровень (n = 1) с минимальным значением энергии атома является самым устойчивым. Это основное состояние атома. Для перехода атома на уровни n = 2, 3, 4, … атом должен получить извне соответствующую порцию энергии. Поэтому состояния с 5. Излучение атома водорода. Рассмотрим, как объясняет теория Бора сериальные закономерности в спектре атома водорода. Схема на рис.8
делает механизм излучения атома наглядным. Чтобы испускать квант энергии hν, электрон в атоме должен перейти с более высокого уровня на низкий. Для краткости говорят атом переходит с одного уровня на другой. При переходе атома водорода (z = 1) из состояния m в состояние n излучается фотон с энергией
Разделив на hc, получаем формулу Бальмера.
Если теоретические построения в теории Бора справедливы, то коэффициент перед скобками должен быть равен постоянной Ридберга. Из спектрологии (опыт) Вычисленное из (2.15) Совпадение R, вычисленного в теории, с опытом с точностью до 4-х знаков можно считать большим успехом теории Бора. Из энергетической диаграммы, показанной на становится понятным механизм появления спектральных серий. УФ серия Лаймана появляется при переходах атома водорода из любых возбуждённых состояний на низший энергетический уровень с n = 1. Здесь могут быть самые большие энергетические ступени, и потому самые малые длины волн λ. Серия Бальмера образуется при переходе возбуждённого атома на уровень n = 2. Энергетические ступени здесь уже меньше, поэтому серия Бальмера попадает в видимый диапазон. Энергетические ступени в сериях Пашена, Брэкета и Пфунда становятся ещё меньше. Поэтому каждая последующая серия уходит всё дальше в ИК диапазон. 3. Потенциалы возбуждения атома водорода – это те напряжения U электрического поля, в котором должен разогнаться электрон, чтобы его энергия оказалась равной кванту энергии, поглощаемой или излучаемой атомом.
Поскольку невозбуждённое состояние атома соответствует n = 1, то все потенциалы возбуждения вычисляются из формулы Бальмера для серии Лаймана. При n = 2 получаем 1-й потенциал возбуждения атома водорода.
При n = ¥ получается такой квант энергии, при поглощении которого электрон уходит из атома. Атом превращается в ион. Потенциал ионизации атома водорода U¥ = 13,6 В. 6. Магнитный момент электрона. Mагнетон Бора. Электрон – электрически заряженная частица. Поэтому наряду с механическим моментом Магнитный момент М кругового тока M = iS, где i – ток, протекающий по замкнутому витку, а S – площадь витка. Циркулирующий по круговой орбите электрон создаёт ток i = en = ev/2pr, где n – частота обращения электрона. Выразив скорость v орбитального движения электрона через механический момент импульса L, v = L/mer, и подставив, получаем: i = ev/2pr = eL/2mepr. Площадь «витка» S = pr2, где r – радиус орбиты. Отсюда орбитальный магнитный момент электрона
При n = 1 получаем минимальный магнитный момент электрона в атоме водорода в основном состоянии: 7. Достоинства теории Бора. Модель Бора была крупным шагом в развитии теории строения атома. Её достоинства: а. Объяснила сериальные закономерности в спектрах атома водорода. Вычисленная на её основе постоянная Ридберга для водорода с точностью до 4-х знаков совпадает с опытным значением. б. Объяснила сериальные закономерности в спектрах водородных атомов. Ещё в 1897 г. американский астроном Эдвард Пикеринг обнаружил в спектрах некоторых звёзд серию, напоминающую серию Бальмера, но немного смещённую в фиолетовую область спектра. Число линий в серии Пикеринга было больше, чем в серии Бальмера. Избыточные линии соответствовали дробным значениям числа n и не поддавались никаким объяснениям. Применение теории Бора показало, что серия Пикеринга принадлежит излучению однократно ионизированных атомов гелия и определяется формулой:
Смещение линий в фиолетовую область объяснилось тем, что постоянные Ридберга для гелия и водорода несколько отличаются из-за различия в массах ядер атомов. Исследование спектров двукратно ионизированного лития Li++ и трёхкратно ионизированного бериллия Be+++ показали, что и для них применима обобщённая формула Бальмера, а все сдвиги спектров объяснялись теорией Бора. в. Успехи теории Бора в объяснении спектра водородных и водородоподобных атомов показали, что классическая физика неприменима к описанию внутриатомных процессов. Теория Бора явилась толчком к большому числу экспериментальных работ, давших много важных результатов. 8. Недостатки теории Бора. Главные из них: а. Не позволяет определять интенсивность спектральных линий. Известно, что линии в спектрах имеют разную яркость. Очевидно, дело в том, что одни энергетические переходы в атомах совершаются относительно чаще, другие – реже. В результате в излучение одной спектральной линии уходит больше фотонов в излучение, другой – меньше. Но почему это происходит, теория Бора не даёт объяснения. б. Теория Бора не работает в атомах, следующих за водородом. Нет механизма формирования структуры атомов в таблице Менделеева. Теория Бора не объясняет природу химических связей. Не позволяет объяснить спектры многоэлектронных атомов. в. теория Бора логически противоречива. Она не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно – уравнение движения электрона – классическое, другое – условие квантования орбит – квантовое.
ВОЛНЫ ДЕ БРОЙЛЯ. 1. Волны де Бройля. К двадцатым годам 20-го столетия в физике окончательно утвердилось понимание того факта, что свет имеет двойственную природу. В таких явлениях, как интерференция, дифракция, поляризация свет ведёт себя как волна. А в явлениях фотоэффекта и эффекта Комптона свет ведёт себя как поток частиц. В корпускулярном проявлении каждая световая частица – фотон – характеризуется двумя величинами: энергией hν и импульсом hν/с. Если свет ведёт себя как волна, он описывается уравнением плоской монохроматической волны По мысли Де Бройля, каждой так называемой частице для описания её волновых свойств нужно поставить в соответствие некоторую волновую функцию ψ (как функцию Е, соответствующую фотону). Эта функция ψ (функция Де Бройля) также описывает плоскую монохроматическую волну, распространяющуюся в направлении скорости Импульс фотона
Чем больше импульс частицы, тем меньше его дебройлевская длина волны. Например, для электрона, ускоренного разностью потенциалов 100 В, λ = 0,12 нм, для протона при тех же условиях λ = 0,003 нм. Идею волновых свойств микрочастиц де Бройль использовал для объяснения правила квантования орбит в атоме Бора. Если движение электрона по орбите рассматривать как волну материи, распространяющуюся вокруг ядра в направлении движения электрона, то на стационарной орбите волна при обходе ядра будет всякий раз возвращаться в исходную точку с той же фазой и амплитудой.Условие квантования принимает вид:
Здесь r – радиус круговой орбиты электрона. 2. Дифракция электронных пучков в опытах Девиссона-Джермера. В 1927 г. американцы Клинтон Девисон и Лестер Джермер исследовали отражение электронов от монокристалла никеля. Установка включала в себя монокристалл никеля, сошлифованный, как показано на рис.
и установленный на держателе. На плоскость шлифа направлялся перпендикулярно пучок монохроматических электронов. Скорость электронов определялась напряжением U на электронной пушке: Под углом θ к падающему пучку электронов устанавливался цилиндр Фарадея, соединённый с чувствительным гальванометром. По показаниям гальванометра определялась интенсивность отражённого от кристалла электронного пучка. Вся установка находилась в вакууме. Металлический никель (Ni, z = 28, Mr = 58,7) может существовать в двух кристаллических модификациях (α и β). Если у кристалла срезать угол, как показано на рис. 10, то атомы в плоскости цилиндра приобретают ось симметрии 3-го порядка. Это значит, что при повороте кристалла на держателе (менялся азимутальный угол φ) через каждые 120° атомы в плоскости цилиндра принимали тождественное положение. Расстояние между атомами в плоскости шлифа равно Электроны, падающие на кристалл, при энергиях не более 80 эВ не проникают внутрь. Они отражаются от плоскости шлифа как свет от отражательной дифракционной решётки. Штрихи решётки формируются рядами атомов А1 А2 ... Расстояние между рядами (постоянная решётки) Опыты показали, что имеется ярко выраженная селективность рассеяния электронов. Первый максимум наблюдался при углах Пример: При напряжении на электронной пушке U = 54 В первый максимум интенсивности наблюдался под углом
Длина волны де Бройля для электронов равна
Гипотеза Де Бройля нашла опытное подтверждение. 3. Дифракция электронных пучков в опытах Дж. П. Томсона. В 1928 г. Джордж Паджет Томсон поставил опыт по дифракции электронных пучков при прохождении их через металлическую фольгу. Узкий моноэнергетический пучок электронов направлялся из электронной пушки на листок очень тонкой золотой фольги толщиной около 0,1 мкм. Чтобы электроны меньше поглощались и могли проходить сквозь фольгу, они разгонялись в электрическом поле с напряжением U в несколько десятков киловольт. Рассеянные на фольге электроны попадали на фотопластинку ФП (рис. 12, 1).
Опыты показали, что после проявления экспонированной в электронном пучке фотопластинки на ней появлялись концентрические тёмные кольца. Механизм их появления можно объяснить так. Полученная по обычной технологии из отливки и прокатанная золотая фольга состоит из множества мелких хаотично ориентированных кристалликов размером около 0,01 мкм. На пути электронного пучка оказывается множество граней таких кристалликов со всевозможной ориентацией. В одних случаях электрон проходит сквозь такой микрокристалл, в других – упруго отражается от него. В результате возникает хаотическое рассеяние электронов, создающее диффузное потемнение фотопластинки. Но в тех случаях, когда грань кристалла образует с осью падающего электронного пучка угол скольжения φ, соответствующий дифракционному максимуму по формуле Вульфа-Брэгга
где d – расстояние между атомными плоскостями, в направлении угла 2φ в рассеянном пучке реализуется дифракционный максимум (рис. 12, 2). Как и рентгеновские пучки электроны дифрагируют на атомных плоскостях, параллельных грани кристалла. В направлении угла 2φ на фотопластинке на фоне вялого диффузного потемнения образуется от грани кристалла интенсивное чёрное пятно. Множество таких кристалликов благодаря осевой симметрии относительно пучка АО образуют в статистике концентрические кольца (рис. 13). Если радиус кольца r, а расстояние от фольги до фотопластинки L, то, учитывая малость значений углов φ, можно записать равенство.
Изменяя напряжение U в электронной пушке, можно менять скорость электронов v и, тем самым, соответствующую электронам дебройлевскую длину волны λ. Радиус r кольца будет меняться. Но согласно (3.5), при сохранении геометрии установки неизменной (L = const) отношение r/λ для одного и того же кольца будет оставаться постоянным. Измерения показали, что отношение r/λ в опытах действительно сохраняется. В опытах Девиссона-Джермера использовались пучки относительно медленных электронов, которые разгонялись в поле напряжением U не более 100 В. Их скорость вычислялась по классической формуле eU = mv2/2 и не превышала 2% от скорости света. В опытах Томсона использовались пучки электронов высоких энергий
Например, в одном из опытов было U = 54,3 кВ. Скорость электронов, вычисленная по формуле (3.6), равна Для вычисления длины волны Де Бройля в формулу Поскольку электроны в опытах Томсона имеют энергию десятки кэВ, то при их торможении на фольге могут генерироваться рентгеновские лучи. Поэтому возникает опасение, что картина на фотопластинке образуется дифракцией Х-лучей. Для устранения сомнений Томсон создавал перед фотопластинкой магнитное поле. В результате картина, создаваемая электронами, смазывалась. Итак, опыты Томсона показали, что при рассеянии электронов на тонкой металлической фольге они (электроны) проявляют волновые свойства с длиной волны Де Бройля. 4. Дифракция отдельных электронов.Опыты Дэвиссона-Джермера и Томсона подтвердили формулу дебройлевской длины волны (3.1). Однако эти опыты были выполнены с электронными пучками больших интенсивностей, в которых концентрация электронов была настолько велика, что их нельзя было считать системой невзаимодействующих частиц. Поэтому оставалось допущение, что дифракция электронного пучка есть свойство коллектива электронов, а не отдельных электронов. Чтобы снять сомнения, Л. Биберман, Н. Сушкин и В. Фабрикант в 1949 г. поставили опыт с электронными пучками столь малых интенсивностей, что электроны проходили через мишень заведомо поодиночке. Паузы были в 30000 раз продолжительнее времени прохождения электрона. Результаты опытов вновь подтвердили формулу Де Бройля. 5.Соотношение неопределённостей Гейзенберга. Из анализа накопленного к концу двадцатых годов экспериментального материала следовало, что есть явления, в которых электроны ведут себя как частицы. Это, например, движение электронов в катодных лучах, в электронно-лучевых трубках, в камере Вильсона. Здесь их движение может быть описано в понятиях классической механики, а сами электроны могут моделироваться материальными точками. Но есть такие явления, в которых положение электронов в пространстве определяются вероятностными законами. Это, например, рассеяние электронов на кристаллах. Здесь нельзя говорить о траекториях их движения, поскольку исчезает механическая однозначность в поведении микрообъектов. Если рассмотреть дифракционные кольца на фотопластинках в опытах Томсона под микроскопом, то все эти кольца распадаются на кольцевые системы точечных почернений. Отдельный электрон никаких дифракционных колец не дает, он поглощается как частица. Дифракционные кольца образуются разной густотой электронных следов. В местах дифракционных максимумов густота больше, в местах минимумов – меньше. В какую точку попадёт электрон, сказать однозначно нельзя. На вопрос: каковы критерии применимости классической или квантовой модели – ответил в 1927 г. немец Вернер Гейзенберг. Он открыл соотношение неопределённостей для координаты и импульса микрочастиц. Он рассуждал примерно так. Чтобы определить поглощение и импульс электрона, нужно осветить его и получить хотя бы один рассеянный при столкновении фотон. Вследствие дифракции погрешность определения координаты электрона не может быть меньше длины волны фотона, ∆x ≈ λ. Чем точнее нужно определить положение электрона, тем меньше должно быть λ, тем более жёстким будет фотон. При столкновении с фотоном электрон получает отдачу, которая тем больше, чем больше импульс фотона h/λ. Итак, уменьшая погрешность в координате ∆x, мы увеличиваем погрешность в импульсе ∆рx, и наоборот.
Соотношение неопределённостей для координат – импульса. Гейзенберг, 1927г.
Здесь ∆р и ∆х, ∆y, ∆z – среднеквадратичные отклонения этих величин от их средних значений. Из соотношения неопределённостей следует, что чем точнее определена одна из входящих в неравенство величин, тем менее определённым становится значение другой. Никакой эксперимент не может дать одновременно точные значения координаты и импульса микрочастицы. Дальнейшее развитие квантовой механики показало, что суть соотношения неопределённостей не в том, что несовершенны измерительные системы. Суть в том, что неопределённость координаты и импульса есть объективное свойство материи. Соотношение неопределённостей можно записать еще для двух величин – энергии Е и времени t.
Произведение энергии на время называют действием. Поэтому выражение ∆E∆t называют неопределённостью действия. Соотношение неопределённостей (3.8) выражает принцип соответствия. Если Если система находится в стационарном состоянии, то есть в состоянии, которое при отсутствии внешних сил не меняется, то энергию системы в этом состоянии можно измерить лишь с погрешностью не менее h/∆t, где ∆t – длительность процесса измерения. Если же система нестационарна, то неопределённость значения энергии не может быть меньше h/∆t, где ∆t – характерное время, в течение которого существенно меняются средние значения физических параметров этой системы. 6. Микрочастицы и принцип наглядности. С развитием квантовой физики пришлось отказаться от наглядности физических моделей. Рассмотрим мысленный эксперимент по дифракции электронов на двух отверстиях. Мысленный потому, что диаметр отверстий должен быть одного порядка с диаметром атома водорода, что технически трудно сделать. Однако дифракция электронов на атомных плоскостях показывает, что события должны развиваться именно так.
Рассмотрим дифракцию электронов по схеме Юнга. На пути электронного пучка находится экран Э1 с двумя отверстиями 1 и 2. Далее по ходу движения электронов находится экран Э2 с фотопластинкой ФП (рис. 14, вверху). Мысленно представим, что электроны поодиночке проходят через 1-е отверстие Если же открыть оба отверстия, то получится не сумма дифракционных картин отдельных отверстий, а дифракционная картина на двух отверстиях сразу (рис. 14, внизу справа). Получается, что каждый электрон проходит одновременно через оба отверстия. В то же время во всех явлениях электрон – целостный не дробящийся объект. Ситуация ненаглядна. Но это объективное свойство квантовых моделей.
Уравнение Шрёдингера 1. Уравнение Шрёдингера. В 1925 г. австрийский физик Эрван Шрёдингер, основываясь на общих соображениях, сконструировал дифференциальное уравнение для волновой функции Де Бройля Здесь Для систем в стационарном состоянии. Здесь E – полная энергия системы. В случае стационарного поля она остаётся постоянной. Уравнение Шрёдингера является основным уравнением нерелятивистской квантовой механики. Его справедливость доказывается тем, что все вытекающие из него следствия очень хорошо согласуются с ответом. Поэтому до настоящего времени уравнение Шрёдингера вызывает у некоторых физиков чувство полумистического восхищения. 2. Вероятностный смысл функции Ψ. В том же 1926 г. немец Макс Борн показал, что функция Ψ имеет вероятностный смысл. Квадрат модуля волновой функции
Из вероятностного смысла волновой функции Ψ следует, что квантовая механика имеет статистический характер. Она не позволяет определить положение частицы в пространстве или определить траекторию её движения. В рамках квантовой механики ставить вопрос о точном местонахождении частицы или о траектории её движения некорректно. С помощью волновой функции Ψ можно лишь предсказать, с какой вероятностью частица может быть обнаружена в разных по величине и положению объёмах пространства. 3.Частица в одномерной потенциальной яме. Математический аппарат квантовой механики очень труден. Число задач, в которых уравнение Шрёдингера решается точно, невелико. Самая простая задача о движении частицы в одномерной потенциальной яме рассматривается здесь для того, чтобы познакомиться с некоторыми понятиями квантовой механики и убедиться в том, что условия квантования энергии заложены в самом уравнении Шрёдингера. Рассмотрим состояние частицы в одномерной бесконечно глубокой прямоугольной потенциальной яме. Это значит, что потенциальная энергия U частицы удовлетворяет условиям:
Здесь l – длина потенциальной ямы вдоль оси ОX. Так как в задаче нет изменяющихся во времени силовых полей, то она соответствует уравнению Шрёдингера для стационарных состояний (4.2). В декартовых координатах, в которых составлена задача, выражение ∆Ψ имеет вид:
Задача одномерная, члены, содержащие переменные y и z, выпадают. Уравнение (4.2) упрощается. (Напомним, что в яме U = 0).
Покажем, что стенки ямы непроницаемы для частицы. Выйти за пределы ямы она не может. Отсюда следуют граничные условия для волновой функции Ψ.
Обозначим коэффициент
Это уравнение напоминает уравнение движения незатухающего гармонического осциллятора. Разница в том, что в осцилляторе независимая переменная – время t. Здесь независимая переменная – координата x. Решение уравнения (4.8) имеет вид:
4. Квантование энергии. Найдём по условиям задачи постоянные интегрирования А и α. Воспользуемся вначале краевыми условиями (4.7).
Из первого условия вытекает Из второго условия также нельзя определить амплитуду А. Но из него вытекает условие квантовой энергии частицы. Действительно,
Условие n = 0 нужно исключить, так как здесь получается Итак, из условия (4.11) следует:
В уравнении Шрёдингера уже заложен дискретный спектр значений энергии частицы Е. Уравнение Шрёдингера (4.8) имеет решение не при любых значениях Е, а лишь при некоторых, определяемых формулой (4.12). Эти избранные значения Е называются собственными значениями параметра, в данном случае, собственными значениями энергии Е. 5. Нормировка волновой функции. Вторая постоянная интегрирования – амплитуда А функции Ψнаходится из условия нормировки. Суть этого условия в том, что достоверно известно, что частица находится в яме. Вероятность P пребывания частицы в яме равна 1.
Так как
Итак, Решение уравнения (4.8) имеет вид:
Значения Ψ, удовлетворяющие уравнению Шрёдингера, называются собственными функциями уравнения Шрёдингера.
На рис. 16а слева показан график функции Ψ в яме при разных квантовых числах n = 1, 2, 3, … То, что значения Ψ в каждой точке пространства не меняется во времени (стационарная задача) позволяет толковать её как стоячую волну, образованную сложением бегущей волны (слева направо) с упруго отражённой от стенки x = l (справа налево). При n = 1 наиболее вероятное пребывание частицы в области середины ямы x = l/2. При n = 2 обнаружить частицу в центре маловероятно. Зато с одинаковой вероятностью можно найти её вблизи центров x = l/4 и x =3l/4 «половинок» ямы. Длина волны λ, характеризующая волну Ψ, найдётся из уравнения: 7. Ротатор. Квантование момента импульса. Ротатором в квантовой механике называется неизменная вращающаяся система, состоящая из частицы массой m c угловой степенью свободы. То есть полагается, что частица может двигаться по окружности радиуса r со скоростью v. Координатой движения является угол поворота φ. Поскольку система квантовая, то по окружности движения частицы должна распространятся волна Де Бройля. Решение уравнения Шрёдингера для обоснований условий квантования момента импульса ротатора является сложной математической задачей. В отличие от классической механики в квантовой механике определённые значения одновременно могут иметь только квадрат момента импульса L2 и одна из проекций момента импульса на координатную ось, например Lz. а. Квадрат момента импульса L2 принимает дискретный ряд значений,
так называемое азимутальное квантовое число. В зависимости от энергетического уровня число l может принимать значения от 0 до п – 1, где п – главное квантовое число. б. Проекция момента импульса на произвольную ось Z также принимает дискретный ряд значений,
так называемое магнитное квантовое число. в.Проекция момента импульса на произвольную ось Z не может превосходить его модуля Отсюда следует, что максимально возможное значение числа Заметим, что произвольная ось Z задаётся в эксперименте обычно с помощью электрического или магнитного поля. В этом случае в качестве оси Z берут направление силовых линий поля. Неопределённость ориентации момента импульса L квантовой системы не есть лишь свидетельство размытости момента импульса в пустом пространстве. Оно остаётся неопределённым и при наличии внешнего воздействия со стороны поля. Квантовое число m определяет ориентацию момента импульса L относительно
Модуль момента импульса |



 . Формула Бальмера, 1885
. Формула Бальмера, 1885 . Серия Лаймана, 1906
. Серия Лаймана, 1906 Обобщённая формула Бальмера
Обобщённая формула Бальмера
 – заряд шаровой области радиуса r £ R,
– заряд шаровой области радиуса r £ R,  .
. , а me – масса электрона.
, а me – масса электрона. . Ускоренно движущийся электрон излучает электромагнитную волну той же частоты ω0.
. Ускоренно движущийся электрон излучает электромагнитную волну той же частоты ω0. , (1.8)
, (1.8) . (1.9)
. (1.9) (1.17)
(1.17) м/с. В ядерной модели Резерфорда внутренняя структура атома приобретала знакомые из небесной механики очертания. Вокруг ядра как вокруг Солнца движутся электроны – планеты. С точки зрения механики система устойчива.
м/с. В ядерной модели Резерфорда внутренняя структура атома приобретала знакомые из небесной механики очертания. Вокруг ядра как вокруг Солнца движутся электроны – планеты. С точки зрения механики система устойчива. (1.18)
(1.18) м/с2. По меркам микрофизики это гигантская величина. Электрический заряд, испытывающий ускорение, по законам классической электродинамики излучает электромагнитную волну. Энергия ЭМ волны может черпаться лишь из энергии электрона. Но это значит, что радиус орбиты электрона должен постепенно уменьшаться.
м/с2. По меркам микрофизики это гигантская величина. Электрический заряд, испытывающий ускорение, по законам классической электродинамики излучает электромагнитную волну. Энергия ЭМ волны может черпаться лишь из энергии электрона. Но это значит, что радиус орбиты электрона должен постепенно уменьшаться. с. Спустя это время электрон должен упасть на ядро, а атом должен превратиться в какой-то другой объект материи.
с. Спустя это время электрон должен упасть на ядро, а атом должен превратиться в какой-то другой объект материи. Правило квантования орбит
Правило квантования орбит Правило частот Бора
Правило частот Бора
 В.
В.
 Дж. Разделив это число на заряд электрона
Дж. Разделив это число на заряд электрона 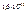 Кл, получаем энергию фотона в электронвольтах,
Кл, получаем энергию фотона в электронвольтах,  эВ. Это как раз энергия электронов eΔU1 при резонансном поглощении.
эВ. Это как раз энергия электронов eΔU1 при резонансном поглощении. или
или  (2.4)
(2.4)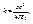 k – радиус орбиты электрона, me – масса покоя электрона.
k – радиус орбиты электрона, me – масса покоя электрона. (2.5)
(2.5)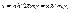 где
где  Подставляем в первое уравнение.
Подставляем в первое уравнение. (2.7)
(2.7) м.
м. м.
м. ),
),  Один ангстрём равен приблизительно поперечнику атома водорода в основном состоянии.
Один ангстрём равен приблизительно поперечнику атома водорода в основном состоянии. (2.8)
(2.8) (2.9)
(2.9) м/с, что совпадает со значением, вычисленном на с.
м/с, что совпадает со значением, вычисленном на с. м/с, на третьем, n = 3, скорость в 3 раза меньше и т.д.
м/с, на третьем, n = 3, скорость в 3 раза меньше и т.д. (2.10)
(2.10)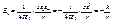 (2.11)
(2.11) где e– – заряд электрона, отрицательное число.
где e– – заряд электрона, отрицательное число. (2.12)
(2.12) (2.13)
(2.13)
 из области отрицательных значений.
из области отрицательных значений. называют возбуждёнными.
называют возбуждёнными.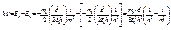
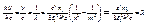 (2.15
(2.15 м–1.
м–1. м–1.
м–1. (2.16)
(2.16)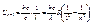
 При n = 3 получаем 2-й потенциал возбуждения атома водорода U2 = 12,12 В. Подставляя n = 4, 5, 6, и т.д., можно вычислить все последующие потенциалы возбуждения U3 = 12,79 В, U4 = 13,09 В…
При n = 3 получаем 2-й потенциал возбуждения атома водорода U2 = 12,12 В. Подставляя n = 4, 5, 6, и т.д., можно вычислить все последующие потенциалы возбуждения U3 = 12,79 В, U4 = 13,09 В… электрон в атоме обладает орбитальным магнитным моментом.
электрон в атоме обладает орбитальным магнитным моментом. (2.18)
(2.18) Дж/ТЕго называют магнетон Бора.
Дж/ТЕго называют магнетон Бора. где m = 5, 6, 7, … Серия Пикеринга
где m = 5, 6, 7, … Серия Пикеринга . Физический смысл величины Е зависит от того, в какой модели рассматривается свет. В 1924 г. француз Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм (двойственность) присущ не только микрообъектам полевой формы материи (фотонам), но и микрообъектам, которые традиционно понимались до этого как частицы (масса покоя не равна нулю). То есть к электронам, ядрам, атомам. Иначе, дуализм есть универсальное свойство материи.
. Физический смысл величины Е зависит от того, в какой модели рассматривается свет. В 1924 г. француз Луи де Бройль выдвинул гипотезу, что корпускулярно-волновой дуализм (двойственность) присущ не только микрообъектам полевой формы материи (фотонам), но и микрообъектам, которые традиционно понимались до этого как частицы (масса покоя не равна нулю). То есть к электронам, ядрам, атомам. Иначе, дуализм есть универсальное свойство материи. движения частицы. Хотя физический смысл функции ψ оставался ещё неясным.
движения частицы. Хотя физический смысл функции ψ оставался ещё неясным. . Отсюда, длина волны фотона с импульсом p есть
. Отсюда, длина волны фотона с импульсом p есть  . Применительно к частице её импульс p = mv. Отсюда
. Применительно к частице её импульс p = mv. Отсюда Длина волны Де Бройля (3.1)
Длина волны Де Бройля (3.1) где n = 1, 2, 3, ... (3.2)
где n = 1, 2, 3, ... (3.2)
 (3.3)
(3.3) .
. (рис. 11).В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния θ (0<θ<90°), от азимутального угла φ (0≤φ≤360°), от скорости v электронов в пучке.
(рис. 11).В опытах измерялась интенсивность рассеянного кристаллом электронного пучка в зависимости от угла рассеяния θ (0<θ<90°), от азимутального угла φ (0≤φ≤360°), от скорости v электронов в пучке.
 . При изменении азимутального угла φ максимумы повторялись через 120°.
. При изменении азимутального угла φ максимумы повторялись через 120°. при k = 1
при k = 1 

 (3.4)
(3.4)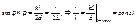 (3.5)
(3.5) (3.6) Здесь β = v/с,
(3.6) Здесь β = v/с,  – масса покоя электрона.
– масса покоя электрона. , что около половины скорости света с.
, что около половины скорости света с. нужно подставлять релятивистскую массу электрона
нужно подставлять релятивистскую массу электрона  В нашем примере длина
В нашем примере длина 
 Обычно соотношение неопределённостей записывают для проекций импульса и координат.
Обычно соотношение неопределённостей записывают для проекций импульса и координат. . Принцип соответствия (3.8)
. Принцип соответствия (3.8) , явление описывается классическими законами, при
, явление описывается классическими законами, при  – квантовыми.
– квантовыми. . Общее уравнение Шрёдингера
. Общее уравнение Шрёдингера – мнимая единица, ħ=h/2π, m – масса частицы, U – потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа.
– мнимая единица, ħ=h/2π, m – масса частицы, U – потенциальная энергия частицы, функция координат, t – время, ∆ – оператор Лапласа. . Уравнение Шрёдингера для стационарных состояний
. Уравнение Шрёдингера для стационарных состояний определяет плотность вероятности p нахождения частицы в точке пространства,
определяет плотность вероятности p нахождения частицы в точке пространства,  . Вероятность P нахождения частицы в объёме пространства V находится интегрированием.
. Вероятность P нахождения частицы в объёме пространства V находится интегрированием. (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) или
или  (4.6)
(4.6)
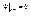 (4.7)
(4.7) Тогда
Тогда (4.8)
(4.8)

 (4.10)
(4.10) (Случай А = 0 приводит к тому, что
(Случай А = 0 приводит к тому, что  в любой точке ямы. Но это возможно лишь при отсутствии там частицы, что противоречит условию задачи).
в любой точке ямы. Но это возможно лишь при отсутствии там частицы, что противоречит условию задачи).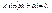 При
При 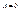 и
и  отсюда следует:
отсюда следует: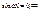
 где n = 1, 2, 3, ... (4.11)
где n = 1, 2, 3, ... (4.11) А это значит Ψ = 0 при любых x.
А это значит Ψ = 0 при любых x.
 (4.12)
(4.12) (4.13)
(4.13) то
то


 (4.15)
(4.15)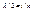
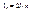
 где l = 0, 1, 2, … (4.22)
где l = 0, 1, 2, … (4.22) где m = 0, ±1, ±2, … (4.23)
где m = 0, ±1, ±2, … (4.23)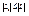 или
или  (4.24)
(4.24) как целого числа равно l. Даже при m = l
как целого числа равно l. Даже при m = l  Это обусловлено тем, что направление момента импульса в пространстве является неопределённым.
Это обусловлено тем, что направление момента импульса в пространстве является неопределённым. Это радиус сферы, в которой вписаны три конуса с вершинами в центре сферы. При m = 0 конус вырождается в диск, Lz = 0. При m=+1 получаем конус в верхней части, его высота Lz равна +ћ. При m = –1 получаем конус в нижней части, его высота Lz = –ћ. То, что известна одна проекция на ось, можно толковать так, что вектор
Это радиус сферы, в которой вписаны три конуса с вершинами в центре сферы. При m = 0 конус вырождается в диск, Lz = 0. При m=+1 получаем конус в верхней части, его высота Lz равна +ћ. При m = –1 получаем конус в нижней части, его высота Lz = –ћ. То, что известна одна проекция на ось, можно толковать так, что вектор