 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Доходность и риск портфеля ценных бумаг
В теории портфельного инвестирования исходят из того, что значения доходности отдельной ценной бумаги портфеля являются случайными величинами, распределенными по нормальному (Гауссовскому) закону. Чтобы определить распределение вероятностей случайной величины Субъективный подход имеет важное преимущество, поскольку позволяет оценивать сразу будущиезначение доходности. Однако, он не находит широкого применения, поскольку для обычного инвестора очень трудно сделать оценку вероятностей экономических сценариев и ожидаемую при этом доходность. Чаще используется объективный,или историческийподход. В его основе лежит предположение о том, что распределение вероятностей будущих (ожидаемых) величин практически совпадает с распределением вероятностей уже наблюдавшихсяфактических, исторических величин. Значит, чтобы получить представление о распределении случайной величины Как показывают исследования западных экономистов, для рынка акций наиболее приемлемым является промежуток 7-10 шагов расчета. В отличие от субъективного подхода, который предполагает разную вероятность различных значений доходности, при Наиболее часто в теории инвестиционного портфеля используется среднее арифметическоезначение случайных величин. Напомним, что если
где N – количество лет, в течение которых велись наблюдения. В случае объективного подхода
Наиболее часто риск ценной бумаги измеряют с помощью дисперсии
Доходность портфеля.Подожидаемой доходностьюпортфеля понимается средневзвешенное значение ожидаемых значений доходности ценных бумаг, входящих в портфель. При этом "вес" каждой ценной бумаги определяется относительным количеством денег, направленных инвестором на покупку этой ценной бумаги. Ожидаемая доходность инвестиционного портфеля равна:
где
n – число ценных бумаг в портфеле. Измерение риска портфеля.При определении риска портфеля следует учитывать, что дисперсию портфеля нельзянайти как средневзвешенную величин дисперсий входящих в портфель ценных бумаг. Это объясняется тем, что дисперсия портфеля зависит не только от дисперсий входящих в портфель ценных бумаг, но также и от взаимосвязи доходностей ценных бумаг портфеля друг с другом. Иными словами, риск портфеля объясняется не только индивидуальным риском каждой отдельно взятой ценной бумаги портфеля, но и тем, что существует риск воздействия изменений наблюдаемых ежегодных величин доходности одной акции на изменения доходности других акций, включаемых в инвестиционный портфель. Меру взаимозависимости двух случайных величин измеряют с помощью ковариации и коэффициента корреляции. Положительная ковариацияозначает, что в движении доходности двух ценных бумаг имеется тенденция изменяться в одних и тех же направлениях: если доходность одной акции возрастает (уменьшается), то и доходность другой акции также возрастет (уменьшится). Если же просматривается обратная тенденция, то есть увеличению (уменьшению) доходности акций одной компании соответствует снижение (увеличение) доходности акций другой компании, то считается, что между доходностями акций этих двух компаний существует отрицательная ковариация. Когда рассматриваются величины доходности ценных бумаг за прошедшие периоды, то ковариация подсчитывается по формуле:
где
N – общее количество лет наблюдения. Часто при определении степени взаимосвязи двух случайных величин используют относительнуювеличину – коэффициент корреляции
Итак, риск инвестиционного портфеля надо определять с помощью дисперсии. Пусть в исследуемый портфель входят n ценных бумаг; тогда дисперсию портфеля необходимо вычислять по формуле:
Учитывая, что коэффициент корреляции
2 тема Основные положения модели Г. Марковица
Знание ожидаемой доходности активов, а также уровня риска ее получения используется при формировании инвесторами так называемых оптимальных портфелей ценных бумаг. Оптимизация портфелей ценных бумаг состоит в определении пропорций в составе входящих в него активов, которые бы обеспечили максимальную доходность при минимуме риска. Решение проблемы оптимального распределения долей капитала между ценными бумагами, сводящего общий риск к минимальному уровню, и составление оптимального портфеля было предложено в 50-е годы XX века американским ученым Г. Марковицем. Формализованная модель Г. Марковица, а также разработанная в начале 60-х годов модель В Шарпа, позволяет добиваться формирования такого инвестиционного портфеля, который бы отвечал потребностям и целям каждого индивидуального инвестора. Как любая формализованная модель, указанные модели имеют ряд допущений и могут быть реализованы только при определенных условиях (на отечественном фондовом рынке не все есть условия). В 1952 г. американский экономист Г. Марковиц опубликовал статью "Рогtfolio Selection", которая легла в основу теории инвестиционного портфеля. Г. Марковиц исходил из предположения о том, что инвестирование рассматривается как однопериодовый процесс, т.е. полученный в результате инвестирования доход не реинвестируется. Другим важным исходным положением в теории Г. Марковица является идея об эффективности рынка ценных бумаг. Под эффективнымрынком понимается такой рынок, на котором вся имеющаяся информация трансформируется в изменение котировок ценных бумаг; это рынок, который практически мгновенно реагирует на появление новой информации. В своих теоретических исследованиях Марковиц полагал, что значения доходности ценных бумаг являются случайными величинами, распределенными по нормальному (Гауссовскому) закону. В этой связи Марковиц считал, что инвестор формируя свой портфель, оценивает лишь два показателя Ключ к решению проблемы выбора оптимального портфеля лежит в теореме о существовании эффективного набора портфелей,так называемой границы эффективности.Суть теоремы сводится к выводу о том, что любой инвестор должен выбрать из всего бесконечного набора портфелей такой портфель, который: 1. Обеспечивает максимальную ожидаемую доходность при каждом уровне риска. 2. Обеспечивает минимальный риск для каждой величины, ожидаемой доходности. Набор портфелей, которые минимизируют уровень риска при каждой величине ожидаемой доходности, образуют так называемую границу эффективности. Эффективный портфель – это портфель, который обеспечивает минимальный риск при заданной величине Та часть риска портфеля, которая может быть устранена путем диверсификации, называется диверсифицируемым,или несистематическимриском. Доля же риска, которая не устранятся диверсификацией, носит название недиверсифицируемого,или систематическогориска. Если портфель состоит из более чем из 2 ценных бумаг, то для любого заданного уровня доходности существует бесконечное число портфелей, или, иными словами, можно сформулировать бесконечное количество портфелей, имеющих одну и ту же доходность. Тогда задача инвестора сводится к следующему: из всего бесконечного набора портфелей с ожидаемой доходностью необходимо найти минимальное значение дисперсии портфеля
при заданных начальных условиях:
Для решения задачи нахождения оптимального портфеля, содержащего n ценных бумаг, необходимо первоначально вычислить: 1. n значений ожидаемой доходности 2. n значений дисперсий 3. n(n-1)/2 значений ковариации Если подставить значения В теории Марковица инвесторы стремятся сформировать портфель ценных бумаг, чтобы максимизировать получаемую полезность. Иными словами, каждый инвестор желает таким образом сформировать портфель, чтобы сочетание ожидаемой доходности На практике конкретный инвестор, построив границу эффективных портфелей, должен задать себе вопрос – какую доходность он ожидает от портфеля? После этого по кривой границы эффективных он определяет уровень
6 тема Оптимизация инвестиционного портфеля по методу У. Шарпа
В 1963 г. американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель Шарпа (Sharpe single-index model). В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две переменные величины - независимую X и зависимую Y линейным выражением типа Пусть норма отдачи
где:
Особое значение необходимо уделить параметру В общем случае, если Как показывают исследования, для большинства ценных бумаг Ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле:
где
Для придания этой формуле компактности, Шарп предложил считать рыночный индекс как характеристику условной (n+1)-ой ценной бумаги в портфеле. В таком случае, второе слагаемое уравнения (56) можно представить в виде:
где:
при этом считается, что дисперсия (n+1)-ой ошибки равна дисперсии рыночной доходности:
а поскольку
Итак, ожидаемую доходность портфеля а) суммы взвешенных параметров б) компоненты Дисперсия портфеля в модели Шарпа представляется в виде:
При этом необходимо иметь в виду, что а) средневзвешенных дисперсий ошибок б) В модели Шарпа цель инвестора сводится к следующему: необходимо найти минимальное значение дисперсии портфеля
при следующих начальных условиях:
Таким образом для построения границы эффективных портфелей в модели Шарпа необходимо выполнить следующие основные этапы: 1. Выбрать n ценных бумаг, из которых формируется портфель, и определить 2. По рыночному индексу (например, АК&М) вычислить рыночные доходности 3. Определить величину дисперсии рыночного показателя
4. Найти ожидаемые доходности каждой ценной бумаги
5. Вычислить дисперсии 6. Подставить эти значения в соответствующие уравнения После такой подстановки выяснится, что неизвестными величинами являются веса
|




 необходимо знать, какие фактические значения
необходимо знать, какие фактические значения  принимает данная величина, и какова вероятность
принимает данная величина, и какова вероятность  каждого подобного результата. При этом инвестора интересует доходность инвестиций в конце инвестиционного, холдингового периода, то есть будущиезначения
каждого подобного результата. При этом инвестора интересует доходность инвестиций в конце инвестиционного, холдингового периода, то есть будущиезначения  При использовании субъективного подхода инвестор, прежде всего, должен определить возможные сценарии развития экономической ситуации в течение холдингового периода, оценить вероятность каждого результата и ожидаемую при этом доходность ценной бумаги.
При использовании субъективного подхода инвестор, прежде всего, должен определить возможные сценарии развития экономической ситуации в течение холдингового периода, оценить вероятность каждого результата и ожидаемую при этом доходность ценной бумаги. наблюдениях случайной величины вероятность конкретного результата составляет величину
наблюдениях случайной величины вероятность конкретного результата составляет величину  . Например, если исследуется доходность акции за предшествующие 10 лет, то вероятность каждой годовой доходности
. Например, если исследуется доходность акции за предшествующие 10 лет, то вероятность каждой годовой доходности  ,(t = 1,2,….,N) представляют собой значения доходности в конце t –го периода, а
,(t = 1,2,….,N) представляют собой значения доходности в конце t –го периода, а  - вероятности данных значений доходности, то:
- вероятности данных значений доходности, то:
 – среднее арифметическое значение доходности;
– среднее арифметическое значение доходности; (43)
(43) и стандартного отклонения
и стандартного отклонения  .
. (44)
(44) (45)
(45)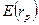 – ожидаемая норма отдачи портфеля;
– ожидаемая норма отдачи портфеля; – доля в общих инвестиционных расходах, идущая на приобретение i-той ценной бумаги (“вес” i-той ценной бумаги в портфеле);
– доля в общих инвестиционных расходах, идущая на приобретение i-той ценной бумаги (“вес” i-той ценной бумаги в портфеле); – ожидаемая доходность i-той ценной бумаги;
– ожидаемая доходность i-той ценной бумаги; (46)
(46) – ковариация между величинами доходности ценной бумаги i и ценной бумаги j;
– ковариация между величинами доходности ценной бумаги i и ценной бумаги j;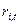 и
и  – доходность ценных бумаг i и j в момент времени t ;
– доходность ценных бумаг i и j в момент времени t ; и
и  – ожидаемая (среднеарифметическая) доходность ценных бумаг i и j;
– ожидаемая (среднеарифметическая) доходность ценных бумаг i и j; :
: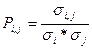 (47)
(47) (48)
(48) , то эту формулу можно представить в виде:
, то эту формулу можно представить в виде: (49)
(49) – ожидаемую доходность и
– ожидаемую доходность и  необходимо найти такой, который обеспечивал бы минимальный уровень риска. Иными словами, можно задачу инвестора свести к следующему:
необходимо найти такой, который обеспечивал бы минимальный уровень риска. Иными словами, можно задачу инвестора свести к следующему: (52)
(52) (53)
(53) каждой ценной бумаги;
каждой ценной бумаги; , где i,j=1,2,….,n
, где i,j=1,2,….,n и
и  инвестор должен найти такие значения
инвестор должен найти такие значения  модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал норму отдачи
модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал норму отдачи  , вычисленную на основе индекса Standart and Poors (S&P500). В качестве зависимой переменной берется отдача
, вычисленную на основе индекса Standart and Poors (S&P500). В качестве зависимой переменной берется отдача  ,
,  ,…,
,…,  . При этом доходность
. При этом доходность  ,
,  ,…,
,…,  . В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами
. В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами 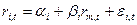 (54)
(54) – параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг
– параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг  – параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности;
– параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности; – доходность рыночного портфеля в момент t;
– доходность рыночного портфеля в момент t; – случайная ошибка, свидетельствующая о том, что реальные, действующие значения
– случайная ошибка, свидетельствующая о том, что реальные, действующие значения  < 1 ценная бумага имеет меньший размах отклонений доходности
< 1 ценная бумага имеет меньший размах отклонений доходности  , от средней арифметической (ожидаемой) величины
, от средней арифметической (ожидаемой) величины  , чем рыночная норма отдачи. В этой связи ценные бумаги с коэффициентом
, чем рыночная норма отдачи. В этой связи ценные бумаги с коэффициентом  > 1 классифицируются как более рискованные, чем рынок в целом, а с
> 1 классифицируются как более рискованные, чем рынок в целом, а с  (55)
(55) (56)
(56) (57)
(57) ; (57а)
; (57а) .
. . Выражение (15а) представляет собойсумму взвешенных величин "беты" (
. Выражение (15а) представляет собойсумму взвешенных величин "беты" (  ). С учетом выражений (56) и (57) формулу (55) можно записать так:
). С учетом выражений (56) и (57) формулу (55) можно записать так: (58)
(58) , то окончательно имеем:
, то окончательно имеем: (59)
(59) …..+
…..+  , что отражает вклад в
, что отражает вклад в  , то есть произведенияпортфельной бетыи ожидаемой рыночной доходности, что отражает взаимосвязь рынкас ценными бумагами портфеля.
, то есть произведенияпортфельной бетыи ожидаемой рыночной доходности, что отражает взаимосвязь рынкас ценными бумагами портфеля. (60)
(60) , то есть
, то есть 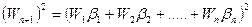 , а
, а 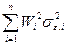 , где весами служат
, где весами служат 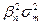 - взвешенной величины дисперсии рыночного показателя
- взвешенной величины дисперсии рыночного показателя  , где весом служит квадрат портфельной беты,что отражает долюриска портфеля, определяемого нестабильностью самого рынка (рыночныйриск)
, где весом служит квадрат портфельной беты,что отражает долюриска портфеля, определяемого нестабильностью самого рынка (рыночныйриск) (62)
(62) (64)
(64) доходностей каждой ценной бумаги с рыночной
доходностей каждой ценной бумаги с рыночной
 и вычислить параметр
и вычислить параметр  :
:
 ошибок регрессионной модели
ошибок регрессионной модели