 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Третий способ – сокращенный.
Практическое занятие № 4 «Логические рассуждения» Определение: Пусть даны две формулы Для логического следования используется запись: Три способа проверки правильности логического рассуждения: I. Применить определение: а) записать все посылки и заключения в виде формул логики высказываний; б) составить конъюнкцию формализованных посылок в) проверить по таблице истинности, следует ли заключение II. Использовать Признак логического следования: Формула III. Применить сокращенный способ проверки правильности логического рассуждения. Рассуждение строится «методом от противного»: Рассуждение является неправильным, если найдется набор значений переменных Сокращенный метод заключается в следующем. Пусть требуется проверить правильность логического следования формулы Предположим, что существует набор Если в параллелограмме диагонали взаимно перпендикулярны (А), то параллелограмм – ромб (B). В данном параллелограмме диагонали не взаимно перпендикулярны (отрицание А), следовательно, он не является ромбом (отрицание B)». Решение: Составим схему логического рассуждения:
Первый способ проверки – по определению.Составляем конъюнкцию формализованных посылок: Проверим по таблице истинности:
Так как на наборе (A=0, B=1) конъюнкция посылок истинна, а заключение ложно, то рассуждение не является логически правильным. Второй способ, основанный на признаке логического следования. Построим формулу
Расставим приоритеты логических операций и построим таблицу истинности.
Формула Третий способ – сокращенный. Проверим сокращенным способом правильность логического рассуждения Пусть существует набор
Из строк 2,3 следует: Если число представлено в виде несократимой дроби (A), то оно рациональное (B). Если число целое (C), то оно не является рациональным(отриц. В). Следовательно, если число целое(С), то оно не представлено в виде несократимой дроби(отриц. А)». Решение: Составим схему логического рассуждения:
Первый способ проверки – по определению.Составляем конъюнкцию формализованных посылок: Проверим по таблице истинности:
Так как нет наборов, где конъюнкция посылок истинна, а заключение ложно, то данное рассуждение является логически правильным. Второй способ, основанный на признаке логического следования. Построим формулу
Расставим приоритеты логических операций и построим таблицу истинности.
Формула |



 . Формула
. Формула  является логическим следованием формул
является логическим следованием формул 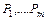 , если, придавая значения переменным
, если, придавая значения переменным 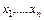 , от которых зависят все рассматриваемые формулы, всякий раз, когда истинны одновременно все формулы
, от которых зависят все рассматриваемые формулы, всякий раз, когда истинны одновременно все формулы 
 ;
; тогда и только тогда, когда формула
тогда и только тогда, когда формула  является тавтологией. Для проверки необходимо построить таблицу истинности для формулы
является тавтологией. Для проверки необходимо построить таблицу истинности для формулы  такой, что посылка
такой, что посылка  , при котором все посылки истинны, а заключение ложно, и попытаемся найти этот набор. Если такой набор будет обнаружен, то наше предположение оправдалось, и рассуждение является логически неправильным. Если в процессе поисков набора придем к противоречию, то наше предположение ошибочно, а рассуждение является логически правильным.
, при котором все посылки истинны, а заключение ложно, и попытаемся найти этот набор. Если такой набор будет обнаружен, то наше предположение оправдалось, и рассуждение является логически неправильным. Если в процессе поисков набора придем к противоречию, то наше предположение ошибочно, а рассуждение является логически правильным.

 .
.





 .
.






 ├─
├─  .
.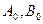 при котором посылки истинны, а заключение ложно. Оформим это предположение в виде таблицы
при котором посылки истинны, а заключение ложно. Оформим это предположение в виде таблицы

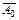




 .
.



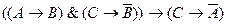 .
.