 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Психологические закономерности формирования математических понятий
Формирование математических понятий Пропедевтика понятий Пропедевтика (гр. propaideuo- обучаю предварительно) – введение в какую-либо науку. Следовательно, речь идет о предварительной подготовке учащихся к формированию математических понятий. Математические понятия – важнейшая неотъемлемая часть науки и учебного предмета математики. Каждая математическая наука и учебная дисциплина начинается с первичных, основных неопределяемых понятий. Все другие определяются и называются определяемыми, выводными или производными. Это можно сделать в систематических курсах математических дисциплин, т.е. на определенном уровне развития учащихся. На начальной ступени обучения учащиеся знакомятся с большинством математических понятий наглядно, путем созерцания конкретных примеров или практического оперирования ими, например, при счете их. При этом учитель опирается на жизненный опыт учащихся. Способы введения мат. понятий на начальном этапе изучения математики: 1) первое знакомство с математическими понятиями в начальных классах школы фиксируется с помощью термина и символа, без описания или определения понятия. Например, фигуры треугольник, квадрат, прямоугольник - еще в детском саду. Термин «меньше» и символ 2< 9; термин «сложение» и символ «+» и т.д.; 2) появляются первые определения (2 кл.) – «Сложение одинаковых слагаемых называется умножением»; 3) некоторые понятия вводятся только с помощью термина (например, год, неделя, час, минута и др.); 4) описательное введение понятий (нумерация в пределах тысячи, меры длины); 5) некоторые понятия определяются генетически (окружность, 1 м Велика роль пропедевтики алгебраического и геометрического материала, особенно в 5-6 классах, где наряду с систематическим курсом арифметики изучаются начала алгебры и геометрии. Например, в учебнике Латотина Л.А., Чеботаревского Б.Д. «Математика 4»: геометрические понятия – окружность, круг, угол, смежные и вертикальные углы, прямоугольный параллелепипед, объем; алгебраические понятия - уравнение, выражение и его значение. Таким образом, в курсе математики ведется подготовка к изучению курсов алгебры и геометрии. Но не только на уроках математики, возможна пропедевтика и в других курсах, например, физики – понятие производной (мгновенная скорость), черчения – изображение пространственных фигур в стереометрии и др. В отдельных случаях, когда изучение понятия представляет собой существенные трудности, период первоначального ознакомления с понятием растягивается во времени, на протяжении которого учащиеся многократно сталкиваются с понятием, постепенно расширяя круг представлений о нем. Например, одно из важнейших понятий современного школьного курса математики - функция. Усвоение этого понятия возможно лишь при условии перехода от статического к диалектическому мышлению, что совершается не вдруг. Само понятие функция вводится в седьмом классе. Но в пятом и шестом классах сознание учащихся готовится к восприятию этого понятия. В качестве пропедевтики понятия функция в учебниках пятого и шестого классов рассматриваются различные упражнения. Функция как зависимость, закон соответствия, соответствие между отдельными элементами некоторых множеств проявляют себя в таких упражнениях, как составление выражений, отыскание значений выражения в зависимости от значений параметров, входящих в него. Функциональной пропедевтикой является изучение темы «Координатная плоскость». Психологические закономерности формирования математических понятий Формирование понятий - сложный психологический процесс, начинающийся с образования простейших форм познания - ощущений - и протекающий часто по следующей схеме: ощущения - восприятие - представление - понятие. Обычно разделяют этот процесс на две ступени: чувственную, состоящую в образовании ощущений, восприятия и представления, и логическую, заключающуюся в переходе от представления к понятию с помощью обобщения и абстрагирования. Чувственная ступень в процессе формирования понятий соответствует первому этапу пути познания вообще, то есть "живому созерцанию", и поэтому ее осуществление требует широкого применения наглядности. Если ученику никогда не показывали модель куба или предметы, имеющие форму куба, то у него не может образоваться представления, а следовательно, и понятия куба. Процесс формирования понятий будет эффективным, если он ориентирует учащихся на обобщение и абстрагирование существенных признаков (характеристического свойства) формируемого понятия. Рассмотрим процесс формирования понятий на примере понятия куба. Детям (6-7лет) показывают много предметов, отличающихся формой, размерами, окраской, материалом, из которого они сделаны, причем таких, что одни из них имеют форму куба, а другие нет. Дети, после того как им показывают на одно из этих тел и говорят, что это куб, безошибочно отбирают все те тела, которые имеют такую же форму, пренебрегая различиями, касающимися размера, окраски, материала. Здесь выделение из класса предметов подкласса, отождествление тел производится по одному еще недостаточно проанализированному признаку - внешней форме. Дети еще не знают свойств куба, они распознают его только по форме. Дальнейшая работа по формированию понятия куба состоит в анализе этой формы с целью выяснения ее свойств. Учащимся предлагают путем наблюдения найти, что есть общего у всех отобранных тел, имеющих форму куба, чем они отличаются от остальных. Устанавливается, что у каждого куба 8 вершин, 6 граней. Но у некоторых тел, которые мы не отнесли к кубам, тоже 8 вершин и 6 граней. Оказывается, у куба все грани - квадраты (эта работа обычно проводится после аналогичной работы по выделению класса квадратов из множества плоских фигур). Остается один шаг к образованию понятия куба - переход от представления к понятию путем абстрагирования, то есть отделения общих свойств от прочих, несущественных. Разумеется, на начальном этапе обучения нельзя еще говорить о полном абстрагировании этих свойств, у детей еще не образовывается понятие куба в чистом виде, они еще не определяют куб и противопоставляют его прямоугольному параллелепипеду с различными измерениями. В дальнейшем же, когда будет сконструирована логически упорядоченная система геометрических понятий (в рамках систематического курса геометрии), учащиеся узнают, что куб - это вид прямоугольного параллелепипеда. В этом - диалектика развития понятий. Приведенный пример показывает, что процесс формирования понятий, как правило, длительный процесс, способствующий развитию обобщающей и абстрагирующей деятельности учащихся. Однако формирование математических понятий не всегда протекает по приведенной выше схеме, начинающейся с ощущений. В частности, когда формируемое понятие связано, в той или иной форме, с категорией бесконечности (как, например, понятия прямой, плоскости, плотности множества рациональных чисел, предела и др.), то чувственная ступень играет меньшую роль, так как мы не в состоянии воспринимать бесконечное (ни в какой форме), и наглядность из средства, способствующего формированию понятия, иногда становится тормозящим фактором. Например, бесконечность множества рациональных чисел, лежащих между любыми двумя рациональными числами, не подкрепляется, а, наоборот, "опровергается" конкретным восприятием конечного отрезка, содержащего это множество. Свойство плотности множества рациональных чисел нельзя обнаружить опытным путем, оно не подтверждается наглядными геометрическими представлениями, а устанавливается логически. Этот и другие многочисленные примеры подтверждают выводы психологов о том, что восприятие наглядного материала в силу объективных особенностей этого материала может играть не только положительную, но и отрицательную роль.
|



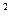 - это квадрат со стороной 1 м).
- это квадрат со стороной 1 м).