 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Похідні тригонометричних функцій
Похідні степеневих, показникових , логарифмічних і тригонометричних функцій. План.
1. Похідні степеневих функцій 2. Похідні показникових функцій 3. Похідні логарифмічних функцій 4. Похідні тригонометричних функцій
Рекомендована література.
Алгебра і початки аналізу: Підруч.для 10-11 кл.загальноосвіт.навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С.Дубинчук – К.: Зодіак-ЕКО, 2000.-608с. Розділ 10.§ 1,2,5.
Дайте письмові відповіді на запитання. Запишіть формули: 1. Похідні степеневих функцій 2. Похідні показникових функцій 3. Похідні логарифмічних функцій 4. Похідні тригонометричних функцій
Похідна степеневої функції Нам уже відомо, що Знайдемо похідну цієї функції, для цього зафіксуємо значення аргумента х0 і надамо йому приросту
1) 2) (Скориставшись формулою 3) Звідси
Розглянемо функцію у = хn-1, де Знайдемо похідну цієї функції, для цього зафіксуємо значення аргумента х0 і надамо йому приросту
1) 2)
3)
Отже, Таким чином виконується рівність:
Ми довели, що Розглянемо функцію Знайдемо похідну цієї функції:
Отже,
Похідна показникової функції Перш ніж знаходити похідну показниковїх функції, зробимо два важливих зауваження. Графік функції у=ах проходить через точку (0; 1). Нехай у у = ех якщо основа а показникової функції у = ах зростає від 2 до 3, то величина кута Таким чином, дотична до графіка функції у = ех в точці (0; 1) утворює з додатним напрямком осі абсцис, який дорівнює 450. У відповідності з геометричним змістом похідної даний висновок означає, що значення похідної функції Знайдемо тепер формулу похідної функції Нехай аргумент х0 одержав приріст
1) 2) 3)
Таким чином, похідна функції ех дорівнює самій функції: Знайдемо похідну функції
Отже, Похідна показникової функції дорівнює добутку цієї функції на натуральний логарифм її основи. Приклад 1. Знайдіть похідну функцій: а) у = 5х; б) у = е3-2х; в) Розв’язання а) б) в) г)
Похідна логарифмічної функції Розглянемо функцію Диференціюючи обидві частини цієї рівності, одержимо: Звідси Отже, Знайдемо похідну функції
Отже, Приклад 1. Знайдіть похідну функцій: а) в) а) б) в) г) =
Похідні тригонометричних функцій Знайдемо похідну функції у=
1) 2) 3)
Отже Аналогічно можна довести, що Знайдемо похідну функції Зафіксуємо х0 і надамо аргументу приросту
Отже, Аналогічно можна довести, що
|



 , де
, де 
 . А як знайти похідну функції у = х5, у = х20 тощо? Розглянемо функцію у= хn, де n –
. А як знайти похідну функції у = х5, у = х20 тощо? Розглянемо функцію у= хn, де n –  .
. , тоді:
, тоді: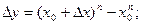





 .
.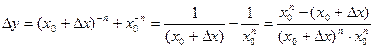



 =
=
 , де
, де  для
для  .
.
 .
.
 для всіх
для всіх  – величина кута , утвореного дотичною до графіка функції у = ах в точці (0; 1)з додатним напрямом осі абсцис. Величина цього кута залежить від значення основи а. Наприклад, обчислено, що при а = 2 величина кута
– величина кута , утвореного дотичною до графіка функції у = ах в точці (0; 1)з додатним напрямом осі абсцис. Величина цього кута залежить від значення основи а. Наприклад, обчислено, що при а = 2 величина кута  в точці х0 дорівнює
в точці х0 дорівнює  =1. Отже,
=1. Отже,  .
.

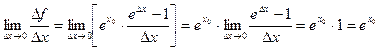 .
.
 , скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції:
, скориставшись основною логарифмічною тотожністю та правилом знаходження похідної складеної функції: .
.
 ; г)
; г)  .
. ;
; ;
; ;
;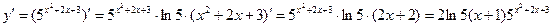 .
.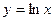 . За основною логарифмічною тотожністю:
. За основною логарифмічною тотожністю:  для всіх додатних х.
для всіх додатних х. , або
, або  .
. .
.
 . Так як
. Так як  , то
, то
 .
.
 ; б)
; б)  ;
; ; г)
; г)  .
.
 ;
;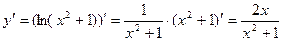 ;
; ;
;
 .
. . Зафіксуємо х0 і надамо аргументу приросту
. Зафіксуємо х0 і надамо аргументу приросту 


 .
.

 .
.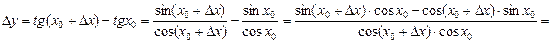
 .
.
 .
.
