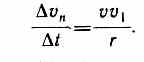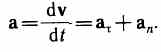ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Ускорение и его составляющие

123

В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.

Рассмотрим плоское движение,т. е. такое, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор v задает скорость точки

А в момент времени t. За время Dtдвижущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению и равную v₁=v + Dv. Перенесем вектор v₁ в точку А и найдем Dv (рис.4).

Средним ускорениемнеравномерного движения в интервале от t до t+Dt называется векторная величина, равная отношению изменения скорости Dv к интервалу времени Dt:

Мгновенным ускорением а(ускорением) материальной точки в момент времени t будет предел среднего ускорения:

Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.

Разложим вектор Dv на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор

AD, по модулю равный v₁. Очевидно, что вектор CD, равный Dv_t, определяет изменение скорости по модулю за время Dt: Dv_t=v₁- v. Вторая же составляющая вектора Dv-Dv_n характеризует изменение скорости за время Dt по направлению.

Тангенциальная составляющая ускорения

т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю. Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому As можно считать дугой окружности некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует Dv_n/AB = v₁/r, но так как AB = vDt, то

В пределе при Dt®0 получим v₁®v.

Поскольку v1®v, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между v и Dv_n стремится к прямому. Следовательно, при Dt®0 векторы Dv_n и v оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор Dv_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

называется нормальной составляющей ускоренияи направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).

Полное ускорениетела есть геометрическая сумма тангенциальной и нормальной составляющих (рис.5):

Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения — быстроту изменения скорости по направлению (направлена к центру кривизны траектории).

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

1) а_t=0, а_n = 0 — прямолинейное равномерное движение;

2) a_t=a=const, a_n=0 — прямолинейное равнопеременное движение. При таком виде движения

Если начальный момент времени t₁=0, а начальная скорость v₁=v₀, то, обозначив t₂ = t и v₂ = v, получим a = (v-v₀)/t, откуда

v =v₀+at.

Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, найдем, что длина пути, пройденного точкой, в случае равнопеременного движения

3) а_t=f(t), а_n=0 — прямолинейное движение с переменным ускорением;

4) а_t=0, а_n=const. При а_t=0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы а_n= v²/r следует, что радиус кривизны должен быть постоянным. Следовательно, движение по окружности является равномерным;

5) а_t=0, а_n¹0 — равномерное криволинейное движение;

6) a_t=const, a_n¹0—криволинейное равнопеременное движение;

7) a_t= f(t), a_n¹0 — криволинейное движение с переменным ускорением.

123