 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Правые и левые тройки векторов 7.1. В каком случае упорядоченную тройку некомпланарных векторов называют правой (левой)? 7.2. В каком случае перестановку векторов упорядоченной тройки называют циклической (ациклической)? Приведите примеры. 7.3. Изменяется ли ориентация упорядоченной тройки некомпланарных векторов при циклической (ациклической) перестановке? Приведите примеры.
Определение и свойства векторного произведения Векторов 7.4. Сформулируйте определение векторного произведения ненулевых векторов. 7.5. Как определяется векторное произведение векторов в случае, когда хотя бы один множитель - нулевой вектор? 7.6. Пусть 7.7. Найдите векторные произведения векторов: а) 7.8. В чем заключается геометрический смысл длины векторного произведения двух ненулевых векторов? 7.9. Как найти площадь параллелограмма, построенного на двух векторах? 7.10. Как найти площадь треугольника, построенного на двух векторах? 7.11. Каково векторное произведение двух коллинеарных векторов? Ответ обоснуйте. 7.12. Каково расположение двух ненулевых векторов, если известно, что их векторное произведение равно нулевому вектору? Ответ обоснуйте. 7.13. Чему равно векторное произведение ненулевого вектора на себя (векторный квадрат)? Повторите, чему равен скалярный квадрат вектора. 7.14. Обладает ли операция векторного произведения векторов свойством коммутативности? 7.15. В чем заключаются алгебраические свойства операции векторного произведения векторов? 7.16. По данным задания 7.6 найдите 7.17. Упростите выражения: а) б) в) 7.18. В чем заключается физический смысл векторного произведения двух ненулевых векторов?
Выражение в декартовых координатах 7.19. Как найти координаты векторного произведения двух векторов по их координатам в прямоугольном базисе? 7.20. Пусть в прямоугольном базисе а) 7.21. Найдите площадь параллелограмма, построенного на векторах 7.22. Найдите площадь треугольника с вершинами 7.23. Найдите высоту 7.23. Сила
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
7.24. Сформулируйте определение смешанного произведения векторов. 7.25. В чем заключается геометрический смысл смешанного произведения векторов? 7.26. Как, найти объем параллелепипеда, построенного на трех некомпланарных векторах? 7.27. Как найти объем пирамиды, построенной на трех некомпланарных векторах? 7.28. Чему равно смешанное произведение трех компланарных векторов? 7.30. Каково расположение трех ненулевых векторов, если известно, что их смешанное произведение равно нулю? 7.31. Сформулируй признак компланарности векторов. 7.32. Как изменяется величина смешанного произведения при циклических и ациклических перестановках векторов? 7.33. Пусть в прямоугольном базисе 7.34. Как найти смешанное произведение векторов по их координатам в прямоугольном базисе? 7.35. Найдите смешанное произведение векторов 7.36. Найдите объем тетраэдра с вершинами 7.38. Лежат ли точки
|



 ,
,  , а угол между этими векторами равен
, а угол между этими векторами равен  . Вычислите
. Вычислите 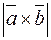 .
. ; б)
; б) 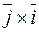 ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.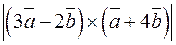 .
. ;
; ;
; .
. ,
,  . Найдите:
. Найдите: ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. и
и  .
. ,
,  ,
,  .
. треугольника из задания 7.22
треугольника из задания 7.22 приложена к точке
приложена к точке  . Найдите момент этой силы относительно точки
. Найдите момент этой силы относительно точки  .
. . Пользуясь определением, найдите смешанное произведение этих векторов.
. Пользуясь определением, найдите смешанное произведение этих векторов. ,
,  ,
,  . Какова ориентация тройки
. Какова ориентация тройки  ?
? и высоту, проведенную из вершины
и высоту, проведенную из вершины  на плоскость
на плоскость  .
. в одной плоскости?
в одной плоскости?