ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Графічне розв’язання задачі лінійного програмування за допомогою Excel.

Лабораторна робота №3.

Тема. Розв’язання графічним методом задачі лінійного програмування.

Мета: набуття навиків побудови математичної моделі задачі лінійного програмування, вивчення графічного методу для знаходження її розв’язку та оволодіння навиками побудови таблиць та діаграм (графіків) в Excel.

Порядок роботи:

1. Записати математичну модель задачі оптимального планування виробництва згідно заданого варіанту.

2. Використовуючи засоби створення діаграм Excel, намалювати відповідну таблиці діаграму.

3. Знайти максимальне та мінімальне значення цільової функції на побудованій діаграмі.

4. Проінтерпретувати отримані результати для вихідної задачі.

5. Оформити звіт для захисту лабораторної роботи за зразком

· назва роботи

· мета роботи

· порядок роботи

· короткі теоретичні відомості

· алгоритм розв’язку задачі

· малюнки відповідних таблиць та діаграм

· аналіз отриманих результатів та висновки.

Довідковий матеріал.

Перш ніж розглянути приклад графічного розв’язання задачі лінійного програмування, розглянемо графічне розв’язання нерівності і системи нерівностей.

Графічне розв’язання нерівності.

Приклад 1

Нехай дано нерівність x₁ + 2x₂ £ 4. Розв’яжемо цю нерівність графічно.

Побудуємо на площині рівняння прямої, що відповідає нерівності x₁ + 2x₂ = 4. Для побудови прямої досить знати дві довільні точки, що належать цій прямій. Знайдемо ці точки.

Для цього візьмемо довільне значення x₁, наприклад, x₁ = 0 та підставимо у рівняння. Тоді

0 + 2x₂ = 4Þ x₂ = 2. Перша точка (0; 2). Візьмемо друге x₁, наприклад, x₁ = 4 та підставимо у рівняння. Тоді 4 + 2x₂ = 4Þ x₂ = 0. Друга точка (4; 0). Маємо дві точки на координатній площині, через які проводимо пряму.

Пряма розбиває площину на дві півплощини. Розв’язанням нерівності є одна з півплощин. Підставимо в нерівність довільну точку площини (найпростіше, точку (0; 0)). Якщо нерівність правильна, то розв’язком є півплощина, що містить цю точку. Якщо нерівність неправильна, то розв’язком є інша півплощина. На рисунку півплощину, яка є розв’язком, позначають штрихуванням.

Підставимо в нашу нерівність точку (0; 0): 0£4 – виконується. Отже, розв’язком нерівності буде півплощина, що містить цю точку.

Тепер розв’яжемо графічно систему нерівностей.

Дано систему нерівностей:

Для того, щоб розв’язати графічно систему нерівностей, потрібно розв’язати графічно кожну нерівність. Пронумеруємо нерівності:

Нерівності (4) і (5) показують, що область розв’язків системи знаходиться в першій чверті координатної площини.

Розв’яжемо графічно нерівності (1), (2) і (3). Областю розв’язків системи нерівностей буде та область площини, у якій перетинаються півплощини розв’язків кожної нерівності. У нашому прикладі областю розв’язків системи нерівностей є багатокутник ABCDE.

Графічне розв’язання задачі лінійного програмування

Приклад 2

Нехай необхідно знайти (x₁, x₂ ), при яких функція L = 2x₁ + x₂ досягає максимуму, причому x₁, x₂ повинні задовольняти наступній системі обмежень:

Розв’язання:

Будуємо область розв’язків системи обмежень. Область розв’язків – багатокутник ABCDE, побудова якого відбулася раніше.

Знаходимо градієнт функції L: . Будуємо вектор з початком у точці (0; 0) і кінцем у точці (2; 1).

Примітка: вектор можна збільшувати, чи зменшувати пропорційно:

Будуємо пряму, перпендикулярну вектору градієнта. Пересуваємо цю пряму в напрямку, зазначеному вектором. Остання точка області, що перетинає пряма і є точкою максимуму. У даному випадку це точка D.
Знаходимо координати точки максимуму. Ця точка лежить на перетинi прямих (2) і . Розв'язуємо систему рівнянь:

Одержали: x_1max = 10; x_2max = 0.

Обчислюємо максимальне значення цільової функції:

L_max = 2×10 + 0 = 20.

Відповідь: максимального значення L=20 цільова функція досягає в точці (10; 0).

Задача на знаходження мінімуму відрізняється від попередньої тим, що необхідно знайти такі (x₁, x₂ ), при яких функція L досягає мінімуму за даної системи обмежень. Розв’язання аналогічне до випадку максимуму, за винятком того, що пряму пересувають у напрямку, протилежному до вектора градієнта.

Для цього прикладу мінімум досягається в точці А. Ця точка лежить на перетинанні прямих (1) і x₁ = 0. Вирішуємо систему рівнянь:

Одержали: x_1min = 0; x_2min = 2.

Визначимо мінімальне значення цільової функції:

L_m_in = 2×0 + 2 = 2.

Відповідь: мінімального значення L=2 цільова функція досягає в точці (0; 2).

Графічне розв’язання задачі лінійного програмування за допомогою Excel.

MS Excel – є програмою для розрахунків за допомогою електронних таблиць. Головна область її застосування – виконання розрахунків, як в бізнесі так і у повсякденному житті. Excel має велику кількість вбудованих функцій, різні засоби обробки даних, багато сервісних засобів, мета яких полегшити роботу користувачеві.

Excel дозволяє створювати наочні діаграми для графічного представлення чисельних залежностей у робочих таблицях. Після розміщення даних у робочій таблиці, для створення діаграми необхідно показати Excel, яку інформацію використати, який тип графіку потрібний і де його треба розташувати. Це можна зробити за допомогою Chart Wizard (експерт по функціях), який складається з п’яти кроків.

Перед викликом Chart Wizard необхідно вибрати інтервал комірок, в яких знаходиться інформація потрібна для діаграми. Таблиця має бути стандартною та суцільною. Для створення графіку:

§ натисніть на інструменті Chart Wizard на панелі стандартного інструментарію;

§ курсором, який змінить свій вигляд необхідно відмітити місце розташування та розмір діаграми. Якщо діаграму необхідно розмістити на іншому робочому листі, натисніть на потрібному корінці листа і виділіть на ньому потрібні контури;

§ на першому кроці потрібно вказати інтервал комірок потрібної таблиці. Якщо комірки були відмічені, тоді у полі Range (інтервал) інтервал буде вже вписаний. При потребі його можна замінити;

§ діалогове вікно кроку 2 допоможе вибрати тип діаграми;

§ діалогове вікно кроку 3 надасть різні варіанти вибраного типу діаграми;

§ у діалоговому вікні кроку 4 Chart Wizard покаже вигляд вибраної діаграми. У полі Data Series in (ряди даних) необхідно вказати, що потрібні дані, за якими будується діаграма знаходяться у рядках чи колонках;

§ в діалоговому вікні кроку 5 необхідно ввести у відповідні поля назву діаграми, якщо потрібно, пояснення до діаграми, заголовки осей, осі категорій Х та У.

§ після проходження всіх кроків необхідно натиснути кнопку Finish.

Розмір та місце розташування діаграми можна змінювати. Зафіксувавши курсор миші на одній з точок, що оточують графік, і перетягнувши у потрібний бік змінимо розмір, а навівши курсор на діаграму і, не відпускаючи натисненої лівої кнопки миші, можна перемістити цілу картинку у потрібне місце.

Після подвійного натиску на діаграмі, з’являється рамка фрейму. Тепер одним натиском на об’єкті можна його виділити, і за допомогою контекстного меню, редагувати об’єкт за своїм бажанням.

Розглянемо приклад розв’язання задачі в Excel. Щоб отримати схожий результат при розв’язуванні свого варіанту, необхідно:

Побудувати графіки обмежуючих прямих:

· визначити точки перетину прямих з осями координат;

· записати таблиці даних для кожної прямої;

· визначити точки перетину прямих.

Позначити множину допустимих розв’язків.
Обчислити значення цільової функції в крайніх точках.
Вказати максимальне та мінімальне значення цільової функції.

Приклад

Зауваження: для знаходження точок перетину рівнянь обмежень використовуйте метод оберненої матриці, для побудови області допустимих значень, використовуйте поточкову діаграму (ряди в стовбцях).

Індивідуальне завдання:

(для визначення числових значень коефіцієнтів використовується N – порядковий номер студента в списку студентів групи)

Розглянемо діяльність деякого виробничого об’єкта. Нехай у його розпорядженні є 5 типів сировинних ресурсів у розмірі ( - кількість одиниць ресурсу і). З цих ресурсів виробничий об’єкт виготовляє 2 види продукції в ціні 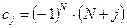за одиницю. Задано матрицю А з елементами - кількість одиниць ресурсу і необхідних для виготовлення однієї одиниці продукції j.

, якщо ; , якщо

Визначити оптимальний план виробництва.