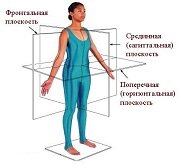
 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основные свойства дивергенции
Вычисление криволинейного интеграла 2-го рода. Пусть ориентированная кривая L задана параметрическими уравнениями x = j (t), y=y (t), a ? t ?b, где j (t), y (t) - непрерывно дифференцируемые на отрезке [a, b ] функции. Тогда
Пределы интегрирования выбираются в соответствии с ориентацией кривой L: если ориентации кривой L соответствует изменение параметра t от a доb, то в формуле (29) выбирается первый вариант пределов интегрирования. В противном случае в (29) нужно выбирать вариант пределов интегрирования в скобках. Пусть кривая L задана явно уравнением y=h(x), a? x ?b, где h (x) - непрерывно дифференцируемая на отрезке [a, b] функция. Тогда
Пределы интегрирования выбираются в соответствии с ориентацией кривой L,как в формуле (29). Пусть кривая L задана явно уравнением x=h(y), a? y ?b, где h (y) - непрерывно дифференцируемая на отрезке [a, b] функция. Тогда
Пределы интегрирования выбираются в соответствии с ориентацией кривой L,как в формуле (29). 16. Независимость криволинейного интеграла от пути интегрирования. Среди силовых полей в физике особую роль играют так называемые потенциальныесиловые поля. Их отличительной особенностью является то, что работа, совершаемая таким полем, зависит лишь от начальной и конечной точек пути, и не зависит от траектории, соединяющей эти точки. Математически это соответствует тому, что криволинейный интеграл второго рода также зависит лишь от начальной и конечной точек пути, и не зависит от траектории, соединяющей эти точки. Поэтому с математической точки зрения представляет интерес выяснение тех условий, при выполнении которых криволинейный интеграл обладает этим свойством. Плоский случай Пусть дан криволинейный интеграл второго рода по плоской кривой
Ответ на поставленный вопрос дают следующие две теоремы. Теорема 1. Для того чтобы
Теорема 2.Если в односвязной области существуют и непрерывны
Пространственный случай В случае интегралов по пространственной кривой соответствующие теоремы приобретают следующий вид. Теорема 1. Для того чтобы Для формулировки второй теоремы введем понятие роторавекторной функции. Пусть
Теорема 2.Для того чтобы
17. Формула Грина. Если в плоской области D, ограниченной линией L, задано векторное поле
Рис. 4 При этом L считается ориентированной в положительном направлении, то есть обход вдоль L осуществляется так, чтобы область D оставалась слева. Эта формула справедлива не только для односвязных областей (как на рисунке), но и для многосвязных областей, границы которых состоят из нескольких компонент (например, кольцо). Формула Грина позволяет свести циркуляцию к двойному интегралу. 18. Тройной интеграл в декартовых координатах. Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов.
Тогда для любой непрерывной в области U функции f(x,y,z) можно записать соотношение ∭Uf(x,y,z)dV=∬D⎡⎣⎢⎢∫z1(x,y)z2(x,y)f(x,y,z)dz⎤⎦⎥⎥dA. Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла, в котором подынтегральной функцией является однократный интеграл. В рассмотренном случае сначала вычисляется внутренний интеграл по переменной z, а затем − двойной интеграл в области D по переменным x и y. x=a,x=b,y=f1(x),y=f2(x), где f1(x), f2(x) − непрерывные функции в интервале [a,b] и f1(x)≤f2(x), то, записывая двойной интеграл в виде повторного, получаем ∭Uf(x,y,z)dV=∫abdx∫f1(x)f2(x)dy∫z1(x,y)z2(x,y)f(x,y,z)dz.(1) В другом случае, когда область D(x,y) относится к типу II (является элементарной относительно оси Ox) и ограничена линиями y=c,y=d,x=φ1(y),x=φ2(y), где φ1(y), φ2(y), − непрерывные на отрезке [c,d] функции, причем φ1(y)≤φ2(y), тройной интеграл представляется в виде ∭Uf(x,y,z)dV=∫cddy∫φ1(y)φ2(y)dx∫z1(x,y)z2(x,y)f(x,y,z)dz.(2) Формулы (1) и (2) называются формулами сведения тройного интеграла к повторному. ∭Uf(x,y,z)dxdydz=∫abdx∫cddy∫pqf(x,y,z)dz. Если исходная область интегрирования U, более сложная, чем рассмотренная выше, то ее нужно разбить на конечное число более простых областей, в которых уже можно вычислить тройные интегралы методом сведения к повторным. 19. Тройной интеграл в цилиндрических координатах. Рассмотрим цилиндрическую систему координат: Оrφz, которая совмещена с декартовой системой координат Оxyz(рис. 2.19)
При этом Вычислим Якобиан перехода от декартовой системы к цилиндрической:
Следовательно, Тогда тройной интеграл примет вид:
20. Тройной интеграл в сферических координатах. Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где ρ − длина радиуса-вектора точки M;
Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга.
Якобиан перехода от декартовых координат к сферическим имеет вид:
Раскладывая определитель по второму столбцу, получаем
Соответственно, абсолютное значение якобиана равно
Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:
Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования U представляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет вид f (x2 + y2 + z2).
В этом случае якобиан равен 21. Поверхностный интеграл 1-ого и 2-ого типа. Если f(x, y, z) — функция, определенная и непрерывная в точках поверхности Σ, то поверхностным интегралом I роданазывается выражение
Значение интеграла I рода не зависит от выбора стороны поверхности.
Пусть Σ+ — сторона поверхности Σ, задаваемая направлением нормали n={cosα; cosβ; cosγ};P(x,y,z),Q(x,y,z),R(x,y,z)— функции, определенные и непрерывные на поверхности Σ. Поверхностным интегралом II рода называют выражение Для поверхности, заданной параметрически,
где 22. Формула Стокса в координатной форме. Связь между поверхностными и криволинейными интегралами II рода выражает следующая теорема. Теорема.Если функции
где Формула (1) называется формулой Стокса. Из формулы Стокса вытекает, что если выполняются условия
то криволинейный интеграл по произвольному замкнутому пространственному контуру
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла. 23. Формула Остроградского-Гаусса в координатной форме. Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью, выражает следующая теорема. Теорема.Если функции
где Формула (1) является аналогом формулы Остроградского-Грина и называетсяформулой Остроградского-Гаусса.
плоскость Рассмотрим тройной интеграл
Двойные интегралы в правой части полученного равенства, используя формулу Тогда,
По свойству 5 , интеграл
или
где Аналогично доказываются формулы
Складывая почленно равенства (2), (3) и (4), получим формулу (1)Остроградского-Гаусса. 24. Скалярное и векторное поле. Скалярным полем называется часть пространства, каждой точке которого поставлена в соответствие определённое число – скаляр. Примеры скалярных полей: 1) поле температур внутри неоднородно нагретого тела; 2) поле давлений воздуха в атмосфере; 3) поле плотности вещества в теле; 4)поле плотности распределения электрического заряда и т.д. Скалярное поле считается заданным, если в каждой точке Mнекоторой области W определена скалярная функция U(M). В связи с этим, понятие скалярного поля и функции, определенной в области W, эквивалентны. Если скалярное поле отнесено к декартовой системе координат, то скалярную функцию U(M) можно записать, например, в виде функции двух U(x,y) или трёх U(x,y,z) переменных. Простейшей геометрической характеристикой скалярного поля U(M) являются поверхности уровня. Поверхности уровня – это геометрическое место точек, в которых скалярная функция принимает постоянные значения, т.е. U(x,y,z)=C,где С – произвольная постоянная. В случае двумерного поля понятие поверхности уровня заменяется понятием линии уровня: U(x,y)=C.
25. Векторная функция скалярного аргумента. Если каждому значению параметра t из некоторого промежутка
Откладывая вектор Проекции вектора
Производная от вектора
а вторая производная соответственно:
Если параметр t – это время, то векторное уравнение (4) называют уравнением движения. Тогда вектор-производная называется скоростью движения:
Скорость движения – это вектор, направленный по касательной к траектории движения (годографу) в соответствующей точке в сторону возрастания параметраt. Вектор
называется ускорением движения. 26. Дивергенция векторного поля. Дивиргенция (или расходимость) векторного поля
Þ Основные свойства дивергенции 1. 2. В каждой точке § если § если § если 3.
Воспользуемся формулой Остроградского—Гаусса, связывающей интеграл по замкнутой поверхности с интегралом по объёму, ограниченному этой поверхностью:
Применяемтеорему о среднем к тройному интегралу:
где М1 — это некоторая фиксированная точка в объёме, ограниченном замкнутой поверхностью (σ),
Теперь используем определение (1) дивергенции:
так как при 4. Если использовать понятие дивергенции, то теорема Остроградского-Гаусса в векторной форме:
то есть поток вектора Так как Учитывая это, смысл теоремы Остроградского-Гаусса в форме (3) можно сформулировать следующим образом: поток векторного поля Следовательно, если поток равен 0, то внутри поверхности 5. Линейность дивергенции:
Это следует из линейности операций сложения векторов и дифференцирования. 6. Дивергенция прозведения скалярного поля
w
27. Поток векторного поля. Пусть имеем векторное поле
координаты которого P,Q,R – непрерывны в некоторой области G трёхмерного пространства. Пусть в G задана гладкая или кусочно-гладкая ориентируемая поверхность S. Определение. Потоком П векторного поля
где
В случае замкнутой поверхности будем всегда выбирать внешнюю нормаль Если
где 28. Вихрь векторного поля. Ротором или вихрем векторного поля
Основные свойства ротора 1.
w
Из физики известно, что Поэтому то есть поле линейных скоростей тела, вращающегося вокруг неподвижной оси есть плоское векторное поле. Вычислим его ротор равен:
Следовательно, ротор этого поля В технической литературе ротор векторного поля часто называют вихрем этого поля. 29. Циркуляция векторного поля. Циркуляцией Ц векторного поля а=а(М) называется линейный интеграл, взятый вдоль замкнутой ориентированной кривой L. Таким образом, по определению
где символ Если векторное поле а=а(М) задано в координатой форме a=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k то циркуляция векторного поля будет равна
За положительное направление обхода замкнутой кривой L будем считать направление, при котором область, ограниченная этой кривой, будет оставаться слева. 30. Формула Стокса в векторной форме. Теорема. Пусть Замечание 1. Равносильная формулировка: Замечание 2. В случае плоской кривой Замечание 3. Формулы в правой части запомнить непросто. Поэтому удобно записать подынтегральное выражение в виде определителя Разумеется, это не совсем обычный определитель. Ведь во второй строке его стоят операторы дифференцирования. Поэтому условимся считать, что мы понимаем под этим определителем его формальное разложение по первой строке, причем произведение, например, оператора Доказательство теоремы. Вычислим, например, Тогда Аналогично, Формула Стокса доказана. Векторная запись формулы Стокса. Вспомним, что При этом правая часть формулы Стокса принимает вид 31. Формула Остроградского-Гаусса в векторной форме. Пусть Σ — кусочно-гладкая поверхность, ограничивающая объем V, и P(x, y, z), Q(x, y, z), R(x, y, z) — функции, непрерывные вместе со своими частными производными на области V. Тогда имеет место формула
где cos α, cos β, cos γ — направляющие косинусы внешней нормали к поверхности. Если функции P, Q, R рассматривать как компоненты вектор-функции F, то формула Остроградского—Гаусса может быть записана в векторной форме:
где n = (cos α, cos β, cos γ). 32. Соленоидальное и потенциальное поле. Векторное поле Fназываетсяпотенциальным, если оно является градиентом некоторого скалярного поля U, т.е. F = gradU В случае если поле F
что равносильно тому, что выражение Теорема. Пусть область
Приведенная теорема утверждает, что векторное поле F потенциально тогда и только тогда, когда rot F = 0, т.е. поле является безвихревым. Условие rot F = 0 является также необходимым и достаточным условием того, что криволинейный интеграл
не зависит от формы кривой, соединяющей точки А и В в области
Если поле F потенциально, то его потенциал U можно найти непосредственным интегрированием по некоторому пути
При этом, в силу независимости этого интеграла от формы пути, путь
где каждый из интегралов – есть обычный определенный интеграл по соответствующей переменной, а остальные переменные играют роль констант. Если потенциал векторного поля F известен, то
Векторное поле F называется соленоидальным, если оно является ротором некоторого векторного поля А, т.е.F Теорема. Пусть область div F в каждой точке области Если векторное поле соленоидально, то его поток через любую замкнутую поверхность равен нулю.
|
 .(29)
.(29) . (30)
. (30) . (31)
. (31) .
. , что
, что .
. и
и  , то для того, чтобы было выполнено условие теоремы 1, необходимо и достаточно, чтобы
, то для того, чтобы было выполнено условие теоремы 1, необходимо и достаточно, чтобы .
. не зависел от пути интегрирования необходимо и достаточно, чтобы существовала такая функция,
не зависел от пути интегрирования необходимо и достаточно, чтобы существовала такая функция,  что
что  .
. . Тогда ротор этой функции определяется так:
. Тогда ротор этой функции определяется так:
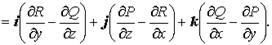
 .
.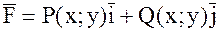 , где P и Q имеют непрерывные частные производные, то имеет место формула Грина:
, где P и Q имеют непрерывные частные производные, то имеет место формула Грина:
 .
.






 на плоскость Oxy и осью Ox;
на плоскость Oxy и осью Ox;


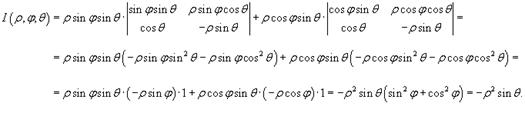



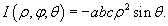
 , определяемое равенством:
, определяемое равенством: .
. , определяемое равенством
, определяемое равенством 
 ,
, , а знак выбирается в зависимости от направления нормали. При переходе к другой стороне Σ– поверхности Σ интеграл II рода меняет знак на противоположный.
, а знак выбирается в зависимости от направления нормали. При переходе к другой стороне Σ– поверхности Σ интеграл II рода меняет знак на противоположный. непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности
непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности  , то имеет место формула
, то имеет место формула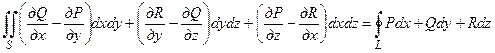 , (1)
, (1) – граница поверхности
– граница поверхности  ,
,  ,
,  ,
, .
. , то имеет место формула
, то имеет место формула , (1)
, (1)
 , уравнение которой
, уравнение которой  ; сверху – поверхностью
; сверху – поверхностью  , уравнение которой
, уравнение которой  ; сбоку – цилиндрической поверхностью
; сбоку – цилиндрической поверхностью 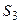 , образующие которой параллельны оси
, образующие которой параллельны оси  (см. рис. 10). Функции
(см. рис. 10). Функции  ,
,  непрерывны в замкнутой области
непрерывны в замкнутой области  – проекции области
– проекции области  ,
,  .
. .
. , заменим поверхностными интегралами II рода по внешней стороне поверхностей
, заменим поверхностными интегралами II рода по внешней стороне поверхностей  .
. по внешней стороне
по внешней стороне  ,
, , (2)
, (2) , (3)
, (3) . (4)
. (4) Примеры линий уровня: 1) на топографических картах линии, соединяющие точки, имеющих одну и туже высоту над уровнем моря; 2) в термодинамике на диаграммах состояния линии, соединяющие точки, имеющих одну и туже температуру (изотермы), давление (изобары) или объём (изохоры); 3) в электростатике линии, соединяющие точки, имеющие одинаковый потенциал (эквипотенциальные линии).
Примеры линий уровня: 1) на топографических картах линии, соединяющие точки, имеющих одну и туже высоту над уровнем моря; 2) в термодинамике на диаграммах состояния линии, соединяющие точки, имеющих одну и туже температуру (изотермы), давление (изобары) или объём (изохоры); 3) в электростатике линии, соединяющие точки, имеющие одинаковый потенциал (эквипотенциальные линии). ставится в соответствие по некоторому правилу fопределенный вектор, то говорят, что задана вектор-функция скалярного аргумента t:
ставится в соответствие по некоторому правилу fопределенный вектор, то говорят, что задана вектор-функция скалярного аргумента t: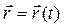 . (4)
. (4) при
при  от начала координат, получаем траекторию движения конца вектора, называемую годографом.
от начала координат, получаем траекторию движения конца вектора, называемую годографом. .
. ,
, ,
, , (5)
, (5) . (6)
. (6) в точке
в точке 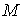 — это предел отношения потока вектора
— это предел отношения потока вектора  через замкнутую поверхность
через замкнутую поверхность  , окружающую точку
, окружающую точку 

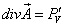 — дивергенция является производной потока через замкнутую ориентированную поверхность по объёму, ограниченному этой поверхностью.
— дивергенция является производной потока через замкнутую ориентированную поверхность по объёму, ограниченному этой поверхностью.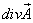 — это дифференциальнаяхарактеристика поля, является скалярной величиной.
— это дифференциальнаяхарактеристика поля, является скалярной величиной.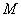 поля
поля  показывает наличие источников или стоков поля:
показывает наличие источников или стоков поля: , то в точке
, то в точке  численно равно мощности источника;
численно равно мощности источника; , то в точке
, то в точке  численно равно мощности стока;
численно равно мощности стока; , то в точке
, то в точке  вычисляется по формуле:
вычисляется по формуле:

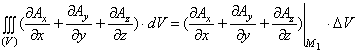
 —величина этого объёма.
—величина этого объёма. ,
, точка M1стремится к точке M. v
точка M1стремится к точке M. v ,
,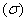 равен тройному интегралу от дивергенции вектора
равен тройному интегралу от дивергенции вектора  равен суммарной мощности источников и стоков по объему
равен суммарной мощности источников и стоков по объему  .
. .
. на векторное поле
на векторное поле  вычисляется по формуле:
вычисляется по формуле: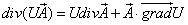 .
. Þ
Þ 

 ,
, через ориентируемую поверхность S называется
через ориентируемую поверхность S называется
 единичный вектор нормали
единичный вектор нормали  к выбранной стороне поверхности S;
к выбранной стороне поверхности S; – элемент площади поверхности S.
– элемент площади поверхности S. углы, которые образует с осями координат OX, OY, OZ нормаль
углы, которые образует с осями координат OX, OY, OZ нормаль 

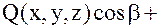



 ,
, ,
, 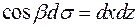 ,
, 
 называется вектор с проекциями
называется вектор с проекциями
 — это векторная величина, которая является дифференциальной (т.е. точечной) характеристикой векторного поля
— это векторная величина, которая является дифференциальной (т.е. точечной) характеристикой векторного поля  — свойство линейности.
— свойство линейности. .
.
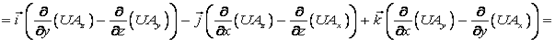



 v
v
 твердого тела (материальной точки M), вращающегося вокруг оси
твердого тела (материальной точки M), вращающегося вокруг оси  с постоянной угловой скоростью
с постоянной угловой скоростью  .
.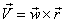 , где
, где  - это угловая скорость вращения,
- это угловая скорость вращения,  - это радиус вектор точки М.
- это радиус вектор точки М.
 то есть
то есть  ;
; характеризует вращательную способность поля
характеризует вращательную способность поля 
 означает интеграл по замкнутой кривой L.
означает интеграл по замкнутой кривой L.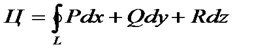
 - гладкая ориентированная двусторонняя поверхность (т.е. направление нормали выбрано) и
- гладкая ориентированная двусторонняя поверхность (т.е. направление нормали выбрано) и  - кусочно гладкая кривая, ограничивающая
- кусочно гладкая кривая, ограничивающая  - непрерывно дифференцируемые. Тогда
- непрерывно дифференцируемые. Тогда  .
.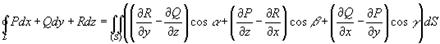 .
. и функций
и функций  эта формула совпадает с формулой Грина.
эта формула совпадает с формулой Грина. .
. на функцию
на функцию  есть
есть  и т.п.
и т.п. . Пусть, для простоты,
. Пусть, для простоты,  - уравнение
- уравнение  кривой
кривой  :
:  (разумеется,
(разумеется,  - непрерывно дифференцируемые функции).
- непрерывно дифференцируемые функции).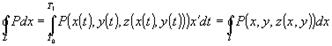 . К плоской кривой
. К плоской кривой 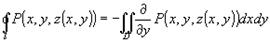 , где
, где  - ограничиваемая кривой
- ограничиваемая кривой  . Итак,
. Итак,  . Далее,
. Далее,  ,
,  , и, значит,
, и, значит, 
 . Поэтому
. Поэтому  .
. ,
,  и
и 

 .
. , где
, где  - направляющие косинусы к выбранной стороне.
- направляющие косинусы к выбранной стороне.
 или
или  . Итак, в сделанных выше предположениях теорема Стокса выглядит так:
. Итак, в сделанных выше предположениях теорема Стокса выглядит так:  .
.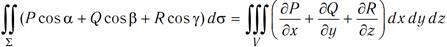 ,
,
 .
.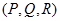 потенциально, выполняются равенства
потенциально, выполняются равенства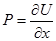 ,
,  ,
,  ,
, является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции  . Эта функция называется потенциалом векторного поля F.
. Эта функция называется потенциалом векторного поля F. поверхностно односвязна и функции
поверхностно односвязна и функции  – непрерывно дифференцируемы в
– непрерывно дифференцируемы в  ,
,  ,
,  .
.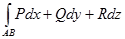
 .
.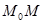 :
: .
. , вдоль каждого из звеньев которой изменяется лишь одна координата, а остальные остаются постоянными. В этом случае два из трех дифференциалов в криволинейном интеграле обращаются в ноль, и потенциал вычисляется в виде суммы:
, вдоль каждого из звеньев которой изменяется лишь одна координата, а остальные остаются постоянными. В этом случае два из трех дифференциалов в криволинейном интеграле обращаются в ноль, и потенциал вычисляется в виде суммы: ,
, .
. rot A
rot A  A. Поле А называется векторным потенциалом поля F.
A. Поле А называется векторным потенциалом поля F.