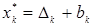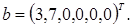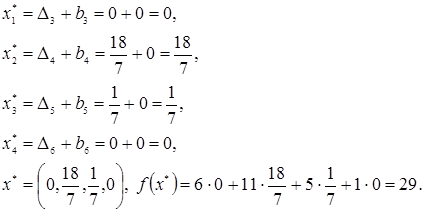ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример решения задачи симплекс-методом
Симплекс-метод Симплекс-метод является основным численным методом решения задач ЛП в канонической форме, т.е. в виде
Систему линейных уравнений
где
Пусть ранг матрицы Пусть множество Теорема 2 (признак оптимальности опорного плана). Опорный план
При этом Теорема 3 (признак неограниченности целевой функции). Если Теорема 4 (о возможности улучшения опорного плана). Если опорный план Переход от одного опорного плана 1) выбирают разрешающий столбец 2) выбирают разрешающую строку, соответствующую наименьшему отношению элементов столбца свободных членов системы ограничений к соответствующим положительным элементам разрешающего столбца —
где минимум берется по всем номерам Затем систему ограничений Пусть линейно независимы первые
Тогда симплекс-таблица имеет вид:
Слева в таблице указаны базисные переменные
Пример решения задачи симплекс-методом
Проиллюстрируем решение задачи ЛП симплекс-методом на примере решения задачи (4.1)–(4.2), ранее решенной геометрически. Задачу (4.1)–(4.2) запишем в каноническом виде, введя три дополнительные переменные
Пара двойственных задач Парой (симметричных) взаимно двойственных задач называются задачи f (x) = (c, x) → max, g (y) = (bТ, y) → min, Ax ATy x где с, x Задачи (4.10) и (4.11) взаимно двойственны, т.е. если прямая задача является задачей максимизации и все неравенства вида « Если задача ЛП сформулирована в канонической форме: f (x) = (c, x) → max, Ax=b, (4.12) x то двойственная к ней задача имеет вид: g (y) = (bT, y) → min, ATy и наоборот. Справедливы следующие основные теоремы, устанавливающие связь между оптимальными решениями взаимно двойственных задач. Теорема 5. (Первая теорема двойственности). Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т.е. f (x*) = g (y*). Если же целевая функция одной из пары двойственных задач не ограничена, то другая задача вообще не имеет допустимых планов. Теорема 6. (Вторая теорема двойственности). Для того, чтобы допустимые планы x*, y* прямой (4.10) и двойственной (4.11) задач были оптимальными, необходимо и достаточно, чтобы выполнялись условия:
т.е. если х*j > 0, то если Следовательно, если в оптимальном плане х* какая-либо компонента x*j > 0, то соответствующее ей j-ое ограничение двойственной задачи на её оптимальном плане y* обращается в равенство; если оптимальный план х* обращает i-ое ограничение этой задачи в строгое неравенство, то соответствующая ему компонента y*i в оптимальном плане двойственной задачи равна нулю. Задача 3. Дана задача ЛП: f (x)=6x1+11x2+5x3+x4→ min, (4.15)
Требуется: - сформулировать двойственную задачу к задаче (4.15)-(4.16); - решить двойственную задачу геометрически и симплекс-методом; - найти оптимальное решение прямой задачи (4.15)–(4.16), используя теоремы двойственности. Сформулируем задачу, двойственную к задаче (4.15)–(4.16). Прямая задача: f (x)=(c,x)=6x1+11x2+5x3+x4→ min,
Двойственная задача, по определению, будет иметь вид: g (y) = (bТ, y)=3y1+7y2 →max,
y1 Окончательно, в скалярной форме, задача, двойственная к задаче (4.15)–(4.16), имеет вид: g (y) = (bТ, y)=3y1+7y2 →max,
Полученная задача имеет две переменные y1, y2 , поэтому можно найти её решение геометрически (рис. 3).
Рис. 3 Множество R — пятиугольник OABCD. Строим линии уровня целевой функции g(y)=3y1+7y2 = const и перемещаем их в направлении вектора grad g(y)=(3;7). Оптимальной вершиной является точка С, координаты которой определим из решения системы уравнений:
Итак, y*1=5; y*2=2; max g (y) = g(y*) = 3·5+7·2 = 29. Зная оптимальный план двойственной задачи, найдём оптимальный план исходной задачи x*, используя теоремы двойственности. По теореме 5 можно утверждать, что прямая задача (4.15) – (4.16) имеет оптимальный план x*, на котором целевая функция принимает значение f(x*)=g(y*)=29. Сам оптимальный план x* получим из условия (4.14) теоремы 6. Так как y*=(5;2) имеет две положительных компоненты, то соответствующие им ограничения прямой задачи (4.16) на оптимальном плане x*=(x*1, x*2, x*3, x*4) обращаются в равенства:
При этом x*1=0 и x*4=0, так как первое и четвёртое ограничения системы (4.17) на плане y* обращаются в строгие неравенства. Система уравнений
имеет решение х*2 =18/7, х*3 =1/7. Следовательно, оптимальный план исходной задачи х* = (0; 18/7; 1/7; 0); на нём целевая функция принимает значение f(x*)= Решим теперь задачу (4.17) симплекс-методом. Для этого запишем её в канонической форме, введя дополнительные переменные g (y)=3y1+7y2 →max,
Составим с.-т.: Симплекс – таблица 3.1
Симплекс – таблица 3.2
Второй опорный план y2=( Третий опорный план у3 = (5; 2; 13; 0; 0; 12) является оптимальным, коэффициенты y* = (5;2), max g(y) = g(y*) = 29. Симплекс – таблица 3.3
Оптимальный план х* задачи (4.15)–(4.16) определим, используя последнюю с.-т. 3.3. Воспользуемся формулой для вычисления относительных оценок через оптимальный план двойственной задачи, вытекающей из теоремы 6:
При этом, если y*j — базисная переменная, т.е. y*j > 0, то
Условия (4.20) примут вид: Имеем
|




 можно записать в виде:
можно записать в виде: , (4.3)
, (4.3) ,
,  , …,
, …,  — столбцы матрицы
— столбцы матрицы  системы ограничений,
системы ограничений,  — столбец свободных членов системы.
— столбец свободных членов системы. , тогда
, тогда  допустимых планов задачи (2.8) непусто
допустимых планов задачи (2.8) непусто  и задано в виде системы (4.3). Точка
и задано в виде системы (4.3). Точка  является вершиной многоугольника тогда и только тогда, когда
является вершиной многоугольника тогда и только тогда, когда 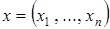 — опорное решение (план) системы
— опорное решение (план) системы  , вплоть до получения оптимального (или выяснения неразрешимости задачи). При этом используют следующие теоремы:
, вплоть до получения оптимального (или выяснения неразрешимости задачи). При этом используют следующие теоремы: является оптимальным планом задачи (2.8), если относительные оценки
является оптимальным планом задачи (2.8), если относительные оценки
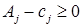
 . (4.4)
. (4.4) называют относительной оценкой замещения переменной
называют относительной оценкой замещения переменной 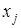 ;
;  — вектор коэффициентов целевой функции
— вектор коэффициентов целевой функции  при базисных переменных
при базисных переменных  ,
,  , …,
, …,  т.е.
т.е. 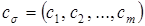 ;
;  — столбец матрицы ограничений
— столбец матрицы ограничений  — коэффициент при переменной
— коэффициент при переменной 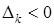 для некоторого номера
для некоторого номера 
 и среди чисел
и среди чисел 
 — элементов столбца
— элементов столбца  — нет положительных (т.е. все
— нет положительных (т.е. все  ), то целевая функция задачи (2.8) не ограничена на множестве её планов.
), то целевая функция задачи (2.8) не ограничена на множестве её планов. задачи (2.8) невырожден и некоторое
задачи (2.8) невырожден и некоторое  такой, что
такой, что  .
. , …,
, …,  по следующей схеме (схема 1):
по следующей схеме (схема 1): , соответствующий отрицательному значению
, соответствующий отрицательному значению  ,
,  ; переменная
; переменная  будет включена в число базисных переменных;
будет включена в число базисных переменных; ,
, таким, что
таким, что  (по множеству
(по множеству  ); переменная
); переменная 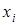 должна быть исключена из числа базисных переменных.
должна быть исключена из числа базисных переменных. ,
,  , …,
, …,  — базисные столбцы, и система
— базисные столбцы, и система  ,
, 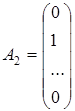 , …,
, …,  ,
, 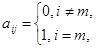 ,
,  .
.
 ,
,  , …,
, …,  и вектор
и вектор  из коэффициентов целевой функции
из коэффициентов целевой функции  при базисных переменных, вверху — небазисные переменные
при базисных переменных, вверху — небазисные переменные  ,
,  , …,
, …,  ; соответствующие этим переменным коэффициенты целевой функции
; соответствующие этим переменным коэффициенты целевой функции  ,
, 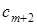 , …,
, …,  и столбцы
и столбцы  ,
, 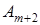 , …,
, …,  матрицы ограничений
матрицы ограничений  », в которой записаны значения относительных оценок небазисных переменных, вычисленные по формуле (4.4), и значение целевой функции
», в которой записаны значения относительных оценок небазисных переменных, вычисленные по формуле (4.4), и значение целевой функции  , вычисленное на первом опорном плане
, вычисленное на первом опорном плане  .
.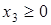 ,
, 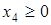 ,
, 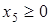 и заменив неравенства равенствами:
и заменив неравенства равенствами: ,
, (4.5)
(4.5) b, (4.10)
b, (4.10) cТ, (4.11)
cТ, (4.11) Rn ; y, b
Rn ; y, b  ), j =(
), j =(  ).
).


 (4.14)
(4.14)
 (
(  ),
), , то y*i=0 (
, то y*i=0 (  то x*j=0
то x*j=0  (4.16)
(4.16) xj
xj 
 .
.
 (4.17)
(4.17)

 → C (5;2).
→ C (5;2). (4.18)
(4.18)
 g(y*).
g(y*).


 :
:

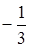





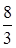

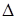 . Второй столбец — разрешающий, вторая строка — разрешающая.
. Второй столбец — разрешающий, вторая строка — разрешающая.





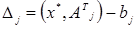
 . (4.20)
. (4.20) , иначе
, иначе  находится в
находится в  -строке табл. 3.3. Матрица ограничений задачи (4.19) содержит четыре единичных столбца A3, A4, A5, A6, поэтому
-строке табл. 3.3. Матрица ограничений задачи (4.19) содержит четыре единичных столбца A3, A4, A5, A6, поэтому ,
,

 ,
,