 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| РЕШЕНИЕ ЛОСУ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ЗАНЯТИЕ 9
Пример 1.Решить систему дифференциальных уравнений
Найти частные решения, удовлетворяющие начальным условиям: а) □ Найдем общее решение данной однородной системы, используя алгоритм 8.3. 1. Матрица коэффициентов системы
Характеристическое уравнение: 2. Решаем квадратное уравнение: 3. По очереди подставляем найденные собственные числа Первому числу
Эта система имеет бесконечное число решений, так как в уравнениях коэффициенты при одинаковых неизвестных пропорциональны. Чтобы построить нетривиальное решение, воспользуемся первым уравнением системы, которое перепишем в виде Второму числу
По аналогии с первым случаем полагаем 4. Фундаментальная система решений линейной однородной системы состоит из двух вектор-функций
или Ответ можно записать и в скалярной форме:
где Завершим выполнение задания решением двух задач Коши, т.е. нахождением таких частных решений, которые удовлетворяют заданным начальным условиям. а) Начальные условия:
В формулах (3) заменим б) Начальные условия:
Подставим эти числа в (3). Решение задачи Коши имеет вид: Пример 2.Решить систему дифференциальных уравнений
□ Используем алгоритм 3. 1. Матрица
Характеристическое уравнение: 2. Решаем квадратное уравнение и находим корни: 3. Найдем собственный вектор, соответствующий собственному числу
Воспользуемся первым уравнением системы, которое перепишем в виде Комплекснозначное частное решение системы имеет вид: Эйлера
По формулам (8.46) 4. Вектор-функции
где
Пример 3.Решить систему дифференциальных уравнений
□ Используем алгоритм 3. 1. Матрица
Характеристическое уравнение:
2. Решаем квадратное уравнение и находим корни:
Как видим, число свободных переменных равно единице. Значит, число линейно независимых собственных векторов Решим пример сведением системы к дифференциальному уравнению. Из первого уравнения системы выразим
Исключим 1. Составим характеристическое уравнение: 2. Характеристические уравнения для исходной системы и полученного дифференциального уравнения совпали. Поэтому сразу запишем корень 3. Этому корню соответствует два частных, линейно независимых между собой решения уравнения: 4. Найденные решения образуют фундаментальную систему решений Вернемся к системе. Вторую функцию соотношения
Обратим внимание на тот факт, что при отыскании
|



 (1)
(1) ; б)
; б)  .
. Система имеет вид:
Система имеет вид: (2)
(2)

 Каждый корень − действительное число и имеет кратность, равную единице. Это первый случай корней характеристического уравнения.
Каждый корень − действительное число и имеет кратность, равную единице. Это первый случай корней характеристического уравнения. матрицы A в систему (2) и находим собственные векторы.
матрицы A в систему (2) и находим собственные векторы. соответствует система
соответствует система или
или 
 Если принять
Если принять  то из уравнения следует, что
то из уравнения следует, что  Вектор
Вектор  − это собственный вектор матрицы А, соответствующий собственному числу
− это собственный вектор матрицы А, соответствующий собственному числу  или
или 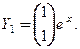
 соответствует система
соответствует система или
или 
 и получаем
и получаем  Значит, собственный вектор матрицы А, соответствующий собственному числу
Значит, собственный вектор матрицы А, соответствующий собственному числу 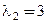 , равен
, равен  . Второе частное решение
. Второе частное решение  или
или 
 , приведенных выше. Составим общее решение:
, приведенных выше. Составим общее решение:

 (3)
(3) − произвольные постоянные.
− произвольные постоянные.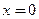 в ответ получаем систему уравнений относительно произвольных постоянных
в ответ получаем систему уравнений относительно произвольных постоянных 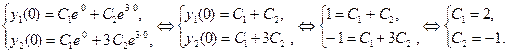
 числами 2 и −1 соответственно и запишем решение задачи Коши:
числами 2 и −1 соответственно и запишем решение задачи Коши: 
 . Аналогично случаю а) составляем и решаем систему уравнений относительно произвольных постоянных
. Аналогично случаю а) составляем и решаем систему уравнений относительно произвольных постоянных 
 Получено решение, называемое тривиальным. Результат закономерный, так как однородная система с постоянными коэффициентами удовлетворяет условиям теоремы существования и единственности решения задачи Коши, Поскольку тривиальное решение удовлетворяет системе и заданным начальным условиям, то согласно теореме (8.6) оно единственное. ■
Получено решение, называемое тривиальным. Результат закономерный, так как однородная система с постоянными коэффициентами удовлетворяет условиям теоремы существования и единственности решения задачи Коши, Поскольку тривиальное решение удовлетворяет системе и заданным начальным условиям, то согласно теореме (8.6) оно единственное. ■
 Система (8.42) имеет вид:
Система (8.42) имеет вид: (4)
(4)

 Корни образуют пару комплексно-сопряженных чисел, кратности корней − единица. Это соответствует второму случаю корней характеристического уравнения.
Корни образуют пару комплексно-сопряженных чисел, кратности корней − единица. Это соответствует второму случаю корней характеристического уравнения. . Для этого подставим
. Для этого подставим  в систему (4):
в систему (4):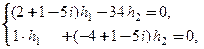 или
или 
 Если принять
Если принять  то из уравнения следует, что
то из уравнения следует, что  Заметим, что найденная пара чисел удовлетворяет и второму уравнению системы. Вектор
Заметим, что найденная пара чисел удовлетворяет и второму уравнению системы. Вектор  − это собственный вектор матрицы А, соответствующий собственному числу
− это собственный вектор матрицы А, соответствующий собственному числу  .
. или
или  Преобразуем полученное выражение:
Преобразуем полученное выражение:  По формуле
По формуле . Тогда
. Тогда



 образуют фундаментальную систему решений. Тогда
образуют фундаментальную систему решений. Тогда
 ■
■
 Система (8.42) имеет вид:
Система (8.42) имеет вид: (5)
(5)

 Отсюда следует, что число
Отсюда следует, что число  является корнем кратности
является корнем кратности 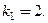 Это 3-й случай для корней характеристического уравнения. Ищем собственный вектор H из системы (5), в которую подставим
Это 3-й случай для корней характеристического уравнения. Ищем собственный вектор H из системы (5), в которую подставим 

 также равно единице. Так как
также равно единице. Так как  то алгоритм 3 не подходит (не позволяет построить ФСР).
то алгоритм 3 не подходит (не позволяет построить ФСР).

 из второго уравнения системы:
из второго уравнения системы:  Упростим уравнение:
Упростим уравнение: 
 Получено линейное однородное уравнение 2-го порядка с постоянными коэффициентами. Используем алгоритм 1.
Получено линейное однородное уравнение 2-го порядка с постоянными коэффициентами. Используем алгоритм 1. .
. и его кратность
и его кратность 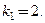
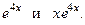
 Следовательно, общее решение имеет вид:
Следовательно, общее решение имеет вид:  , или
, или  .
. , входящую в систему, найдем из
, входящую в систему, найдем из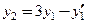 , в которое подставим полученную функцию
, в которое подставим полученную функцию 
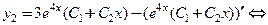


 ■
■