 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ИССЛЕДОВАНИЕ ЗНАКОПОЛОЖИТЕЛЬНЫХ РЯДОВ
ЗАНЯТИЕ 10 Схема исследования сходимости рядов
Схема содержит все изложенные выше признаки сходимости и расходимости знакоположительных рядов. Направления перемещения по схеме указаны стрелками. Признаки разбиты на три группы (уровня). В первую группу включены предельные признаки Даламбера и Коши, во вторую − необходимый признак сходимости, в третью − признаки сравнения, интегральный признак Коши и другие признаки. Под термином «другие признаки» подразумеваются признаки, не рассматриваемые в данной работе, в частности, признаки Даламбера и Коши в непредельной форме, признаки Раабе, Гаусса, являющиеся более глубокими, но и более сложными средствами исследования рядов. При применении схемы желательно учитывать следующие рекомендации. Если общий элемент знакоположительного ряда содержит факториал Если общий элемент является показательно-степенным выражением вида При применении предельных признаков нужно использовать все средства вычисления пределов: правила предельных переходов, замечательные пределы, таблицу эквивалентных функций, правила Лопиталя (см. разделы 2 и 3). Значения При использовании предельных признаков Даламбера и Коши необходимые вычисления можно выполнять по шагам в соответствии с алгоритмами, приведенными ниже.
Алгоритм применения предельного признака Даламбера
Написать общий элемент ряда Написать Составить частное Найти Сделать вывод о сходимости или расходимости ряда при
Алгоритм применения предельного признака КОШИ
Написать общий элемент ряда Составить выражение Найти Сделать вывод о сходимости или расходимости ряда при
З а м е ч а н и е. При использовании предельного признака Коши полезно знать, что
Этот предел связан с раскрытием неопределенности вида
Пример 1. Исследовать на сходимость ряд □ Первый элемент ряда равен нулю, остальные − положительные числа. Применим предельный признак Даламбера. Выполним вычисления по шагам в соответствии с алгоритмом. 1. 2. 3. 4. 5. Сравниваем найденное предельное значение Пример 2. Исследовать на сходимость ряд □ Выбираем признак Даламбера, так как общий элемент ряда содержит факториал 1. 2. 3. 4. 5. Пример 3. Исследовать на сходимость ряд □ Применим признак Даламбера. 1. 2. 3. 4. 5. Вывод: признак Даламбера не дает ответа. Нужно продолжить исследование.
Применим предельный признак Коши, пользуясь алгоритмом. 1. 2. 3. 4. Пример 4. Исследовать на сходимость ряд □ Общий элемент ряда является показательно-степенной функцией, поэтому применим предельный признак Коши. 1. 2. 3. 4. Пример 5. Исследовать на сходимость ряд □ Общий элемент заданного ряда снова является показательно-степенной функцией, поэтому применим предельный признак Коши. 1. 2. 3. 4. В соответствии со схемой исследования опустимся в ней на уровень ниже и проверим, выполнен ли необходимый признак сходимости. Для этого найдем предел общего элемента ряда:
|



 с неотрицательными элементами
с неотрицательными элементами



 или произведение переменного числа сомножителей (например,
или произведение переменного числа сомножителей (например,  ), то целесообразно применять предельный признак Даламбера.
), то целесообразно применять предельный признак Даламбера. , то следует применять предельный признак Коши.
, то следует применять предельный признак Коши. , найденные по предельным признакам Даламбера и Коши, равны, если соответствующие пределы существуют. Если по предельному признаку Даламбера нельзя найти значение
, найденные по предельным признакам Даламбера и Коши, равны, если соответствующие пределы существуют. Если по предельному признаку Даламбера нельзя найти значение 

 и упростить.
и упростить.
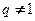 , или о необходимости продолжения исследования (если
, или о необходимости продолжения исследования (если  ).
). и упростить.
и упростить.
 (1)
(1) . В литературе [ ] его относят к числу замечательных пределов.
. В литературе [ ] его относят к числу замечательных пределов.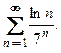
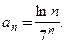



 с числом 1:
с числом 1:  . Приходим к заключению, что ряд сходится. ■
. Приходим к заключению, что ряд сходится. ■
 Вычисления выполняем по алгоритму.
Вычисления выполняем по алгоритму.

 Здесь использовано свойство факториала:
Здесь использовано свойство факториала: 


 Ряд сходится. ■
Ряд сходится. ■



 не существует, так как частичные подпоследовательности последовательности
не существует, так как частичные подпоследовательности последовательности  с четными и нечетными индексами состоят из чисел
с четными и нечетными индексами состоят из чисел  и 1 и имеют разные пределы, равные
и 1 и имеют разные пределы, равные 
 Поскольку элементы последовательности
Поскольку элементы последовательности  принимают только два значения: 1 − при нечетных значениях индекса
принимают только два значения: 1 − при нечетных значениях индекса  и 3 − при четных, то пределы соответствующих подпоследовательностей равны
и 3 − при четных, то пределы соответствующих подпоследовательностей равны 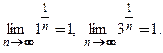 Как видим, они имеют общий предел, равный единице. Значит,
Как видим, они имеют общий предел, равный единице. Значит,  Тогда
Тогда 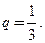
 Исходный ряд сходится. ■
Исходный ряд сходится. ■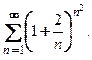



 Ряд расходится. ■
Ряд расходится. ■



 Признак Коши ответа не дает. Требуется дополнительное исследование.
Признак Коши ответа не дает. Требуется дополнительное исследование.
 Общий элемент не стремится к нулю, следовательно, ряд расходится.■
Общий элемент не стремится к нулю, следовательно, ряд расходится.■