 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ФСР однородного ЛДУ с постоянными коэффициентами в случае, когда характеристическое ур-ие имеет кратные корни 12
Метод вариации произвольных постоянных для неоднородного ЛДУ порядка n Пусть дано ур-ие:
и пусть Ищем Где
Наложим на
Положим Тогда Тогда Вычислим: Для определения Главный определитель системы: W(x)=W[ Т.к.
ФСР однородного ЛДУ с постоянными коэффициентами в случае простых корней характеристического ур-ия(действительных или комплексных)
L(V)- множ-во всех линейных операторов действующих в V(линейное пр-во). Опред.: Для
Поставим в соответствие ур-ию (13) и оператору L многочлен от переменной t вида: Ясно что L(D)=l(D) (14) Опред.:Многочлен Теорема:Функция Док-во: Т.е. Теорема(ФСР ЛДУ):Пусть
Док-во:Т.к. а)Действительный случай: (17)
1)
2)
Re Если f(x)=u(x)+iv(x) – решение (17), то u(x),v(x) - решение (17)
б)Общий случай:Пусть n=k+2m, ФСР имеет вид:
Общее решение:
ФСР однородного ЛДУ с постоянными коэффициентами в случае, когда характеристическое ур-ие имеет кратные корни
Опред.:Говорят что число Пусть
Рассмотрим
Теорема8:Пусть Док-во: Т.к.
Лемма5:Для Система функций: линейно независима на Теорема9:Пусть различные
Док-во: Т.к. решения ур-ия (13) Согласно Лемме 5 эти функции линейно независимы на
где А)Действительный случай:
1)Пусть
2)
Комплексные функции теорема 8:
По теореме: Re Im
Общий случай: Пусть
Тогда общее решение ур-ия (17) имеет вид:
где
12 |




 , C1-Cn-произв. постоянные – общее решение соответсвующего однородного ур-ия L[y]=0
, C1-Cn-произв. постоянные – общее решение соответсвующего однородного ур-ия L[y]=0
 непрерывно дифф-мы на I, подлежащее определению
непрерывно дифф-мы на I, подлежащее определению =1…n
=1…n  L[
L[  ;
; дополнительные ограничения:
дополнительные ограничения:




 получим систему из n уравнений:
получим систему из n уравнений:
 - определитель Вронского
- определитель Вронского 
 - линейно независимые решения ур-ия (9), то по теореме 3: для
- линейно независимые решения ур-ия (9), то по теореме 3: для  . Следовательно система (13) имеет единственное решение на промежутке I, которое находится по теореме Крамера:
. Следовательно система (13) имеет единственное решение на промежутке I, которое находится по теореме Крамера: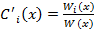 , где
, где  получаем из W(x) заменой i-го столбца на столбец
получаем из W(x) заменой i-го столбца на столбец




 Все решения ур-ия (13) определены на
Все решения ур-ия (13) определены на 
 A+B
A+B  ;
;
 (
( 

 (15)
(15) называется характеристическим многочленом однородного ЛДУ (13) и оператора (14)
называется характеристическим многочленом однородного ЛДУ (13) и оператора (14) , где
, где  является решением ур-ия (13) т. и т.т. когда
является решением ур-ия (13) т. и т.т. когда  - есть корень характеристического многочлена (15)
- есть корень характеристического многочлена (15)

 корни характеристического ур-ия (15) попарно различны, тогда функции
корни характеристического ур-ия (15) попарно различны, тогда функции  образуют ФСР ур-ия (13) и общее решение имеет вид:
образуют ФСР ур-ия (13) и общее решение имеет вид: , где
, где  - произвольные комплексные постонные.
- произвольные комплексные постонные.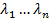 – корни ур-ия (15) то по теореме 6, экспоненты
– корни ур-ия (15) то по теореме 6, экспоненты  , то функции
, то функции  …
…  - линейно независимы. Их n и опр. линейно независимы след-но образуют ФСР.
- линейно независимы. Их n и опр. линейно независимы след-но образуют ФСР.



 ,
, 



 Im(
Im( 
 |à решения ур-ия (17) линейно
|à решения ур-ия (17) линейно | àнезависимы
| àнезависимы - ращличные действительные корни характеристического ур-ия,
- ращличные действительные корни характеристического ур-ия,  - различные корни характеристич. ур-ия
- различные корни характеристич. ур-ия


 ,
,  – действительные произвольные корни
– действительные произвольные корни кратности k,если
кратности k,если  где
где  многочлен степени(n-k),
многочлен степени(n-k),  .
.
 ;
;

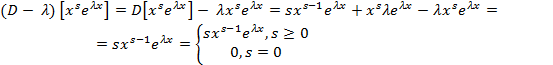


 тогда функции
тогда функции  являются решением ур-ия (13).
являются решением ур-ия (13).
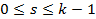

 Функция
Функция  - решение ур-ия (13)
- решение ур-ия (13) различных чисел
различных чисел 


 – корни характеристического многочлена
– корни характеристического многочлена  – соответственно. Тогда общее решение ур-ия (13) имеет вид:
– соответственно. Тогда общее решение ур-ия (13) имеет вид: , где
, где  – многочлен степени
– многочлен степени  с произвольными комплексными коэффициентами
с произвольными комплексными коэффициентами j=1…s;
j=1…s; 
 - корень характеристического многочлена
- корень характеристического многочлена 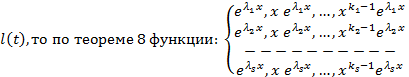
 их
их  Следовательно построенная система – ФСР ур-ия (13) и
Следовательно построенная система – ФСР ур-ия (13) и
 –произвольная постоянная.
–произвольная постоянная.


 (
( 
 – действительные решения
– действительные решения
 ;
; 

 – решение ур-ия (17)
– решение ур-ия (17) 
 – решения ур-ия (17)
– решения ур-ия (17)
 действительные корни
действительные корни  соответсвенно,
соответсвенно,  – комплексные корни ур-ия (15) кратности
– комплексные корни ур-ия (15) кратности  соответственно
соответственно

 -многочлен степени
-многочлен степени  –многочлены степени
–многочлены степени  с произвольными действительными коэффициентами.
с произвольными действительными коэффициентами.