 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Базові поняття алгебри логіки
Основними об’єктами алгебри логіки є елементарні висловлювання – висловлювання, про які однозначно можна сказати, що вони істинні або хибні. Кожне елементарне висловлювання алгебри логіки повинно задовольняти двом вимогам: 1) Закон виключення третього. Висловлювання може бути або істинним, або хибним. Третього не дано. 2) Закон протиріччя. Висловлювання не може одночасно бути і істинним, і хибним. Функцією алгебри логіки (логічною функцією) Серед операцій алгебри логіки визначають наступні:
Таблиця істинності операцій алгебри логіки.
Пріоритетність логічних операцій (порядок їхнього виконання у формулі при відсутності дужок): 1. операція заперечення; 2. операція кон’юнкції; 3. операція диз’юнкції; 4. усі решта введених операцій зліва направо в порядку входження у формулу.
Розглянемо основні закони операцій алгебри логіки, застосовні до трьох змінних 1.Закони комутативності 2.Закони асоціативності 3.Дистрибутивний закон для кон'юнкції по відношенню до диз'юнкції 4.Дистрибутивний закон для диз'юнкції по відношенню до кон'юнкції 5.Закон подвійного заперечення 6.Закони де-Моргана (закони двоїстості) 7.Закони ідемпотентності 8.Закони поглинання 9.Операції з константами 0 та 1.
10.Закон виключення третього 11.Закон суперечливості (протиріччя) Справедливість цих законів еквівалентності може бути перевірена за допомогою таблиць істинності. Алгебраїчна структура У алгебрі Жегалкіна виконуються закони: 1. Закони комутативності 2. Закони асоціативності 3. Дистрибутивний закон для кон'юнкції по відношенню до додавання по модулю два 4. Закони ідемпотентності для кон'юнкції 5. Закон поглинання (зведення подібних членів при додаванні за модулем два 6. Операції з константами 0 та 1.
Наведемо еквівалентності, що дозволяють перетворити будь-яку формулу алгебри логіки у формулу алгебри Жегалкіна чи відповідно у формулу алгебри Буля:
Наведемо декілька прикладів розв'язування задач з алгебри логіки.
Приклад 1. Побудувати таблиці істинності формули Розв’язування. На підставі таблиці істинності для бінарних логічних операцій побудуємо відповідні таблицю істинності для заданої формули Таблиця істинності формули
Приклад 2. Мінімізувати формулу алгебри логіки, що задана в попередньому завданні. Розв’язування. Скористаємося побудованою вище таблицею істинності формули
Далі проведемо неповне склеювання елементарних кон’юнкцій між собою
Подальший аналіз одержаного виразу свідчить про мінімальний рівень складності виразу
Приклад 3. Побудувати еквівалентну формулу у алгебрі Жегалкіна для формули, що задана в попередньому завданні. Розв’язування. Скористаємося наступними співвідношеннями між операціями алгебри логіки:
4. Основні елементи теорії графів.
Предметом перших задач в теорії графів були конфігурації, які можна було зобразити у вигляді точок та ліній, що їх з’єднують. При чому не суттєво, прямі ці лінії чи ні, довгі вони чи короткі, суттєво лише те, що вони з’єднують дві вказані точки. Граф – це множина точок Дамо означення деяких основних понять теорії графів. Дуга Вершини є інцидентними дузі, якщо дана дуга їх з’єднує. Дві вершини Дві дуги Вершина, не інцидентна жодному ребру, називається ізольованою вершиною. Вершина, що є початковою вершиною для деяких дуг, але не є кінцевою вершиною жодної дуги, називається вершиною виходу. Вершина, що є кінцевою вершиною для деяких дуг, але не є початковою вершиною жодної дуги, називається вершиною входу. Кількість дуг, що виходить з даної вершини називається напівстепенем виходу. Кількість дуг, що входить у дану вершину називається напівстепенем входу. Сума напівстепеня входу та напівстепеня виходу називається степенем вершини. Дуга, початкова та кінцева вершини якої співпадають, називається петлею. Граф, що складається лише з ізольованих вершин, називається нуль-графом. Граф, ребрами якого являються всі можливі пари для двох різних його вершин Граф називається неорієнтованим, якщо кожне ребро його не орієнтоване, і орієнтованим, якщо орієнтовані всі його ребра. Деколи у графі деякі ребра є орієнтованими, а інші – ні, тоді такий граф називають графом змішаного типу. Шляхом у графі називають таку послідовність його дуг, у якій кінцева вершина кожної попередньої дуги є одночасно початковою вершиною наступної дуги. Довжиною шляху називають кількість дуг, що його утворює. Контуром у графі називають замкнений шлях, тобто шлях, у якому початкова та кінцева вершина співпадають. Довжиною контура називають кількість дуг, що його утворює. Шлях називається елементарним, якщо всі вершини, які він містить, є різними. Контур називається елементарним, якщо всі вершини, які він містить, за винятком початкової та кінцевої, є різними. Шлях називається простим, якщо всі дуги, які він містить, є різними. Контур називається простим, якщо всі дуги, які він містить, є різними. Граф, у якому для будь-якої пари його вершин існує шлях, що їх з'єднує, називається зв’язним. Зваженим називається граф, у якого кожній його дузі поставлено у відповідність певне невід’ємне число, що називається вагою дуги. Вагою (довжиною) шляху називається кількість (або сума всіх ваг) дуг, що його утворюють. Підграфом заданого графа G називається граф, в який входить лише частина вершин графа G з інцидентними дугами. Частковим графом графу G називається граф, що містить частину дуг основного графа і всі вершини, що належать основному графу G. Зауваження: для неорієнтованого графа в усіх визначеннях замість поняття дуга використовують поняття ребро, шлях – називають ланцюгом чи маршрутом, а контур – циклом.
Способи задання графа
2. Граф можна задати через відображення, визначивши множину його вершин та множину відображень кожної із вершин:
3. Граф можна задати через К-список (підмножину декартового добутку множини вершин графа самої на себе).
4. Найбільш математичним способом задання графа вважають його задання через матрицю суміжності чи матрицю інцидентності. Матрицею суміжності, відповідною до заданного графа, називають квадратну матрицю, розмірність якої дорівнює кількості його вершин, а елементами якої є числа 0 або 1. Причому елемент матриці Матрицею інцидентності, відповідної до заданого графа, називають прямокутну матрицю, кількість рядків якої дорівнює кількості вершин графа, а кількість стовпців – кількості його дуг. Елементами матриці є числа 0, 1 і -1, причому елемент матриці Для того, щоб дати характеристику графа (незалежно від способу його задання) необхідно вказати: – множину вершин даного графа; – ізольовані вершини, вершини входу та виходу (якщо вони існують); – тип графа (щодо орієнтованості); – вказати чи заданий граф є повним; – вказати чи заданий граф є зв’язним;
Наведемо деякі основні задачі в теорії графів.
1.Знаходження найкоротшого шляху у графі. Нехай у заданому графі необхідно знайти найкоротший шлях із усіх можливих, що з’єднують вершину Спершу вершині
2. Знаходження оптимального шляху у зваженому графі (шляху мінімальної ваги). Нехай у заданому зваженому графі необхідно знайти шлях найменшої ваги з усіх можливих, що з’єднують вершину Спершу проводимо початкову індексацію вершин: вершині Якщо індекс вершини
3.Знаходження числа шляхів або контурів заданої довжини. Нехай необхідно знайти кількість шляхів довжини k, що з’єднують вершини У випадку, коли необхідно знайти кількість контурів, діємо аналогічним чином, враховуючи означення контура, – результат буде міститися на головній діагоналі результуючої матриці. Сума діагональних елементів становить число всіх контурів потрібної довжини у заданому графі.
Наведемо декілька прикладів розв'язування задач із теорії графів. Приклад 1. Охарактеризувати граф, заданий матрицею суміжності
Розв’язування. Скористаємося планом характеристики графа, що поданий у теоретичній частині. 1. Множина вершин даного графа 2. Вершина h є ізольованою, оскільки в матриці суміжності цій вершині відповідають нульовий рядок і стовпець. Вершинами входу є вершини 3. Оскільки матриця суміжності несиметрична – граф є графом змішаного типу. Існують строго напрямлені дуги такі як 4. Оскільки у графі є ізольована вершина, то граф не є повним і не є зв’язним.
Приклад 2. Граф, що заданий у попередньому завданні записати через відповідні множини відображень. Розв’язування. Множина вершин даного графа Запишемо множину відображень для кожної вершини графа:
Приклад 3. Знайти кількість контурів довжини 3 з вершини a та кількість шляхів довжини 2, що з’єднують вершини c та b у підграфі графа, який заданий у попередньому завданні з вершинами Розв’язування. Для знаходження кількості шляхів довжини 2, що з’єднують вершини c та b необхідно матрицю суміжності
Квадрат матриці суміжності заданого графа є матрицею вигляду
Кількість шляхів довжини 2, що з’єднують вершини c та b визначає елемент Для визначення кількості контурів довжини 3 з вершини a необхідно знайти елемент Завдання для самостійної роботи
Завдання з розділу „Теорія множин” 1. Дано
2.Задано множини:
Знайти результат виконання операцій над множинами.
3. Задано множини:
4. Використовуючи операції над множинами, розв'язати задачу:
4.1. Кожен учень у класі вивчає англійську або французьку мову. Тільки англійську мову вивчають 7 учнів, тільки французьку – 5, а 16 учнів вивчають обидві мови. Скільки учнів у класі? 4.2. У класі 30 учнів. Кожен із них займається футболом або хокеєм. Третина учнів класу займається тільки хокеєм, а 5 учнів і хокеєм, і футболом. Скільки учнів займаються футболом? 4.3. У класі 35 учнів. Кожен учень у класі вивчає англійську або німецьку мову. Англійську мову вивчають 17 учнів, а німецьку – 25. Скільки учнів у класі вивчають і англійську, і німецьку мови? 4.4. У класі 20 учнів. Кожен із них відвідує факультативні заняття з математики, фізики чи хімії. 5 учнів класу відвідують лише математичний факультатив, фізикою займаються 8 учнів, а хімією –12. Скільки учнів класу відвідують більше, ніж один факультатив? 4.5. У класі 40 учнів. Кожен із них займається футболом чи хокеєм. Половина учнів класу займається тільки хокеєм, а 10 учнів – тільки футболом. Скільки учнів класу займаються і хокеєм, і футболом? 4.6. У групі з 20 дітей половина захоплюється малюванням, а інші музикою або танцями. Тільки музикою захоплюється 4 дітей, 3 дітей захоплюються і музикою, і танцями. Скільки дітей захоплюється танцями? 4.7. У класі 33 учні. На домашнє завдання слід було виконати 5 вправ. Усі учні виконали хоча б 3 вправи. 10 учнів виконали домашнє завдання повністю. Скільки учнів класу виконали лише 4 вправи? 4.8. На домашнє завдання слід було виконати 2 вправи. 10 учнів виконали першу вправу, 12 учнів зробили лише друге завдання. 2 учнів виконали домашнє задання повністю. Скільки учнів у класі? 4.9. У дитячому садку вивчали вірші та приказки. 10 дітей вивчили вірш, а 15 вивчили приказку, 5 дітей вивчили і вірш, і приказку. Скільки дітей у групі дитсадка? 4.10. У класі 20 учнів. На домашнє завдання потрібно було вивчити вірша чи прислів’я. Половина дітей вивчили вірш, а 7 вивчили і вірш, і прислів’я. Скільки дітей вивчили прислів’я? 4.11. Кожен учень у класі вивчає англійську або французьку мову. Лише англійську мову вивчають 7 учнів, лише французьку – 5, а 16 вивчають обидві мови. Скільки учнів у класі? 4.12. У класі 30 учнів. Кожен з них займається футболом чи хокеєм. Третина учнів класу займається тільки хокеєм, а 5 учнів і хокеєм, і футболом. Скільки учнів займаються футболом? 4.13. У класі 35 учнів. Кожен учень у класі вивчає англійську або німецьку мову. Англійську мову вивчають 17 учнів, а німецьку – 25. Скільки учнів у класі вивчають і англійську, і німецьку мови? 4.14. У класі 20 учнів. Кожен з них відвідує факультативні заняття з математики, фізики чи хімії. 5 учнів класу відвідують лише математичний факультатив, фізикою займаються 8 учнів, а хімією –12. Скільки учнів класу відвідують більше, ніж один факультатив? 4.15. У класі 40 учнів. Кожен з них займається футболом чи хокеєм. Половина учнів класу займається тільки хокеєм, а 10 учнів – тільки футболом. Скільки учнів класу займаються і хокеєм, і футболом? 4.16. У групі з 20 дітей половина захоплюється малюванням, а інші музикою або танцями. Тільки музикою захоплюється 4 дітей, 3 дітей захоплюються і музикою, і танцями. Скільки дітей захоплюється танцями? 4.17. У класі 33 учні. На домашнє завдання слід було виконати 5 вправ. Усі учні виконали хоча б 3 вправи. 10 учнів виконали домашнє завдання повністю. Скільки учнів класу виконали лише 4 вправи? 4.18. На домашнє завдання слід було виконати 2 вправи. 10 учнів виконали першу вправу, 12 учнів зробили лише друге завдання. 2 учнів виконали домашнє завдання повністю. Скільки учнів у класі? 4.19. У дитячому садку вивчали вірші та приказки. 10 дітей вивчили вірш, а 15 вивчили приказку, 5 дітей вивчили і вірш, і приказку. Скільки дітей у групі? 4.20. У класі 20 учнів. На домашнє завдання потрібно було вивчити вірша чи прислів’я. Половина дітей вивчили вірш, а 7 вивчили і вірш, і прислів’я. Скільки дітей вивчили прислів’я? 4.21. Кожен учень у класі вивчає англійську або французьку мову. Лише англійську мову вивчають 7 учнів, лише французьку – 5, а 16 вивчають обидві мови. Скільки учнів у класі? 4.22. У класі 30 учнів. Кожен з них займається футболом чи хокеєм. Третина учнів класу займається тільки хокеєм, а 5 учнів і хокеєм, і футболом. Скільки учнів займаються футболом? 4.23. У класі 35 учнів. Кожен учень у класі вивчає англійську або німецьку мову. Англійську мову вивчають 17 учнів, а німецьку – 25. Скільки учнів у класі вивчають і англійську, і німецьку мови? 4.24. У класі 20 учнів. Кожен з них відвідує факультативні заняття з математики, фізики чи хімії. 5 учнів класу відвідують лише математичний факультатив, фізикою займаються 8 учнів, а хімією – 12. Скільки учнів класу відвідують більше, ніж один факультатив? 4.25. У класі 40 учнів. Кожен з них займається футболом чи хокеєм. Половина учнів класу займається тільки хокеєм, а 10 учнів – тільки футболом. Скільки учнів класу займаються і хокеєм, і футболом? 4.26. У групі з 20 дітей половина захоплюється малюванням, а інші музикою або танцями. Тільки музикою захоплюється 4 дітей, 3 дітей захоплюються і музикою, і танцями. Скільки дітей захоплюється танцями? 4.27. У класі 33 учні. На домашнє завдання слід було виконати 5 вправ. Усі учні виконали хоча б 3 вправи. 10 учнів виконали домашнє завдання повністю. Скільки учнів класу виконали лише 4 вправи? 4.28. На домашнє завдання слід було виконати 2 вправи. 10 учнів виконали першу вправу, 12 учнів зробили лише друге завдання. 2 учнів виконали домашнє завдання повністю. Скільки учнів у класі? 4.29. У дитячому садку вивчали вірші та приказки. 10 дітей вивчили вірш, а 15 вивчили приказку, 5 дітей вивчили і вірш, і приказку. Скільки дітей у групі? 4.30. У класі 20 учнів. На домашнє завдання потрібно було вивчити вірша чи прислів’я. Половина дітей вивчили вірш, а 7 вивчили і вірш, і прислів’я. Скільки дітей вивчили прислів’я? Завдання з розділу „Комбінаторика”
5. Розв’язати задачу та пояснити хід розв’язання. 5.1. Скільки різних послідовностей можна утворити з 6-ти одиниць та 10-ти нулів? 5.2. Скільки різних шестисимвольних кодів можна утворити на множині літер української абетки? 5.3. Скількома різними способами можна поставити в два ряди семеро осіб для виконання їх групового портрету? 5.4. У повному комплекті гри в доміно – 28 кісточок. Скільки кісточок буде мати повний комплект дитячого доміно, якщо замість цифр використати 9 різних малюнків? 5.5. Скількома способами можна розселити 12 студентів у 4 тримісні кімнати гуртожитку? 5.6. Скількома способами можна розділити групу з 24 студентів на дві рівні підгрупи для здачі модульного контролю? 5.7. Скількома способами можна розділити групу з 24 студентів на три рівні підгрупи для здачі нормативів з фізкультури? 5.8. Із 19 запитань потрібно скласти екзаменаційні білети, причому в кожен білет вписується лише два запитання. Скільки таких білетів можна скласти? 5.9. Десять нових працівників необхідно розподілити на робочі місця. Існує 6 відділів, причому кожен зі співробітників може працювати у будь-якому відділі. Скількома способами можна зробити призначення? 5.10. У дитячий садок надійшло 5 нових дітей, яких треба розподілити в 7 груп, причому в одну групу не більше однієї дитини. Скільки можливостей розподілу по групах в цьому випадку існує? 5.11. Скільки різних послідовностей можна утворити з 4-ох одиниць та 12-ти нулів? 5.12. Скільки різних семисимвольних кодів можна утворити на множині літер латинської абетки? 5.13. Скількома різними способами можна поставити в два ряди 6 осіб для виконання їх групового портрету? 5.14. У повному комплекті гри в доміно – 28 кісточок. Скільки кісточок буде мати повний комплект дитячого доміно, якщо замість цифр використати 5 різних малюнків? 5.15. Скількома способами можна розселити 12 студентів у 3 чотиримісні кімнати гуртожитку? 5.16. Скількома способами можна розділити групу з 20 студентів на дві рівні підгрупи для здачі модульного контролю? 5.17. Скількома способами можна розділити групу з 21 студентів на три рівні підгрупи для здачі нормативів з фізкультури? 5.18. Із 26 запитань потрібно скласти екзаменаційні білети, причому в кожен білет вписується лише два запитання. Скільки таких білетів можна скласти? 5.19. Десять нових працівників необхідно розподілити на робочі місця. Існує 5 відділів, причому кожен зі співробітників може працювати у будь-якому відділі. Скількома способами можна зробити призначення? 5.20. У дитячий садок надійшло 6 нових дітей, яких треба розділити в 7 груп, причому в одну групу не більше однієї дитини. Скільки можливостей розподілу по групах в цьому випадку існує? 5.21. Скільки різних послідовностей можна утворити з 8-ми одиниць та 8-ми нулів? 5.22. Скількома способами за круглим столом можемо розсадити 10 гостей так, щоб певна пара сиділа поруч? 5.23. Скільки різних п’ятисимвольних кодів можна утворити на множині десяти арабських цифр абетки? 5.24. Скількома різними способами можна поставити в ряд семеро і восьмеро хлопців, щоб дівчата не стояли на груповому портреті поруч? 5.25. Скількома способами можна розселити 9 студентів у 3 тримісні кімнати гуртожитку? 5.26. Скількома способами можна розділити групу з 26 студентів на дві рівні підгрупи для здачі модульного контролю? 5.27. Скількома способами можна розділити групу з 24 студентів на чотири рівні підгрупи для здачі нормативів з фізкультури? 5.28. Скільки різних двійкових чисел можна утворити з 6-ти одиниць та 10-ти нулів, щоб у старшому розряді була одиничка? 5.29. Вісім нових працівників необхідно розподілити на робочі місця. Існує 6 відділів, причому кожен зі співробітників може працювати у будь-якому відділі. Скількома способами можна зробити призначення? 5.30. У дитячий садок надійшло 5 нових дітей, яких треба розділити в 7 груп, причому в одну групу не більше однієї дитини. Скільки можливостей розподілу по групах в цьому випадку існує?
6. Задано множину 6.1. Скільки існує різних перестановок із елементів цієї множини. 6.2. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять число 11. 6.3. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять числа 11 і 13. 6.4. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять число 11 або 13. 6.5. Скільки існує розміщень із елементів цієї множини по 4 елементи, що містять числа 1 і 2 або 17. 6.6. Скільки існує розміщень із елементів цієї множини по 4 елементи, що містять числа 1 і 17. 6.7. Скільки існує різних перестановок із підмножини елементів цієї множини, які мають парні індекси. 6.8. Скільки існує різних перестановок із підмножини елементів цієї множини, які мають непарні індекси. 6.9. Скільки існує різних перестановок із підмножини елементів цієї множини, які мають індекси кратні 3. 6.10. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять число 13. 6.11. Скільки різних намист можна укласти з 10 намистин різного розміру. 6.12. Скількома способами можна вибрати 3 однакові карти з 6.13. Скількома способами можна вибрати 5 послідовно занумерованих карт з колоди 6.14. Скількома способами можна вибрати 5 карт з колоди 6.15. Скількома способами можна вибрати 5 послідовно занумерованих карт однієї масті з колоди 6.16. Скількома способами можна вибрати 5 карт з колоди 6.17. Скількома способами можна приставити дві кісточки одна до одної з набору 28 доміно так, щоб суміжні поля обидвох співпадали. 6.18. Скільки різних намист можна укласти з 20 намистин різного розміру. 6.19. Скількома способами можна вибрати 5 карт з колоди 6.20. Скільки різних намист можна укласти з 10 намистин, серед яких 8 намистин одного типорозміру, а ще дві є дещо більшими.
Задано множину 6.21. Скільки існує різних перестановок із елементів цієї множини. 6.22. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять число 12. 6.23. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять числа 12 і 14. 6.24. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять число 12 або 14. 6.25. Скільки існує розміщень із елементів цієї множини по 4 елементів, що містять числа 2, 4, 16. 6.26. Скільки існує розміщень із елементів цієї множини по 4 елементів, що містять числа 2 і 16. 6.27. Скільки існує різних перестановок із підмножини елементів цієї множини, які мають парні індекси. 6.28. Скільки існує різних перестановок із підмножини елементів цієї множини, які мають непарні індекси. 6.29. Скільки існує різних перестановок із підмножини елементів цієї множини, які мають індекси кратні 3. 6.30. Скільки існує розміщень із елементів цієї множини по 5 елементів, що містять число 14.
7. Виконати завдання. Довести тотожність. 7.1. 7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.10.
Обчислити коефіцієнти многочлена: 7.11. 7.12. 7.13. Обчислити значення коефіцієнта при степені у многочлені: 7.14. 7.15. 7.16. Скільки є членів у вказаному виразі? 7.17. 7.18. 7.19. |



 від
від  змінних
змінних 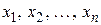 називатимемо функцію, яка приймає значення 0 та 1 (істинне, хибне), і аргументи якої теж можуть приймати значення 0, 1 (істинне, хибне).
називатимемо функцію, яка приймає значення 0 та 1 (істинне, хибне), і аргументи якої теж можуть приймати значення 0, 1 (істинне, хибне). – операція заперечення;
– операція заперечення; (
(  ) – операція кон’юнкції або логічного множення;
) – операція кон’юнкції або логічного множення; – операція диз’юнкції або логічного додавання;
– операція диз’юнкції або логічного додавання; – операція імплікації;
– операція імплікації; – операція еквівалентності або рівнозначності;
– операція еквівалентності або рівнозначності; – операція Шеффера;
– операція Шеффера; – операція Пірса;
– операція Пірса; – операція додавання за модулем два або операція нерівнозначності.
– операція додавання за модулем два або операція нерівнозначності.









 .
.










 називається алгеброю Буля. Алгебра
називається алгеброю Буля. Алгебра  , побудована на базисі функцій кон’юнкції, додавання за модулем два та функції-константи одиниці, називається алгеброю Жегалкіна.
, побудована на базисі функцій кон’юнкції, додавання за модулем два та функції-константи одиниці, називається алгеброю Жегалкіна.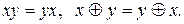






 .
.






 .
. , а також поглинання
, а також поглинання  . Отримаємо скорочену диз’юнктивну нормальну форму, яка визначає кожну формулу однозначно.
. Отримаємо скорочену диз’юнктивну нормальну форму, яка визначає кожну формулу однозначно. .
. , тобто це і є мінімальна ДНФ.
, тобто це і є мінімальна ДНФ. ;
;  ;
;  , отримаємо
, отримаємо

 , з’єднаних певними способами лініями. Кожна пара вершин
, з’єднаних певними способами лініями. Кожна пара вершин  , що з’єднана лінією, називається ребром графа і позначається
, що з’єднана лінією, називається ребром графа і позначається  . Якщо при розв’язанні задачі суттєвим є напрямок цієї лінії, тоді у графічному зображенні цей напрямок фіксується стрілкою, а ребро називають дугою. Вершини
. Якщо при розв’язанні задачі суттєвим є напрямок цієї лінії, тоді у графічному зображенні цей напрямок фіксується стрілкою, а ребро називають дугою. Вершини  називається початковою, а
називається початковою, а  – кінцевою вершинами дуги
– кінцевою вершинами дуги  . Таким чином, граф G являє собою пару
. Таким чином, граф G являє собою пару  , де
, де  – множина вершин, а
– множина вершин, а  – множина дуг графа.
– множина дуг графа. та
та  називаються суміжними, якщо існує спільна для них обох вершина.
називаються суміжними, якщо існує спільна для них обох вершина. 1. Найбільш наочним способом задання графа є малюнок, де вершини зображаються точками на площині, а дуги (ребра) лініями з (без) стрілок, що визначають напрямок зв’язку.
1. Найбільш наочним способом задання графа є малюнок, де вершини зображаються точками на площині, а дуги (ребра) лініями з (без) стрілок, що визначають напрямок зв’язку. ,
, 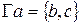 ,
,  ,
,  ,
,  .
. .
.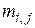 дорівнює 1 у випадку, коли у графі існує дуга
дорівнює 1 у випадку, коли у графі існує дуга  дорівнює -1 у випадку, коли дуга
дорівнює -1 у випадку, коли дуга  із вершиною
із вершиною  . Наведемо один із алгоритмів розв’язку цієї задачі (алгоритм послідовної індексації вершин).
. Наведемо один із алгоритмів розв’язку цієї задачі (алгоритм послідовної індексації вершин). . Тоді для вершин індексу
. Тоді для вершин індексу 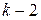 . Цей процес продовжуємо доти, поки не потрапимо у початкову вершину
. Цей процес продовжуємо доти, поки не потрапимо у початкову вершину  . Наведемо один із алгоритмів розв’язку цієї задачі (алгоритм Форда).
. Наведемо один із алгоритмів розв’язку цієї задачі (алгоритм Форда). . Отже, всі всі вершини графа є проіндексованими. Якщо вершини
. Отже, всі всі вершини графа є проіндексованими. Якщо вершини  та
та  є суміжними і проіндексовані відповідно
є суміжними і проіндексовані відповідно  та
та  , а для їх індексів виконується нерівність:
, а для їх індексів виконується нерівність:  , де
, де  – вага дуги
– вага дуги  , тоді вершині
, тоді вершині  . Таким чином, здійснюємо процес переіндексації вершин, тобто корекцію проводимо для всіх індексів, для яких це можливо, до тих пір, поки всі проставлені індекси не стануть мінімально можливими. Якщо вершина
. Таким чином, здійснюємо процес переіндексації вершин, тобто корекцію проводимо для всіх індексів, для яких це можливо, до тих пір, поки всі проставлені індекси не стануть мінімально можливими. Якщо вершина  становить довжину найкоротшого шляху в зваженому графі, а встановлення послідовності вершин цього мінімального шляху здійснюється аналогічно до вказаного у першому пункті способу.
становить довжину найкоротшого шляху в зваженому графі, а встановлення послідовності вершин цього мінімального шляху здійснюється аналогічно до вказаного у першому пункті способу. , то це означає, що шляху із вершини
, то це означає, що шляху із вершини  у вершину
у вершину  у заданому графі. Для розв’язання цієї задачі необхідно спершу побудувати відповідну матрицю суміжності для заданого графа. Далі піднести цю матрицю до степеня k. Значення елемента
у заданому графі. Для розв’язання цієї задачі необхідно спершу побудувати відповідну матрицю суміжності для заданого графа. Далі піднести цю матрицю до степеня k. Значення елемента  .
. .
. та g, оскільки у матриці суміжності цим вершинам відповідає нульовий рядок, а стовпець не нульовий. Вершина виходу – k, оскільки рядок, відповідний цій вершині, у матриці суміжності не нульовий, а стовпець – нульовий.
та g, оскільки у матриці суміжності цим вершинам відповідає нульовий рядок, а стовпець не нульовий. Вершина виходу – k, оскільки рядок, відповідний цій вершині, у матриці суміжності не нульовий, а стовпець – нульовий. , а також існують двонаправлені дуги, такі як
, а також існують двонаправлені дуги, такі як  і
і  .
. ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  ;
;  .
. .
. ,
,
 .
. матриці
матриці  . Отже, кількість шляхів дорівнює 2.
. Отже, кількість шляхів дорівнює 2. матриці
матриці  . Отже, кількість контурів дорівнює 4.
. Отже, кількість контурів дорівнює 4. — множини. Довести тотожність:
— множини. Довести тотожність:












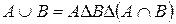
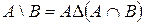















 ,
,  ,
, ,
,  ,
, 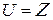 .
.










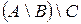




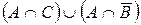











 ;
;  ;
;  R–множина дійсних чисел. Перевірити, чи будуть рівнопотужними множини
R–множина дійсних чисел. Перевірити, чи будуть рівнопотужними множини 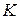 і
і 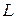 .
.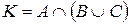 ;
; 
 ;
; 
 ;
; 
 ;
; 
 ;
; 
 ;
; 
 ;
; 
 ;
; 
 ;
;  ;
; 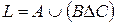
 ;
; 
 ;
; 
 ;
; 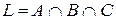
 ;
; 
 . У завданнях 1–10 встановити:
. У завданнях 1–10 встановити: карт.
карт. ) так, щоб було чотири карти однакового номеру.
) так, щоб було чотири карти однакового номеру. . У завданнях 21–30 встановити:
. У завданнях 21–30 встановити: ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; .
. ,
,  ;
; ,
,  ;
; ,
, 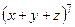 ;
; ;
;