 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Телеграфные сообщения и их характеристики 12
В предыдущей лекции упоминалось, что информация для передачи по сети электросвязи должна быть представлена в виде сообщения. Сообщения обычно делятся на два основных класса: аналоговые (непрерывные) и дискретные. Аналоговые сообщения представимы функциями Количество информации, которое содержится в сообщении
Величина
Двоичная единица информации, которая может принимать только два значения (например, ноль или единица), называется битом. Если вероятности появления этих значения равны – 0,5 и 0,5 – то Количество информации, содержащейся в нескольких независимых друг от друга сообщениях, равно сумме количества информации в каждом их них. Это правило основано на интуитивных представлениях об увеличении количества информации при получении нескольких сообщений. В качестве примера оценим количество информации в слове из семи букв при условии, что алфавит содержит 32 буквы. Будем считать, что все вероятности появления каждой буквы одинаковы. Тогда:
Для решения ряда задач необходимо оценивать информационные свойства источника сообщений в целом. В качестве такой оценки используется среднее значение количества информации, связанное с одним сообщением. Оно называется энтропией источника сообщений. В тексте частота появления разных букв отличается весьма существенно. Поэтому для всех значений
Соотношение (2.4) основано на предположении, что все сообщения источника информации независимы. Источнику зависимых сообщений свойственна избыточность. Если в последовательности сообщений существует статистическая связь, то некоторую часть информации можно не передавать. Она восстанавливается на приеме благодаря известной статистической связи. Характерный пример – исключение из телеграмм союзов, предлогов и знаков препинания. Они восстанавливаются за счет известных правил построения слов и фраз, которые – в данном случае – служат примером статистической связи. Одно из важных направлений в развитии теории и практики электросвязи – сокращение избыточности сообщений. Важной характеристикой источника сообщений считается его производительность. Она выражается средним значением количества информации, создаваемым источником в единицу времени. Самая большая производительность свойственна источнику сообщений с максимальной энтропией.
12 |



 , которые непрерывны. Характерный пример – передача речи в тот период, когда абонент говорит. Дискретные сообщения представляют собой набор элементов, образующих конечное множество. Типичным примером дискретных сообщений может служить телеграмма, состоящая из набора букв, цифр и служебных символов.
, которые непрерывны. Характерный пример – передача речи в тот период, когда абонент говорит. Дискретные сообщения представляют собой набор элементов, образующих конечное множество. Типичным примером дискретных сообщений может служить телеграмма, состоящая из набора букв, цифр и служебных символов. , принято оценивать по вероятности его появления –
, принято оценивать по вероятности его появления –  . Тогда весьма вероятное сообщение содержит незначительный объем новых сведений. Существенный объем новых данных присущ маловероятным сообщениям. Принято оценивать количество информации –
. Тогда весьма вероятное сообщение содержит незначительный объем новых сведений. Существенный объем новых данных присущ маловероятным сообщениям. Принято оценивать количество информации –  логарифмом величины, обратной вероятности
логарифмом величины, обратной вероятности  . (2.1)
. (2.1)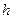 , основание логарифма, служит мерой того способа представления информации, который используется для обмена сообщениями. Чаще всего предполагается, что
, основание логарифма, служит мерой того способа представления информации, который используется для обмена сообщениями. Чаще всего предполагается, что  :
: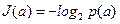 . (2.2)
. (2.2) . Это означает, что количество информации равно одному биту. Если
. Это означает, что количество информации равно одному биту. Если  , то количество информации всегда равно нулю –
, то количество информации всегда равно нулю –  .
. . (2.3)
. (2.3) определяются вероятности
определяются вероятности  и соответствующие оценки
и соответствующие оценки  . Энтропия источника
. Энтропия источника  сообщений определяется как математическое ожидание количества информации:
сообщений определяется как математическое ожидание количества информации: . (2.4)
. (2.4)