 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Свертка функций. Отыскание оригинала по изображению. 12
Таблица изображений некоторых элементарных оригиналов.
Приведем примеры использования определения и результатов утверждений для нахождения изображений.
Тогда по теореме о дифференцировании получим:
Последовательно вычисляя производные, находим:
Окончательно запишем:
Свертка функций. Отыскание оригинала по изображению.
Сверткой функций Отметим, что операция свертывания обладает свойством коммутативности: Утверждение 10 (об умножении изображений, или теорема о свертке). Пусть Таким образом, изображением свертки двух оригиналов является произведение их изображений.
Первый способ. Воспользуемся таблицей изображений: Воспользовавшись теоремой о свертке, запишем: Итак, изображение свертки найдено. Найдем саму свертку. Для этого, как и в предыдущей задаче, с помощью метода неопределенных коэффициентов представим дробь в виде суммы простейших дробей: Второй способ. Вычислим свертку функций, воспользовавшись определением: Интегрируем по частям: Теперь по таблице изображений находим изображение свертки: Итак, нами получен тот же результат.
Таким образом, Заметим, что в данном случае оригинал можно было найти и по таблице изображений. При нахождении оригиналов по заданным изображениям можно использовать несколько приемов. Первый состоит в том, что изображение Второй способ состоит в том, чтобы представить дробь в виде произведения дробей, каждая из которых является изображением некоторой функции, и применить теорему о свертке. Третий способ основан на следующем утверждении: Утверждение 11 (о разложении). Пусть функция Отметим, что данное утверждение допускает некоторое упрощение в случае, когда а) все корни многочлена, стоящего в знаменателе изображения имеют кратность единица: б) корни многочлена, стоящего в знаменателе изображения кратные:
Приведем примеры использования вышеперечисленных идей при решении задач.
Аналогично преобразуем второе слагаемое в выражении: Для нахождения оригинала, соответствующего третьему слагаемому Для нахождения оригинала, соответствующего последнему слагаемому Итак, оригинал, соответствующий нашему изображению имеет вид:
Воспользуемся стандартной техникой нахождения неопределенных коэффициентов Слева и справа у нас многочлены. По теореме о равенстве двух многочленов два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях неизвестного. Тогда запишем соответствующую систему и вычислим коэффициенты разложения:
Таким образом, исходную дробь представим в виде Следовательно, Проиллюстрируем теперь использование теоремы о разложении для нахождения оригиналов, соответствующих изображениям.
Следовательно, имеем право, записать
При этом Итак, корни многочлена знаменателя: Найдем соответствующие коэффициенты: Следовательно, Приведем также пример ситуации с кратными корнями.
Найдем коэффициенты этого разложения
?????????? Методы операционного исчисления удобно использовать при решении некоторых дифференциальных и интегро-дифференциальных уравнений, а также систем таких уравнений. При этом предполагают, что в правой части такого уравнения стоит оригинал некоторой функции. Приведем примеры использования утверждений, касающихся свойств оригиналов и изображений.
Правая часть уравнения преобразуется следующим образом:
Приходим к операторному уравнению: Выразим из полученного уравнения изображение
Найдем разложение получившейся дроби на сумму дробей, представляющих собой оригиналы элементарных функций.
Следовательно,
Выразим отсюда
И значит решением исходного уравнения будет функция
Выразим из получившейся операторной системы
Отметим, что для нахождения соответствующих оригиналов удобно воспользоваться теоремой разложения, учтя при этом, что корни знаменателя имеют первую кратность. Таким образом
Поэтому ее изображение можно найти, используя формулу преобразования Лапласа, учитывая области определения кусочно-заданного оригинала:
12 |



















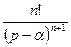










 Найти изображение функции
Найти изображение функции  , используя преобразование Лапласа.
, используя преобразование Лапласа. является оригиналом. Так как
является оригиналом. Так как  для всех
для всех  , то изображение
, то изображение  этой функции будет определено и аналитично в полуплоскости
этой функции будет определено и аналитично в полуплоскости  . Далее находим:
. Далее находим: .
.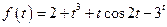
 .
. .
. , воспользовавшись свойством дифференцирования изображений.
, воспользовавшись свойством дифференцирования изображений. .
. .
. и далее
и далее  .
. .
. .
. . Тогда по теореме об интегрировании оригинала имеем право, записать:
. Тогда по теореме об интегрировании оригинала имеем право, записать: .
. будем называть функцию
будем называть функцию  .
. , то есть
, то есть  .
. ;
;  . Тогда
. Тогда  .
. и
и  :
: и
и  .
. .
. . Тогда по таблице изображений запишем:
. Тогда по таблице изображений запишем:  .
. .
.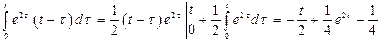 . Следовательно,
. Следовательно,  .
.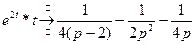 .
. .
. . По теореме о свертке имеем:
. По теореме о свертке имеем:  . Найдем теперь свертку функций
. Найдем теперь свертку функций  и
и  :
:
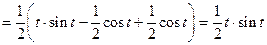 .
. .
. представляется в виде суммы элементарных дробей, каждая из которых является изображением простых оригиналов. Далее, используя таблицу оригиналов и свойство линейности преобразования Лапласа, находят оригинал, соответствующий исходной дроби.
представляется в виде суммы элементарных дробей, каждая из которых является изображением простых оригиналов. Далее, используя таблицу оригиналов и свойство линейности преобразования Лапласа, находят оригинал, соответствующий исходной дроби. представляет собой правильную рациональную дробь, имеющую полюсы в точках
представляет собой правильную рациональную дробь, имеющую полюсы в точках  , где
, где  . Тогда оригиналом для неё служит функция
. Тогда оригиналом для неё служит функция  , где сумма берется по всем полюсам.
, где сумма берется по всем полюсам.

 ,
,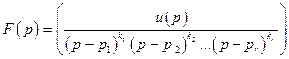
 ,
,  .
. .
. . Поэтому, по свойству линейности преобразования Лапласа, находим соответствующий оригинал:
. Поэтому, по свойству линейности преобразования Лапласа, находим соответствующий оригинал:  .
.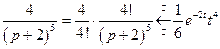 .
. выделим полный квадрат в знаменателе:
выделим полный квадрат в знаменателе:  . С учетом этого запишем:
. С учетом этого запишем:  . Окончательно для этого слагаемого получим:
. Окончательно для этого слагаемого получим:  .
. , воспользуемся утверждением запаздывания оригинала. Так как оригинал
, воспользуемся утверждением запаздывания оригинала. Так как оригинал 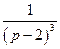 :
:  , то, применив теперь теорему запаздывания оригинала, имеем
, то, применив теперь теорему запаздывания оригинала, имеем 
 .
. .
.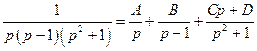 .
. . Приведем правую часть равенства к общему знаменателю. Тогда дроби равны, знаменатели равны, а значит, и числители равны:
. Приведем правую часть равенства к общему знаменателю. Тогда дроби равны, знаменатели равны, а значит, и числители равны:  .
. .
. .
. .
. .
. ,
,  и полюс первого порядка
и полюс первого порядка  . Тогда по тереме о разложении оригиналом для
. Тогда по тереме о разложении оригиналом для  . Вычислим соответствующие вычеты
. Вычислим соответствующие вычеты  .
. ,
, ,
,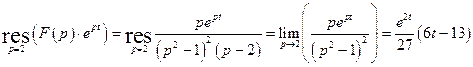 .
. .
. .
. , а
, а  и
и  .
. .
. ,
,  ,
,  ,
,  .
. .
.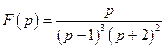 .
. .
. ;
; ;
;
 ;
; ;
;
 Найти частное решение дифференциального уравнения
Найти частное решение дифференциального уравнения .
. , удовлетворяющая данному уравнению имеет изображение:
, удовлетворяющая данному уравнению имеет изображение: 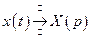 . Тогда воспользовавшись утверждением о дифференцируемости оригинала запишем:
. Тогда воспользовавшись утверждением о дифференцируемости оригинала запишем: , а
, а  .
. .
. .
. частного решения дифференциального уравнения:
частного решения дифференциального уравнения: .
. .
.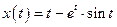 решение исходной задачи Коши.
решение исходной задачи Коши. .
. . И пусть
. И пусть  и
и  , кроме того
, кроме того  . И соответствующее операторное уравнение имеет вид:
. И соответствующее операторное уравнение имеет вид:  .
. .
.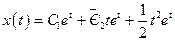 . (здесь
. (здесь  ).
). .
. ).
). . Выразим функцию изображения
. Выразим функцию изображения  . Найдем оригинал, соответствующий данному изображению
. Найдем оригинал, соответствующий данному изображению  .
.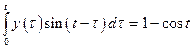 .
. и
и  . Выражая из последнего уравнения
. Выражая из последнего уравнения 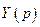 убедимся
убедимся  . И, значит, этому изображению соответствует оригинал
. И, значит, этому изображению соответствует оригинал  .
.
 .
. ,
,  .
. , и
, и  .
. (см. рис.)
(см. рис.)

 .
.


 .
.
 . Это легко проверяется графическим сложением функций
. Это легко проверяется графическим сложением функций  ,
,  и т.д., изображенных на одном и том же чертеже. По теореме запаздывания получаем:
и т.д., изображенных на одном и том же чертеже. По теореме запаздывания получаем: 
 . Второй сомножитель из правой части равенства представляет собой геометрическую прогрессию, со знаменателем
. Второй сомножитель из правой части равенства представляет собой геометрическую прогрессию, со знаменателем  . Так как,
. Так как,  , то геометрическая прогрессия сходится, и получаем:
, то геометрическая прогрессия сходится, и получаем:  .
.