 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Закон Дальтона— основной закон газовой смеси.
Лекция 5. Смеси идеальных газов. Смеси газов и их параметры. На практике зачастую необходимо исследование тепловых процессов, в которых участвуют смеси газов: поведение воздуха и испарившегося топлива в камерах сгорания различных двигателей, явления движения продуктов сгорания и взрыва, испарения и конденсации паров воды в воздухе и т. д. Для этой цели необходимо иметь модели смеси реальных газов. Следует отметить, что смеси реальных газов при малых давлениях и больших температурах, в том числе и воздух в обычных условиях, хорошо описываются модель идеального газа. Поэтому в дальнейшем все смеси реальных газов будем считать идеальным газом. Как известно, модель идеального газа основана на уравнении состояния вида Здесь все параметры, кроме газовой постоянной R, могут быть определены опытным путем, поэтому задача построения модели смеси газов основана на определении газовой постоянной R для смеси. Однако проще сначала определить не R, а киломольную массу смеси
Здесь Rm — универсальная газовая поставная, Rm=8314 Дж/(кмоль×К). Рассмотрим основные свойства смеси идеальных газов, необходимые для определения Закон Дальтона— основной закон газовой смеси. Основной закон газовой смеси — закон Дальтона (1801 г.): каждый отдельный газ ведет себя в газовой смеси так, как если бы он один при температуре смеси занимал весь объем смеси. Следствие из закона Дальтона: каждый отдельный газ в смеси оказывает на стенки сосуда такое давление, как если бы он один занимал объем смеси. Давление каждого компонента смеси называется парциальным давлением и обозначается для i- го компонента смеси как pi. Это следствие из закона Дальтона можно записать так: давление газовой смеси p равно сумме парциальных давления pi ее компонентов:
Здесь k — число компонентов смеси; Приведем очевидные равенства, необходимые в дальнейшем. Масса всей смеси равна сумме масс ее компонентов:
Здесь Количество вещества смеси равно сумме количества вещества ее компонентов
Здесь Очевидно, что каждый газ из состава смеси имеет температуру T смеси и объем V смеси. Если молекулы смеси разделить так, чтобы каждый компонент смеси занял свою часть объем Vi объема смеси V, то давление всех газов смеси будет одинаковым и равным давлением p газовой смеси. Такие объемы Vi называют парциальными объемами, приведенными к давлению смеси, или приведенным объемами. Для них справедлив закон Амага: сумма парциальных объемов смеси равна объему смеси
Здесь Как уже было отмечено, температура компонентов Ti равна температуре смеси T
Одним из важных свойств газовой смесей является равенство относительных парциальных давлений
Чтобы показать справедливость этих равенств, рассмотрим два уравнения состояния: первое — для i-го компонента смеси с массой
Здесь
Так как правые части этих равенств равны, то равны и левые: отсюда
Осюда
Чтобы завершить доказательства справедливости равенств (3.7), опять рассмотрим два уравнения состояния: первое — для n киломолей смеси
второе — для ni киломолей i-го компонента смеси в парциальном объеме
Разделив последнее из этих равенств на первое, получим
Учитывая равенство (3.8) и последнее соотношение, получим равенства (3.7). Заметим, что в эти равенства не входят относительные массовые концентрации Заметим, что массовые доли
|



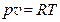
 , а затем найти R из равенства
, а затем найти R из равенства

 — относительное парциальная давление i-го компонента смеси.
— относительное парциальная давление i-го компонента смеси.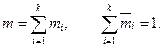
 — массовая концентрация в смеси i-го компонента.
— массовая концентрация в смеси i-го компонента.
 — киломольная (мольная) концентрация в смеси i- го компонента.
— киломольная (мольная) концентрация в смеси i- го компонента.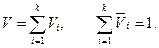
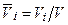 — относительная объемная концентрация i- го компонента смеси.
— относительная объемная концентрация i- го компонента смеси.
 , объемов
, объемов  и киломольных концентраций
и киломольных концентраций 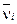
 (3.7)
(3.7) и давлением
и давлением 
 — газовая постоянная i-го компонента; второе — для этого же компонента, но только в парциальном (приведенном) объеме
— газовая постоянная i-го компонента; второе — для этого же компонента, но только в парциальном (приведенном) объеме 

 (3.8)
(3.8)
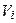

 или
или 
 компонент смеси, следовательно, все способы задание смеси, кроме массовых, равнозначны.
компонент смеси, следовательно, все способы задание смеси, кроме массовых, равнозначны. и другие (
и другие (  ) по формуле
) по формуле (3.9)
(3.9)