 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Сравнение двух выборочных средних. t-критерий Стьюдента.
При сравнении данных двух выборок на основании расчета t-критерия Стьюдента группы могут различаться: 1.по объему входящих в них данных: а) обе группы большие (n>30); б) обе группы малые (n<30); в) одна- большая (n>30), другая малая (n<30). 2.по своему составу: а) группы с зависимыми вариантами, когда i-тая варианта первой группы сравнивается с i-той вариантой второй группы (сравнение результатов повторных тестирований одной и той же выборки, nx=ny ); б) группы с независимыми вариантами (можно менять варианты местами внутри выборки, т. е. данные тестирования по одному и тому же показателю у разных групп). При применении методов сравнения, основанных на расчете t-критерия, необходимо производить расчет числа степеней свободы. Под числом степеней свободы понимают разность между числом измеряемых (наблюдаемых) значений и числом линейных отношений (связей ), возникающих между ними. Для критерия Стьюдента расчет степеней свободы производится по формуле: К=nx+ny-2, где nx-объем выборки X, где ny- объем выборки Y. При сравнение двух больших или одной большой и одной малой групп с независимыми вариантами применяют формулу:
где
Сравнение двух малых групп с независимыми вариантами проводится по формуле:
Сравнение двух малых групп с зависимыми вариантами проводится по формуле: где Расчет степеней свободы в данном случае, т. к. nx=ny, проводиться по формуле: К=2·(n-1). После того как произведен расчет t- критерия Стьюдента и числа степеней свободы, из таблицы t- критерия Стьюдента находится критическое значение t- критерия для трех порогов доверительной вероятности β и уровней значимости α. Если tф<tst (минимального значения из таблицы), то между данными двух выборок не наблюдается достоверности различий, то есть они примерно равные по данному показателю, и, следовательно, предположение о различиях в показателях выборок оказывается ошибочным. Если же tф> tst, то говорят о достоверности различий при определенной доверительной степени доверительной вероятности. Корреляционный анализ и регрессионный анализ. Общие сведения Статистической называется зависимость между случайными величинами, при которой изменение одной из величин влечет за собой изменение закона распределения другой величины. Односторонняя вероятностная зависимость между случайными есть регрессия. Она устанавливает соответствие между этими величинами. Виды регрессии: 1.Регрессия относительно числа переменных: - Простая регрессия – регрессия между двумя Множественная регрессия – это регрессия между зависимой переменной переменой у и несколькими объясняющими переменными х1, х2, …, хn. Множественная линейная регрессия имеет следующий вид: У= а0 + а1х1 + а2х2 + …+ аnxn, Где: у – функция регрессии; х1,х2, …, хn - независимые переменные; а1, а2, …, аn – коэффициенты регрессии; а0 - свободный член уравнения; n – число факторов, включаемых в модель.
1. Регрессия относительно формы зависимости: - линейная регрессия, выражаемая линейной функцией; - нелинейная регрессия, выражаемая нелинейной функцией. 2. В зависимости от характера регрессии различают следующие ее виды: - положительную регрессию. Она имеет место, если с увеличением (уменьшением) объясняющей переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются); - отрицательную регрессию. В этом случае с увеличением или уменьшением объясняющей переменной зависимая переменная уменьшается или увеличивается. 3. Относительно типа соединения явлений различают: - непосредственную регрессию. В этом случае зависимая и объясняющая переменные связаны непосредственно друг с другом; - косвенную регрессию. В этом случае объясняющая переменная действует на зависимую через ряд других переменных; - ложную регрессию. Она возникает при формальном подходе к исследуемым явлениям без уяснения того, какие причины обуславливают данную связь. Регрессия тесно связана с корреляцией. Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. Понятия «корреляция» и «регрессия» тесно связаны между собой. В корреляционном анализе оценивается сила связи, а регрессионном анализе исследуется ее форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию. Корреляция, как и регрессия, имеет различные виды: 1. Относительно характера корреляции различают: · положительную; · отрицательную. 2. Относительно числа переменных – · простую; · множественную; · частную. 3. Относительно формы связи – · линейную; · нелинейную. 4. Относительно типа соединения – · непосредственную; · косвенную; · ложную.
Исследование корреляционных связей называется корреляционным анализом, а исследование односторонних стохастических зависимостей – регрессионным анализом.
Линейная регрессия Пусть задана система случайных величин Х и Y и случайные величины Х и Y зависимы. Представим одну из случайных величин как линейную функцию другой случайной величины Х: Y= g(x) = a + bx, где a, b - параметры, которые подлежат определению. Эти параметры могут быть определены различными способами, наиболее часто используется метод наименьших квадратов (МНК). Функцию g(x) называют наилучшим приближением в смысле МНК, если математическое ожидание М[Y-g(x)]2 принимает возможное наименьшее значение. В этом случае функцию g(x) называют средней квадратической регрессией Y на X. Рассмотрим определение параметров выбранного уравнения прямой линии средней квадратической регрессии по не сгруппированным данным. Пусть изучается система количественных признаков (Х ,Y), т.е. ведутся наблюдения за случайной двухмерной величиной (Х , Y). Пусть в результате n наблюдений получено n пар чисел (х1,у1), (х2, у2), …, (хn, yn). Требуется по полученным данным найти выборочное уравнение прямой линии средней квадратической регрессии:
Поскольку данные несгруппированные, т.е. каждая пара чисел встречается один раз, то можно перейти от условной средней к переменной у. Угловой коэффициент k обозначим через k = p и назовем ее выборочной оценкой коэффициента регрессии Итак, требуется найти: Метод наименьших квадратов (МНК) получили систему двух линейных уравнений относительно p и b. Решая эту систему, получим:
Основные понятия корреляционно-регрессионного анализа 1. Среднее значение переменной определяется по следующей формуле:
где х1 – эмпирическое значение переменной х; n – число наблюдений. Дисперсия
2. Коэффициент корреляции
Коэффициент корреляции характеризует тесноту или силу связи между переменными у и х. Значения, переменные rху, заключены в пределах от –1 до +1. При положительном значении rху имеет место положительная корреляция, т.е. с увеличением (уменьшением) значений одной переменной (х) значение другой (у) соответственно увеличивается (уменьшается). При отрицательном значении rху имеет место отрицательная корреляция, т.е. с увеличением (уменьшением) значений х значения у соответственно уменьшаются (увеличиваются). При изучении экономического явления, зависящего от многих факторов, строится множественная регрессионная зависимость. В этом случае для характеристики тесноты связи используются коэффициент множественной корреляции:
где s2ост – остаточная дисперсия зависимой переменной; s2общ – общая дисперсия зависимой переменной.
3. Общая дисперсия определяется по формуле:
Величина s2общ характеризует разброс наблюдений фактических значений от среднего значения Остаточная дисперсия определяется по следующей формуле:
где уiт – теоретические значения переменной у, полученные по уравнению регрессии при подстановке в него наблюдаемых фактических значений хi. Остаточная дисперсия характеризует ту часть рассеяния переменной у, которая возникает из-за всякого рода случайностей и влияния неучтенных факторов. 4. Коэффициент детерминации служит для оценки точности регрессии, т.е. соответствие полученного уравнения регрессии имеющимся эмпирическим данным, и вычисляется по формуле
Изменяется Д в пределах от 0 до 1, т.е. 0 £ Д £ 1 Модель считается тем точнее, чем ближе Д к 1, т.е. чем меньше s2ост. Стандартная ошибка оценки равна Если Д=0, это значит отношение Д = 1 , значит, 8. Корреляционное отношение используется для оценки тесноты связи между двумя явлениями, в частности для определения тесноты связи
|



 ,
, ,
,  - величины средних выборок Х и Y;
- величины средних выборок Х и Y; ,
,  - стандартные ошибки средних выборок Х и Y.
- стандартные ошибки средних выборок Х и Y. .
. ,
, ;
; 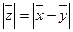 ; n - число испытуемых
; n - число испытуемых
 .
.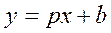
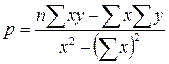 ;
; .
.




 .
.

 .
. , т.е. s2ост = s2общ, и, следовательно,
, т.е. s2ост = s2общ, и, следовательно, 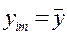 . В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если
. В этом случае прямая регрессии будет параллельна оси X, корреляционно-регрессионная связь между X и Y отсутствует. Если , т.е. s2ост = 0. Отсюда уi = yiT т. е наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная.
, т.е. s2ост = 0. Отсюда уi = yiT т. е наблюдаемые точки лежат на построенной прямой, следовательно, зависимость функциональная. исходного ряда уi, с теоретическим рядом yiT . Корреляционное отношение определяют по данным, сгруппированным по объясняющей переменной по следующей формуле:
исходного ряда уi, с теоретическим рядом yiT . Корреляционное отношение определяют по данным, сгруппированным по объясняющей переменной по следующей формуле: