 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Функція розподілу випадкової величини.
ТЕОРІЯ ЙМОВІРНОСТЕЙ
Подія - одне з основних понять теорії ймовірностей. Воно є первісним і немає означення. Події настають (відбуваються, з'являються) при виконанні певної сукупності умов S. Кожна реалізація цих умов називається експериментом (випробовуванням, іспитом). Приклад 1. Стрілець стріляє по мішені, яку поділено на 4 області. Постріл - це експеримент, а попадання в певну область - подія. Випадковою подією (можливою подією чи просто подією)називається будь-який факт, що у результаті випробування може відбутися чи не відбутися. Нехай простір елементарних подій є скінченною множиною
тобто є лише N можливих результатів випробування, отже, множина Ω є повною групою всіх попарно несумісних результатів випробування. Класичне означення ймовірності формулюють для подій, які є підмножинами множини Ω. Якщо
то ймовірність події А визначають за формулою:
де N(A) – кількість елементів множини А. Отже, ймовірністю події А називається відношення кількості сприятливих для події А елементарних подій до кількості всіх рівноможливих і попарно несумісних результатів випробування. Геометричні ймовірності Класичне означення ймовірності не можна застосувати до випробування, для якого множина Ω є незліченною множиною елементарних подій. Нехай простір елементарних подій Ω – це відрізок числової прямої або область на площині, або в просторі, а елементарні події ω – окремі точки в межах цієї області. Припустимо, що область Ω має скінченну міру Означення. Геометричною ймовірністю події А називається відношення міри Можна показати, що геометрична ймовірність задовольняє всі аксіоми теорії ймовірностей.
2. Властивості ймовірності. Класичне означення ймовірності. Властивості ймовірності Розглянемо частковий випадок уведеного означення. Будемо вважати, що всі n елементарних подій мають одну і ту ж ймовірність, тобто ймовірність, що дорівнює числу
Якщо ймовірність події визначається за допомогою цього відношення, то таке означення ймовірності називається класичним. Ті елементарні події, з яких складається подія А, називають подіями (випадковими), що сприяють появі події А. Означення. Ймовірністю події А називається таке відношення кількості випадків, що сприяють появі події А, до кількості всіх випадків. Властивості ймовірності. 1. 2.
Нехай:
3.
4.
Подія А спричиняє подію В і позначається АÌВ, якщо множина А є підмножиною множини В.
попадаємо в В. 5.
6. Нехай А та В –g події
3. Умовна ймовірність. Формула повної ймовірності. Формули Бейєса. Умо́вна ймові́рність — ймовірність однієї події за умови, що інша подія вже відбулася. Нехай
Властивості Прямо з визначення очевидно випливає, що
Якщо Умовна ймовірність є ймовірністю, тобто функція
задовольняє всім аксіомам імовірнісної міри. Формула повної ймовірності дозволяє обчислити ймовірність деякої події через умовні ймовірності цієї події в припущенні якихось гіпотез, а також ймовірностей цих гіпотез. Визначення Нехай дано імовірнісний простір
Зауваження Формула повної ймовірності також має наступну інтерпретацію. Нехай N - випадкова величина, що має розподіл
Тоді
тобто апріорна ймовірність події рівна середньому його апостеріорній ймовірності. Теоре́ма Ба́єса — одна з основних теорем теорії ймовірностей, яка визначає ймовірність настання події, коли відома тільки часткова інформація про подію. Названа на честьТомаса Баєса. Формула Баєса:
де P(A) — апріорна ймовірність гіпотези A; P(A | B) — ймовірність гіпотези A при настанні події B (апостеріорна ймовірність); P(B | A) — ймовірність настання події B при істинності гіпотези A; P(B) — ймовірність настання події B. Формула виводиться із визначення умовної ймовірності:
Наслідок Важливим наслідком формули Баєса є формула повної ймовірності події, що залежить від декількох несуміснних гіпотез (і тільки від них).
4. Схема незалежних випробувань. Граничні теореми. Схема незалежних випробувань Бернуллі Проводяться n дослідів, у кожному з яких може настати певна подія ("успіх") з ймовірністю p (або не настати - "неуспіх" - q = 1 - p). Знайти ймовірність отримати k успіхів у досліді. Нехай при незмінних умовах проводяться послідовні пов-торні випробування, в результаті яких можуть бути два мож- ливі наслідки (дві елементарні події А і A ): певна подія А відбувається і не відбувається A . Оскільки імовірність події А в кожному випробуванні не залежить від наслідку (ре-зультату) інших випробувань, то такі випробування нази-вають незалежними. Якщо в кожному незалежному випро-буванні імовірність настання події А одна й та сама і дорівнює р (0 < р < 1) і не залежить від номера випробування, то такі випробування називаються схемою Бернуллі. Рассмотрим випадок багаторазового повторення однієї й тієї ж випробування чи випадкового експерименту. Результат кожного випробування вважатимемо які залежать від цього, який результат припало на попередніх випробуваннях. Як результатів чи елементарних фіналів кожного окремого випробування будемо розрізняти лише дві возможности: 1) поява деякого події А; 2) поява події Пусть ймовірність P(A) появи події А постійна і дорівнює p (0.p1). Можливість P( Примерами таких випробувань можуть быть: 1) підкидання монети: А – випадання герба; P(A) = P( 2) кидання гральною кістки: А – випадання кількості очок, рівного п'яти, P(A) =1/6, P( 3) вилучення наудачу з урни, що містить 7 білих хусток і 3 чорних кулі, одного кулі (з поверненням): А – вилучення білого кулі, P(A) = 0,7; P( Пусть вироблено n випробувань, які ми розглядати, як одне складне випадковий експеримент. Складемо таблицю з n клітин, розміщених у ряд, пронумеруємо клітини, і результати кожного випробування відзначатимемо так: тоді як 1-му випробуванні подія А сталося, то i-ю клітину ставимо цифру 1, якщо подія А сталося (відбулася подія Если, наприклад, проведено 5 випробувань, й цю подію А відбулося лише у 2-му і 5-му випробуваннях, то результат можна записати такий послідовністю нулів і одиниць: 0; 1; 0; 0; 1. Каждому можливого результату n випробувань відповідатиме послідовність n цифр 1 чи 0, які чергуються у порядку, у якому з'являються події A і 1; 1; 0; 1; 0; 1; 0; 0; ... 0; 1; 1; 0 n цифр Всего таких послідовностей можна скласти Так як випробування незалежні, то ймовірність P кожної такої результату визначається шляхом перемножения ймовірностей подій A і P = p×p×q×p×q×p×q×q×...×q×p×p×q Если в написаної нами послідовності одиниця зустрічається x раз (це що означає, що нуль зустрічається n–x раз), то ймовірність відповідного результату буде pnqn-x незалежно від цього, у порядку чергуються ці x одиниць і n–x нулей. Все події, які у тому, що у n випробуваннях подія A сталося x раз, а подія Отсюда виходить формула Бернулли: Pn(x) = По формулі Бернуллі розраховується можливість появи події A " x " разів у n повторних незалежнихвипробуваннях, де p – можливість появи події A щодо одного випробуванні, q - можливість появи події Сформулированные умови проведення випробувань іноді називаються " схемою повторних незалежнихвипробувань " чи " схемою Бернуллі " Число x появи події A в n повторних незалежних випробуваннях називається частотой. Пример. З урни, що містить 2 білих хусток і 6 чорних куль, наудачу вибирається з поверненням 5 разів підряд один кулю. Підрахувати можливість, що 4 разу з'явиться білий шар. В наведених вище позначеннях n=8; p=1/4; q=3/4; x=5. Потрібну ймовірність обчислюємо по формулі Бернулли:
По формулі Бернуллі можна визначити ймовірності всіх можливих частот: x=0,1,2,3,4,5. Заметим, що тоді як цьому завданні вважати, що білих куль було 20000, а чорних 60000, то очевидно p і q залишаться незмінними. Однак у ситуації можна знехтувати поверненням витягнутого кулі після кожної вибірки (при дуже великих значеннях x) і слід вважати ймовірності всіх частот: x=0,1,2,... за такою формулою Бернулли. Формула Бернуллі при заданих числах p і n дає змоги розраховувати ймовірність будь-який частоти x (0 £ x £ n).
5. Випадкова величина. Функція розподілу випадкової величини. Щільність розподілу. Приклади. Випадковою величиною є будь-яка (не обов'язково числова) змінна Множина Властивості Випадкова величина X — це вимірна функція, визначена на даному вимірному просторі
Нехай x1, x2, … — значення випадкової величини X. Одне і те саме значення xj може відповідати, взагалі кажучи, різним елементарним подіям. Множина усіх цих елементарних подій утворює складену випадкову подію, що полягає в тому, що X = xj. Ймовірність цієї події позначається
визначає розподіл ймовірностей (слід відрізняти від функції розподілу ймовірностей) випадкової величини X. Очевидно, що:
Якщо дві або більше випадкових величини X1, X2, …, Xn визначено на одному просторі елементарних подій, то їх спільний розподіл задається системою рівнянь, в яких всім комбінаціям Випадкові величини називаються незалежними, якщо для довільної комбінації значень
Тобто, якщо Xk залежить лише від k-го випробування, то випадкові величини X1, X2, …, Xn взаємно незалежні. Ймовірність випадкової величини Ймовірність випадкової величини
де
Функція розподілу випадкової величини. Нехай дискретна випадкова величина задана законом розподілу. Розглянемо подію, яка полягає в тому, що випадкова величина Y прийме яке–небудь значення менше будь–якого числа X. Ця подія має певну ймовірність.
Позначимо При зміні X будуть змінюватися і ймовірності. Отже F(x) можна розглядати як функцію змінної величини X. Функцією розподілу випадкової величини Y називається функція F(x), яка виражає для кожного X ймовірність того, що Y прийме яке-небудь значення менше заданого. F(x) – постійна на інтервалах та має скачки в точках, що відповідають її значенням. Означення Нехай випадкова величина ξ є абсолютно неперервною, тоді її функція розподілу допускає представлення
де
Зауваження Функція густини імовірності існує лише для абсолютно неперервних випадкових величин. Властивості
6. Числові характеристики випадкової величини (математичне сподівання, дисперсія) та їх властивості. Функції розподілу ймовірностей як для дискретних, так і для неперервних випадкових величин дає повну інформацію про них. Проте на практиці немає потреби так докладно описувати ці величини, а достатньо знати лише певні параметри, що характеризують їх істотні ознаки. Так, наприклад, при вивченні розподілу заробітної платні цікавляться, по-перше, середньою платною та характеристикою розсіювання. Ці параметри й називають числовими характеристиками випадкових величин.
5.1.1 МАТЕМАТИЧНЕ СПОДІВАННЯ Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання (позначається ). Термін «математичне сподівання» випадкової величини є синонімом терміна «середнє значення» випадкової величини .
ОЗНАЧЕННЯ 5.1. Математичним сподіванням випадкової величини , визначеною на дискретному просторі , називається величина (сума ряду):
в тому випадку, коли цей ряд збігається абсолютно. Якщо - обмежена множина, то
ОЗНАЧЕННЯ 5.2. Математичним сподіванням випадкової величини , визначеною на неперервному просторі , називається величина
якщо цей інтеграл збігається абсолютно. Якщо = (- , то
Якщо = , то
5.1.2 ВЛАСТИВОСТІ МАТЕМАТИЧНОГО СПОДІВАННЯ ТЕОРЕМА 5.1. (Властивості математичного сподівання). 1. Математичне сподівання від сталої величини С дорівнює самій сталій:
М(С) = С. 2. Сталу величину можна виносити за знак математичного сподівання, тобто якщо - випадкова величина, а С - стала, тоді М(С) = С. 3. Нехай - дискретна випадкова величина, математичне сподівання якої означене. Тоді ДОВЕДЕННЯ: 1. Справді, сталу С можна розглядати як випадкову величину, що з імовірністю, яка дорівнює одиниці, набуває значення С, а тому М(С) = С 1 = С. 2. На підставі означень 5.1 та 5.2, згідно властивостей суми та інтегралу маємо: - для дискретної випадкової величини
- для неперервної:
3. Зауважимо, що коли Нехай дискретна випадкова величина має розподіл :
Тоді випадкова величина : Оскільки ряд
Для неперервної випадкової величини:
Зауважимо, що коли випадкова величина а;b, то М() а;b, а саме: математичне сподівання випадкової величини обов'язково міститься всередині інтервалу а;b, яке являє центр розподілу цієї величини.
ТЕОРЕМА 5.2. Нехай , - дискретні випадкові величини, математичні сподівання яких скінченні. Тоді + має скінчене математичне сподівання і
ОЗНАЧЕННЯ 5.3. Дві дискретні випадкові величини , з розподілами : та : називають незалежними, якщо події незалежні для будь-яких
ТЕОРЕМА 5.3. Якщо математичними сподіваннями, то випадкова величина (дискретна) математичне сподівання
ДОВЕДЕННЯ: Нехай Випадкова величина приймає значення
Оскільки ряди
ДИСПЕРСІЯ ТА СЕРЕДНЄ КВАДРАТИЧНЕ ВІДХИЛЕННЯ
Розглянемо випадкові величини, які мають різні закони розподілу, але їх, математичні сподівання однакові. Отже, математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню М() може відповідати безліч випадкових величин, які будуть різнитися не лише можливими значеннями, а й характером розподілу та самою природою можливих значень. Приклад 5.9.
Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією. Щоб визначити дисперсію, розглянемо випадкову величину:
Математичне сподівання випадкової величини М(
Отже, відхилення не може бути мірою розсіювання випадкової величини.
ОЗНАЧЕННЯ 5.6. Дисперсією випадкової величини називається математичне сподівання квадрата відхилення цієї величини від свого математичного сподівання
D() = М[ - М ()]2 .
Для дискретної випадкової величини дисперсія обчислюється за формулою:
Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, алеув квадраті. Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Тому разом з дисперсією, як мірою розсіювання випадкової величини (для вимірювання розсіювання) уводиться також числова характеристика, яку називають середнє квадратичне відхилення.
Середнім квадратичним відхиленням випадкової величини називають корінь квадратний з дисперсії: 5.1.5 ВЛАСТИВОСТІ ДИСПЕРСІЇ ТЕОРЕМА 5.4. (Властивості дисперсії). 1. Для будь якої випадкової величини вірно D 0. 2. Якщо С - стала величина, то D( C ) = 0. 3. Якщо c - стала величина, то D(c) = c2 D. 4. Якщо a i b - сталі величини, то D(a + b) = a2 D. 5. Якщо випадкові величини і незалежні, тоді D( ) = D + D.
ДОВЕДЕННЯ: Властивості 1 - 5 можна довести згідно властивостей математичного сподівання. Справді: 1. D() = М[ - М ()]2 = М(
2. D(С) = М[С - М (С)]2 = М[С - С]2 = М(0) = 0.
3. D(c) = М[c - М (c)]2 = М[c - cМ ()]2 =М[c( - М ())]2 = = c2М[ - М ()]2 = c2D().
4. Згідно властивостей 2 та 3 маємо:
D(a + b) = М[а + b - М(а + b)]2 = М[а + b - аМ() - b]2 = = М[а( - М()]2 = a2М[ - М()]2 = a2 D.
6. Зауважимо, що дисперсію, спідручніше, можна обчислити за формулою: 7. D = M2 - (M)2. (*) Справді,
D = M(- M)2 = M[2 - 2M + (M)2] = M2 - 2MM + (M)2] = = M2 - (M)2.
маємо
D( + ) = M[( + ) - M ( + )]2 = M[( - M) +( - M)]2 = = M( - M)2 +M( - M)2 + 2 М[( - M) ( - M)],
але випадкові величини і незалежні, тоді ( - M) і ( - M) теж незалежні, і тоді М[( - M) ( - M)] = М( - M) М( - M) = 0. Звідси маємо
D( + ) = M( - M)2 +M( - M)2 = D + D; D( - ) = D( + (-)) = D + D(-) = D + (-1)2 D D + D.
Нехай потрібно дослідити яку-небудь ознаку, характерну великій групі однотипних елементів (наприклад, міцність зразків сплаву, відхилення розмірів виготовлених деталей від номінального розміру, тощо). Сукупність значень ознаки всіх Число Звичайно, на практиці неможливо, або й економічно невигідно обстежити всю генеральну сукупність. Тоді із всієї сукупності елементів випадковим чином вибирають обмежену кількість елементів, які і вивчають. Вибірковою сукупністю або вибіркою називається сукупність випадково відібраних елементів. Вибірковий метод полягає в тому, що з генеральної сукупності обсягу 1.1. Статистичний розподіл вибірки Нехай в результаті проведення досліду з генеральної сукупності зроблена вибірка обсягу Значення
або таблиці відносних частот
Якщо ознака
При цьому весь діапазон зміни варіант від Сукупність значень варіант і відповідних їм частот (або відносних частот) називають статистичним розподілом вибірки. Приклад 1. Задано розподіл вибірки Записати розподіл відносних частот. Розв’язання. Обсяг вибірки Шуканий розподіл відносних частот має вигляд
або остаточно
Варто зауважити, що в теорії ймовірностей під розподілом розуміємо відповідність між можливими значеннями випадкової величини і їх ймовірностями, а в математичній статистиці під розподілом розуміємо відповідність між спостережуваними значеннями (варіантами) і їх частотами (або відносними частотами).
Статистичні оцінки параметрів розподілу Нехай нам потрібно вивчити кількісну ознаку генеральної сукупності. Припустимо, що з теоретичних міркувань ми допускаємо певний вид розподілу ознаки, наприклад розподіл Пуассона. Цей розподіл визначається параметром Розглядаючи значення Нехай θ - невідомий параметр теоретичного розподілу. Задача оцінювання параметра полягає в побудові наближеної формули θ де функція θ*
незміщеною називається оцінка, математичне сподівання якої дорівнює оцінюваному параметру
Оцінка θ* називається спроможною, якщо вона збігається за ймовірністю до оцінюваного параметра θ, тобто
Для виконання цієї умови достатньо, щоб дисперсія оцінки
Оцінки, що мають властивості незміщеності і спроможності, при обмеженій кількості дослідів можуть відрізнятися дисперсіями. Очевидно, що чим менша дисперсія оцінки, тим менша ймовірність грубої похибки при визначенні наближеного значення параметра. Тому необхідно, щоб дисперсія оцінки була мінімальною
Остання умова і визначає ефективність оцінки.
Критерій узгодженості Пірсона - один з найвідоміших критеріїв χ2, тому його часто і називають просто "критерій хі-квадрат". Використовується для перевірки гіпотези про закон розподілу. Ґрунтується на групованих даних. Область значень передбачуваного розподілу Нехай X=(X1,…, Xn) — вибірка з розподілу і через pj > 0 — теоретичну ймовірність Етапи перевірки статистичних гіпотез Формулювання основної гіпотези H0 і конкуруючої гіпотези H1. Гіпотези повинні бути чітко формалізовані в математичних термінах. Задання вірогідності α, що називається рівнем значущості і що відповідає помилкам першого роду, на якому надалі і буде зроблений висновок про правдивість гіпотези. Розрахунок статистики φ критерію такий, що: її величина залежить від початкової вибірки по її значенню можна зробити висновки про істинність гіпотези H0; сама статистика φ повинна підкорятися якомусь невідомому закону розподілу, так як сама φ є випадковою в силу випадковості Побудова критичної області. З області значень φ виділяємо підмножину Висновок про істинність гіпотези. Спостережувані значення вибірки підставляються в статистику φ і по попаданню (або непопаданню) в критичну область Областю значень функції (відображення) Множина Y зовсім не обов'язково збігається з областю значень f. У загальному випадку, B є лише підмножиною Y.
Метод найменших квадратів — метод знаходження наближеного розв'язку надлишково-визначеної системи. Часто застосовується врегресійному аналізі. На практиці найчастіше використовується лінійний метод найменших квадратів, що використовується у випадкусистеми лінійних рівнянь. Зокрема важливим застосуванням у цьому випадку є оцінка параметрів у лінійній регресії, що широко застосовується у математичній статистиці і економетриці. Лінійний випадок Для надлишково-визначеної системи m лінійних рівнянь з n невідомими
чи в матричній формі запису:
зазвичай не існує точного розв'язку, і потрібно знайти такі β, які мінімізують наступну норму:
Такий розв'язок завжди існує і він є єдиним:
хоч дана формула не є ефективною через необхідність знаходити обернену матрицю Якщо дано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку економетричну модель, яка б найкраще описувала існуючу залежність. Одним з методів є лінійна регресія. Лінійна регресія передбачає побудову такої прямої лінії, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю пряму одержуємо значення прогнозу. Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої.
|




 де
де
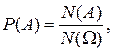 (1)
(1) (на прямій – довжину, на площині – площу, у просторі – об’єм). Розглянемо систему F підмножин простору Ω, які мають міру. Відомо, що вони утворюють σ-алгебру. Множини з F назвемо випадковими подіями. Якщо експеримент має властивість симетрії щодо елементарних результатів (наприклад, деякий „точковий” об’єкт “навмання” кидаємо в межах області), то всі елементарні події „рівноправні”, тож природно припустити, що ймовірність попадання елементарної події ω у будь-яку частину Ω пропорційна мірі цієї частини і не залежить від її розташування і форми. Тоді ймовірність будь-якої події
(на прямій – довжину, на площині – площу, у просторі – об’єм). Розглянемо систему F підмножин простору Ω, які мають міру. Відомо, що вони утворюють σ-алгебру. Множини з F назвемо випадковими подіями. Якщо експеримент має властивість симетрії щодо елементарних результатів (наприклад, деякий „точковий” об’єкт “навмання” кидаємо в межах області), то всі елементарні події „рівноправні”, тож природно припустити, що ймовірність попадання елементарної події ω у будь-яку частину Ω пропорційна мірі цієї частини і не залежить від її розташування і форми. Тоді ймовірність будь-якої події  F можна обчислити, користуючись таким означенням.
F можна обчислити, користуючись таким означенням. до міри
до міри  тобто
тобто 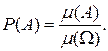
 (бо сума всіх ймовірностей елементарних подій за аксіомою 2 повинна дорівнювати 1). Тодіймовірність довільної події А легко визначити: досить підрахувати кількість елементарних подій з яких складається подія А (цю кількість позначимо через m) і поділити на кількість усіх елементарних подій. Отже,
(бо сума всіх ймовірностей елементарних подій за аксіомою 2 повинна дорівнювати 1). Тодіймовірність довільної події А легко визначити: досить підрахувати кількість елементарних подій з яких складається подія А (цю кількість позначимо через m) і поділити на кількість усіх елементарних подій. Отже, .
. ,
,
 (А, В – несумісні), Þ
(А, В – несумісні), Þ – ймовірність суми = сумі ймовірностей.
– ймовірність суми = сумі ймовірностей.

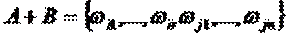 ,
,

 ,
,  .
. .
.
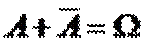



 Якщо попадаємо в А, то ми автоматично
Якщо попадаємо в А, то ми автоматично




 ,
, 

 — фіксований ймовірнісний простір. Нехай
— фіксований ймовірнісний простір. Нехай  дві випадкової події, причому
дві випадкової події, причому  . Тоді умовною ймовірністю події A при умові події Bназивається
. Тоді умовною ймовірністю події A при умові події Bназивається

 , то умовна ймовірність, строго кажучи, не визначена. Проте іноді умовляються вважати її в цьому випадку рівною нулю .
, то умовна ймовірність, строго кажучи, не визначена. Проте іноді умовляються вважати її в цьому випадку рівною нулю . , задана формулою
, задана формулою
 , таких що
, таких що  . Хай
. Хай  подія, що цікавить нас. Тоді
подія, що цікавить нас. Тоді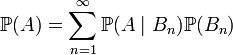 .
. .
. ,
,
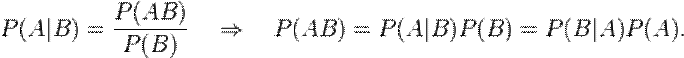
 — ймовірність настання події B, що залежить від гіпотез Ai, якщо відомі їх ступені достовірності.
— ймовірність настання події B, що залежить від гіпотез Ai, якщо відомі їх ступені достовірності.
 (це читач може довести сам).
(це читач може довести сам). . Усього таких подій можна нарахувати стільки, скільки утворити різних послідовностей довжини n, містять x цифр " 1 " і n–x цифр " 0 " . Таких послідовностей виходить стільки, скількома способами можна розмістити x цифр " 1 " (чи n–x цифр " 0 " ) на n місцях, тобто кількість цих послідовностей одно
. Усього таких подій можна нарахувати стільки, скільки утворити різних послідовностей довжини n, містять x цифр " 1 " і n–x цифр " 0 " . Таких послідовностей виходить стільки, скількома способами можна розмістити x цифр " 1 " (чи n–x цифр " 0 " ) на n місцях, тобто кількість цих послідовностей одно 

 щодо одного испытании.
щодо одного испытании.
 , "значення" якої
, "значення" якої  утворюють множину
утворюють множину  елементарних подій, або, іншими словами, позначають точки в просторі вибірок. Відповідний розподіл імовірностей називається розподілом випадкової величини
елементарних подій, або, іншими словами, позначають точки в просторі вибірок. Відповідний розподіл імовірностей називається розподілом випадкової величини  . [2]
. [2] елементарних подій являє собою можливі значення випадкової величини
елементарних подій являє собою можливі значення випадкової величини  , тобто, вона визначається шляхом зіставлення кожної елементарної події з деяким дійсним числом. Більш формально:
, тобто, вона визначається шляхом зіставлення кожної елементарної події з деяким дійсним числом. Більш формально: називається випадковою величиною, якщо
називається випадковою величиною, якщо  , де
, де  -- σ-алгебра Борелевих множин на
-- σ-алгебра Борелевих множин на  .
. . Система рівнянь:
. Система рівнянь:
 та
та  .
. ,
,  і т. д. призначаються визначені ймовірності.
і т. д. призначаються визначені ймовірності. ,
,  , …,
, …,  виконується рівність:
виконується рівність:

 ;
;  — граничні значення нормованої величини
— граничні значення нормованої величини  ;
; — це середнє значення величини
— це середнє значення величини  — cтандартне відхилення цієї величини.
— cтандартне відхилення цієї величини. ,
, — невід'ємна інтегровна за Лебегом функція, яка називається функцією густини імовірності випадкової величини ξ.
— невід'ємна інтегровна за Лебегом функція, яка називається функцією густини імовірності випадкової величини ξ.

 , де f(t) — характеристична функція випадкової величини ξ.
, де f(t) — характеристична функція випадкової величини ξ. ;
; .
.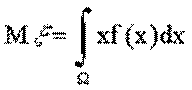 ,
, .
. .
. , де a та b - постійні.
, де a та b - постійні.

 - дискретні випадкові величини і
- дискретні випадкові величини і  - борелівська функція n змінних, то суперпозиція
- борелівська функція n змінних, то суперпозиція  - теж дискретна випадкова величина.
- теж дискретна випадкова величина. .
. має розподіл
має розподіл



 .
.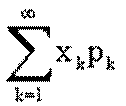 абсолютно збігається, тому ряд
абсолютно збігається, тому ряд теж абсолютно збігається, і
теж абсолютно збігається, і




 та
та 
 , тобто
, тобто
 незалежні дискретні випадкові величини зі скінченими
незалежні дискретні випадкові величини зі скінченими має скінчене
має скінчене .
. мають розподіли як в означенні 5.3.
мають розподіли як в означенні 5.3. (не всі, можливо, рівні) з ймовірностями
(не всі, можливо, рівні) з ймовірностями (з огляду на незалежність
(з огляду на незалежність  ).
). та
та  абсолютно збіжні, то подвійний ряд
абсолютно збіжні, то подвійний ряд  теж абсолютно збіжний, і тоді
теж абсолютно збіжний, і тоді .
. - відхилення випадкової величини від свого математичного сподівання
- відхилення випадкової величини від свого математичного сподівання  = ( - М ()).
= ( - М ()). завжди дорівнює нулю. Справді,
завжди дорівнює нулю. Справді, ) = М( - М ()) = M() - M(М ()) = M() - M() = 0.
) = М( - М ()) = M() - M(М ()) = M() - M() = 0.


 ) 0, так як
) 0, так як  елементів даного типу називається генеральною сукупністю.
елементів даного типу називається генеральною сукупністю. , де
, де  і визначаються характеристики вибірки, які приймаються за наближене значення відповідних характеристик генеральної сукупності.
і визначаються характеристики вибірки, які приймаються за наближене значення відповідних характеристик генеральної сукупності. - дискретна випадкова величниа, причому значення
- дискретна випадкова величниа, причому значення  спостерігалось
спостерігалось  разів, тобто
разів, тобто 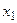 спостерігалось
спостерігалось  разів,
разів,  -
-  разів, …,
разів, …,  -
-  разів, і
разів, і  (обсягу вибірки).
(обсягу вибірки). - відносними частотами. Результати досліду зручно представити у вигляді таблиці частот
- відносними частотами. Результати досліду зручно представити у вигляді таблиці частот
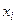

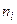








 =
=  до
до  =
=  розбивають на 10-20 частинних інтервалів з межами
розбивають на 10-20 частинних інтервалів з межами  ,
,  ,…,
,…,  і підраховують частоту
і підраховують частоту  попадання в
попадання в  -й частинний інтервал. Аналогічно будується інтервальна таблиця відносних частот.
-й частинний інтервал. Аналогічно будується інтервальна таблиця відносних частот. .
. .
.

 , який треба оцінити, виходячи з даних вибірки
, який треба оцінити, виходячи з даних вибірки  .
. як незалежні випадкові величини
як незалежні випадкові величини  , приходимо до висновку, що знайти статистичну оцінку невідомого параметра розподілу означає знайти функцію від випадкових величин, яка й буде наближеним значенням параметра.
, приходимо до висновку, що знайти статистичну оцінку невідомого параметра розподілу означає знайти функцію від випадкових величин, яка й буде наближеним значенням параметра. θ*
θ*  , (2)
, (2)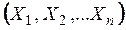 - статистика - теж є випадковою величиною, закон розподілу якої залежить як від закону розподілу випадкових величин
- статистика - теж є випадковою величиною, закон розподілу якої залежить як від закону розподілу випадкових величин  , так і від кількості дослідів. Значення функції θ*
, так і від кількості дослідів. Значення функції θ*  в наближеній рівності (2) називається оцінкою параметра θ. Для того, щоб оцінка θ* мала практичну цінність, вона повинна мати такі властивості:
в наближеній рівності (2) називається оцінкою параметра θ. Для того, щоб оцінка θ* мала практичну цінність, вона повинна мати такі властивості: . незміщеність
. незміщеність . (3)
. (3) . спроможність (обгрунтованість)
. спроможність (обгрунтованість) ,
, 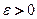 . (4)
. (4) при
при  , тобто
, тобто (це випливає із нерівності Чебишова).
(це випливає із нерівності Чебишова). . ефективність .
. ефективність . (5)
(5) ділять на деяке число інтервалів.
ділять на деяке число інтервалів. . Перевіряється проста гіпотеза
. Перевіряється проста гіпотеза  проти складної альтернативи
проти складної альтернативи 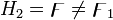 .
.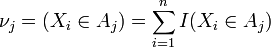 ,
, попадання в інтервал Aj випадкової величини з розподілом
попадання в інтервал Aj випадкової величини з розподілом  .
. (1).
(1). ;
; .
. таких значень, по яким можна судити про суттєвість розбіжностей з припущенням. Її розмір вибирається таким чином, щоб виконувалась рівність
таких значень, по яким можна судити про суттєвість розбіжностей з припущенням. Її розмір вибирається таким чином, щоб виконувалась рівність  . Ця множина
. Ця множина  називається множина B⊂Y така, що f(X) = B.
називається множина B⊂Y така, що f(X) = B.



