 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Основні поняття алгебри логіки
Логічною основою комп’ютера є алгебра логіки, яка розглядає логічні операції над висловлюваннями. Алгебра логіки – це розділ математики, що вивчає висловлювання, що розглядаються зі сторони їх логічних значень (істини або хибності) і логічних операцій над ними. Логічне висловлювання – це будь-яке розповідне речення, стосовно якого можна однозначно сказати, чи є воно істинним або хибним.
Приклад 2.1. «3 – просте число» є висловлюванням, оскільки воно є істинним. Не будь-яке речення є логічним висловлюванням.
Висловлювальна форма – це розповідне речення, яке прямо або опосередковано містить хоча б одну змінну і стає висловлюванням, коли всі змінні заміщаються своїми значеннями.
Приклад 2.2 «x+2>5» - висловлювальна форма, яка при x>3 є істинною, а в протилежному випадку хибною.
Алгебра логіки розглядає будь-яке висловлювання з однієї точки зору – є воно істинним або хибним. Слова і словосполучення «не», «і», «або», «якщо ..., то», «тоді і тільки тоді» та інші дозволяють з вже заданих висловів будувати нові висловлювання. Такі слова і словосполучення називаються логічними зв'язками. Висловлювання, утворені з інших висловлювань за допомогою логічних зв'язок, називаються складними (складними). Висловлювання, які не є складовими, називаються елементарними(простими).
Приклад. Вислів «Число 6 ділиться на 2» - просте висловлювання. Вислів «Число 6 ділиться на 2, і число 6 ділиться на 3» - складене висловлювання, утворене з двох простих за допомогою логічної зв'язки «і». Істинність або хибність складових висловлювань залежить від істинності чи хибності елементарних висловлювань, з яких вони складаються. Щоб звертатися до логічних висловлювань, їм призначають імена.
Приклад 2.3. Позначимо через А просте висловлювання «число 6 ділиться на 2», а через В просте висловлювання «число 6 ділиться на 3». Тоді складене висловлювання «Число 6 ділиться на 2, і число 6 ділиться на 3» можна записати як «А і В». Тут «і» - логічна зв'язка, А, В - логічні змінні, які можуть приймати тільки два значення - «істина» або «брехню», що позначаються, відповідно, «1» і «0». Кожна логічна зв'язка розглядається як операція над логічними висловленнями і має свою назву та позначення (табл. 1).
Таблиця 2.1
НЕ Операція, що виражається словом «не», називається запереченням і позначається рискою над висловлюванням (або знаком ). Висловлювання А істинне, коли A помилкове, і помилкове, коли A істинне.
Приклад 2.4. Нехай А = «Сьогодні похмуро», тоді А = «Сьогодні не похмуро».
І Операція, що виражається зв'язкою «і», називається кон'юнкцією (лат. conjunctio - з'єднання) або логічним множенням і позначається крапкою « • » (може також позначатися знаками
Приклад 2.5. Вислів «Число 6 ділиться на 2, і число 6 ділиться на 3» - істинний, а вислів «Число 6 ділиться на 2, і число 6 більше 10» - хибний.
АБО Операція, що виражається зв'язкою «або» (в прямому сенсі цього слова), називається диз'юнкцією (лат. disjunctio - поділ) або логічним додаванням і позначається знаком
Приклад 2.6. Вислів «Число 6 ділиться на 2 або число 6 більше 10» - істинний, а вислів «Число 6 ділиться на 5 або число 6 більше 10» - хибний.
АБО ... АБО Операція, що виражається зв'язками «Або ... або», називається виключаюче АБО чи додавання по модулю 2 і позначається XOR або Приклад 2.7. Вислів «Число 6 або непарне або ділиться без залишку на 2» є істинним, а вислів «Або число 6 парне або число 6 ділиться на 3» - помилковий, так як істинні обидва висловлювання, що входять в нього.
Зауваження. Імплікацію можна виразити через диз'юнкцію і заперечення:
Виключаюче АБО можна виразити через заперечення, диз'юнкцію і кон'юнкцію:
Висновок. Операцій заперечення, диз'юнкції і кон'юнкції достатньо, щоб описувати й обробляти логічні висловлювання. Порядок виконання логічних операцій задається круглими дужками. Але для зменшення числа дужок домовилися вважати, що спочатку виконується операція заперечення («не»), потім кон'юнкція («і»), після кон'юнкції – диз'юнкція («або») і виключаюче або.
За допомогою логічних змінних і символів логічних операцій будь-яке висловлювання можна формалізувати, тобто замінити логічною формулою (логічним вираженням).
Логічна формула – це символічний запис висловлювання, що складається з логічних величин (констант або змінних), об'єднаних логічними операціями (зв'язками). Логічна функція – це функція логічних змінних, яка може приймати тільки два значення: 0 або 1. У свою чергу, сама логічна змінна (аргумент логічної функції) теж може приймати тільки два значення: 0 або 1.
Приклад 2.8.
Значення логічної функції для різних поєднань значень вхідних змінних - або, як це інакше називають, наборів вхідних змінних - звичайно задаються спеціальною таблицею. Така таблиця називається таблицею істинності(табл. 2.1).
Таблиця 2.2. Таблиця істинності основних логічних операцій
Спираючись на дані таблиці істинності основних логічних операцій можна складати таблиці істинності для більш складних формул.
Алгоритм побудови таблиць істинності для складних виразів:
1. Визначити кількість рядків: кількість рядків = 2n + рядок для заголовка; n - кількість простих висловлювань. 2. Визначити кількість стовпців: кількість стовпців = кількість змінних + кількість логічних операцій; визначити кількість змінних (простих виразів); визначити кількість логічних операцій і послідовність їх виконання.
Приклад 2.9. Скласти таблицю істинності для формули І-НЕ, яку можна записати так:
Рішення: Визначити кількість рядків: На вході два простих висловлювання: А і В, тому n = 2 і кількість рядків = 22 +1 = 5. 2. Визначити кількість стовпців: Вираз складається з двох простих виразів (A і B) і двох логічних операцій (1 інверсія, 1 кон'юнкція), тобто кількість стовпців таблиці істинності = 4. 3. Заповнити стовпці з урахуванням таблиць істинності логічних операцій (табл. 2.3).
Таблиця 2.3. Таблиця істинності для логічної операції
Подібним чином можна скласти таблицю істинності (табл. 2.4) для формули АБО-НЕ, яку можна записати так:
Таблиця 2.4. Таблиця істинності для логічної операції
Примітка. І-НЕ називають також «штрих Шеффера» (позначають |) або «антикон'юнкція»; АБО-НЕ називають також «стрілка Пірса» (позначають ↓) або «антидиз'юнкція». Приклад 2.10. Скласти таблицю істинності логічного виразу Рішення: 1. Визначити кількість рядків: На вході два простих висловлювання: А і В, тому n = 2 і кількість рядків = 22 +1 = 5. 2. Визначити кількість стовпців: Вираз складається з двох простих виразів (A і B) і п'яти логічних операцій (2 інверсії, 2 кон'юнкції, 1 диз'юнкція), тобто кількість стовпців таблиці істинності = 7. Спочатку виконуються операції інверсії, потім кон'юнкції, в останню чергу операція диз'юнкції. 3. Заповнити стовпці з урахуванням таблиць істинності логічних операцій (табл. 2.5).
Таблиця 2.5. Таблиця істинності для логічної операції
Логічні формули можна також представляти за допомогою мови логічних схем. Існує три базових логічних елемента, які реалізують три основні логічні операції: - логічний елемент «І» - логічне множення - кон'юнктор; - логічний елемент «АБО» - логічне додавання - диз'юнктор; - логічний елемент «НЕ» - інверсію - інвертор.
Рисунок 2.1 – Базові логічні елементи
Оскільки будь-яка логічна операція може бути представлена у вигляді комбінації трьох основних, будь-які пристрої комп'ютера, що виконують обробку або зберігання інформації, можуть бути зібрані з базових логічних елементів, як з "цеглинок". Логічні елементи комп'ютера оперують з сигналами, що представляють собою електричні імпульси. Є імпульс – логічний зміст сигналу – 1, немає імпульсу – 0. На входи логічного елемента надходять сигнали-значення аргументів, на виході з'являється сигнал-значення функції. Перетворення сигналу логічним елементом задається таблицею станів, яка фактично є таблицею істинності, відповідної логічної функції, тільки представлена в формі логічних схем. У такій формі зручно зображувати ланцюжки логічних операцій і виробляти їх обчислення.
Алгоритм побудови логічних схем: 1. Визначити число логічних змінних. 2. Визначити кількість логічних операцій і їх порядок. 3. Зобразити для кожної логічної операції відповідний їй логічний елемент. 4. З'єднати логічні елементи в порядку виконання логічних операцій.
Приклад 2.11. За заданою логічною функцією Рішення: 1. Число логічних змінних = 2 (A і B). 2. Кількість операцій = 5 (2 інверсії, 2 кон'юнкції, 1 диз'юнкція). Спочатку виконуються операції інверсії, потім кон'юнкції, в останню чергу операція диз'юнкції. 3. Схема буде містити 2 інвертора, 2 кон'юнктора і 1 диз'юнктор. 4. Побудову треба починати з логічної операції, яка повинна виконуватися останньою. В даному випадку такою операцією є логічне додавання, отже, на виході повинен бути диз'юнктор. На нього сигнали подаються з двох кон'юнкторов, на які, в свою чергу, подаються один вхідний сигнал нормальний та один інвертований (з інверторів).
Рисунок 2.2 – Приклад побудови логічних схем
|






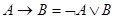 .
. .
. – логічна функція двох змінних A і B.
– логічна функція двох змінних A і B.



 .
.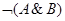
 .
.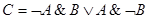 .
.



 побудувати логічну схему.
побудувати логічну схему.