ПОЗНАВАТЕЛЬНОЕ

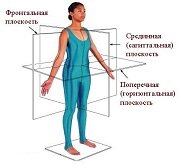
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Скалярное произведение векторов

Векторы

Физические законы обладают двумя свойствами, которые называют инвариантностью (или симметрией) относительно перемещений и поворотов координатных осей. Эти свойства так важны, что для учета их при изучении физических законов была разработана специальная математическая техника, называемая векторным анализом.

Важно различать физические величины двух типов. Величины первого типа характеризуются только численным значением (например, температура, количество предметов и т.д.) - это скаляры. Другие величины - векторы - характеризуются не только численным значением, но и направлением в пространстве. Численные значения физических величин и их направление в каждой точке пространства не зависят от выбора системы координат. Например, перемещение из начала координат в точку Р(х,у,z) (шаг в пространстве, который имеет определенную длину и направление).

Вектор определяется тремя числами - его проекциями на координатные оси. Например, перемещение из начала координат в точку Р(х,у,z) можно описать тремя числами х,у,z. Но можно использовать для этой цели один - единственный символ r (радиус-вектор). Радиус-вектор широко используется для задания положения точки в пространстве относительно выбранной системы координат. Символ r задается не только тремя числами х,у,z, но и числами в другой системе координат. Т.е. мы используем один и тот же символ в качестве представителя трех чисел в одной системе координат и делаем его представителем второго набора чисел, если захотим сменить систему координат. Это удобно потому, что не придется изменять форму уравнений при изменении системы координат. Очевидно, что проекции вектора при изменении системы координат должны измениться по строго определенным законам, таким же, как и тройки чисел х,у,z и . Только в этом случае, проекции вектора отображают один и тот же объект во всех системах координат. Для шага в пространстве нам очевидно, что это один и тот же объект во всех системах координат (шаг имеет определенную длину и направление в пространстве не зависящие от выбора системы координат). А бывают случаи, когда требуется специальное исследование, устанавливающее, по каким законам изменяются тройки чисел, характеризующие величину, при изменении системы координат, заранее это не очевидно. Если эти законы такие же, как и для тройки чисел х,у,z, то величине присваивается статус вектора (объекта, не зависящего от выбора системы координат).

Определим вектор математически как величину, определяемую тремя числами, которые преобразуются при изменении системы координат так же, как и координаты. То, что физические соотношения между какими-то величинами можно выразить в форме векторных уравнений отражает тот факт, что эти соотношения верны в любой системе координат.

Часто бывает удобно изобразить вектор в виде стрелки, указывающей направление. Стрелка преобразуется по тем же законам, что и шаг в пространстве. Изобразив ее, не нужно заботиться о координатных осях.

Внимание!

Вектор обозначается жирным шрифтом (например, r, v, a). В рукописях (конспекте и т.п.)вектор обозначается стрелкой, или черточкой над буквой.

Полезно увидеть законы преобразования хотя бы в упрощенном частном случае. Например, одна система координат повернута относительно другой вокруг оси z на угол q. Начало координат в обеих системах совпадает.

Векторная алгебра

Опишем законы, или правила, регулирующие возможные сочетания различных векторов. Прежде всего, изучим сумму двух векторов. Пусть векторы а и b задаются в какой-нибудь системе координат составляющими a_x, a_y, a_z и b_x, b_y, b_z. Предположим, что кому-то пришло в голову составить три числа a_x + b_x, a_y + b_y, a_z + b_z. Получим ли мы в результате вектор? Вектор образуют не любые три числа! Чтобы задать вектор, мы должны связать заданные нам три числа с координатной системой так, чтобы при повороте координатных осей эти числа преобразовывались по описанным ранее правилам. Таким образом, мы должны выяснить, во что превращаются числа a_x + b_x, a_y + b_y, a_z + b_z , если известно, что при изменении системы координат числа a_x, a_y, a_z переходят в , а b_x, b_y, b_z переходят в ? Получим ли мы после поворота координатных осей числа ? Ответ, конечно, будет утвердительным потому, что уравнения для закона преобразования (1) линейны. «Складывая» векторыа и bпо только что описанному правилу, мы получим новый векторс. Мы запишем это так:

c = а + b.

Вектор с обладает свойством:

с = b + a;

это легко проверить, написав составляющие вектора с. Кроме того,

a + (b + c) = (a + b) + c.

Векторы можно складывать в любом порядке.

Каков геометрический смысл a + b? Как будет выглядеть вектор с, если мы, скажем, изобразим a и bс помощью стрелок? Ответ на этот вопрос дает рисунок. Мы видим, что прибавить составляющие вектора b к составляющим вектора а проще всего, приложив соответствующим образом прямоугольник, определяемый составляющими b, к такому же прямоугольнику, определяемому составляющими а. Поскольку а и b хорошо подогнаны к своим прямоугольникам, то это все равно, что поставить векторb «ногами» на «голову» вектору а. Стрелка, соединяющая «ноги» вектора а и «голову» вектора b, и будет вектором с. Можно поступить иначе: поставить «ноги» а на «голову» b. Вспомнив геометрические свойства параллелограмма, можно убедиться в том, что мы снова получим тот же вектор с. Заметим, что, ставя векторы друг на друга, мы складываем их без помощи координатных осей.

Предположим, что мы умножили вектор а на число a. Что нужно понимать под таким произведением? Договоримся понимать под этим вектор с компонентами aa_x, aa_y, aa_z. Легко увидеть из законов преобразования (1), что это действительно вектор.

Рассмотрим теперь вычитание векторов. Можно определить вычитание тем же способом, что и сложение, но вместо того, чтобы складывать, будем вычитать составляющие. Можно также определить вычитание как сложение с отрицательным вектором (-b). Результат буде тот же.

Вычитание векторов показано на рисунке. На этом чертеже изображено d = a – b.

Скалярное произведение векторов

Легко понять, что длина шага в пространстве одинакова во всех координатных схемах. Следовательно, если какому-то шагу r соответствуют составляющие х,у,z в одной системе координат и составляющие в другой системе, то расстояние одно и тоже в обеих системах:

Легко доказать с помощью законов преобразования (1), что эти расстояния равны. Удобней сравнивать квадраты расстояний:

Незаметно мы получили новый тип величин. Мы можем построить функцию координат х,у,z, называемую скалярной функцией, - величину, которая не имеет направления, и одинакова во всех системах координат. Из вектора можно построить скаляр. Правило для этого мы уже нашли: нужно возвести в квадрат каждую из составляющих вектора и сложить их. Определим теперь новую величину, которую обозначим а×а. Это не вектор, а скаляр; это число, одинаковое во всех координатных системах и определяемое как сумма квадратов трех составляющих вектора:

(2)

Вы спросите: «В какой системе координат?» Но раз это число не зависит от системы координат, то ответ одинаков в любой системе координат. Мы имеем дело с новым видом величины, с инвариантом, или скаляром, полученным «возведением вектора в квадрат». Если теперь определить, исходя из векторов a и b, величину

(3)

то можно убедиться, что эта величина совпадает в штрихованной и нештрихованной системах координат. Чтобы доказать это, заметим, что это верно для величин а×а, b×b, c×c, где c = a + b. Мы уже знаем, что инвариантом является сумма квадратов:

Раскроем скобки в обеих сторонах этого уравнения. Перекрестные произведения дадут нам выражения типа (3), а суммы квадратов составляющих a и b – выражения типа (2). Инвариантность слагаемых типа (2) приводит к инвариантности перекрестных произведений типа (3).

Величина называется скалярным произведением двух векторов a и b и имеет много интересных и полезных свойств.

Например, легко доказать, что

Есть еще очень простой геометрический способ вычисления , при котором не надо определять составляющих векторов; просто есть произведение длин векторов a и bна косинус угла между ними. Почему? Предположим, что мы выбрали такую систему координат, в которой вектор а направлен вдоль оси х; в этом случае вектор а имеет единственную ненулевую составляющую а_х, которая равна длине вектора а. Таким образом, уравнение (3) сводится в этом случае к , что равно произведению длины вектора а на составляющую вектора b по направлению а, которая в свою очередь равна b cosq, т.е.

Таким образом, в этой частной системе координат мы доказали, что есть произведение длин векторов a и bна косинус угла между ними. Но если это верно в одной системе координат, то это верно и во всех системах, потому что не зависит от выбора системы координат.

Что хорошего может дать нам эта новая величина? Нужно ли физику скалярное произведение? Да, оно необходимо ему постоянно. С примерами этого мы неоднократно столкнемся. Скалярное произведение широко используется не только в физике и математике, а и во многих других науках.

Удобно определить еще одно произведение двух векторов, которое называется векторным произведением и записывается в виде . Понятие векторного произведения естественным образом появляется при анализе вращательного движения. Приведем соответствующую выдержку из раздела «Механика».

Векторное произведение

Операция с двумя векторами a и b, позволяющая получить из них новый вектор с, которая носит название «векторное произведение», обозначается обычно двумя способами:

с = а´b = [a, b],

что расшифровывается:

c_x = a_yb_z - a_zb_y

c_y = a_zb_x - a_xb_z

c_z = a_xb_y - a_yb_x

Свойства векторного произведения

а´b = -b´a

Отсюда:

а´а = 0

Результатом векторного произведения есть вектор, который перпендикулярен обоим перемножаемым векторам: с^а, с^b. Доказательством является равенство нулю скалярных произведений с×а и с×b (скалярные произведения можно расписать как сумму произведений одноименных проекций векторов).

Модуль векторного произведения равен произведению модулей векторов на синус угла между ними: ÷а´b ê= а b sina. Это правило легко доказывается путем вычисления результата векторного произведения через проекции векторов для простейшего частного случая: вектор а смотрит из начала координат в направлении оси х (а_y и a_z = 0; a_x = a), вектор b -расположен в плоскости ху (b_z = 0). Поскольку результат векторного произведения не зависит от выбора системы координат (это свойство любого вектора, для этого они и придуманы), правило можно распространить на произвольную систему координат.

Способ определения направления вектора, являющегося результатом векторного произведения: если вращать вектор а (первый из перемножаемых векторов) по направлению к вектору b (второй из перемножаемых векторов), то вектор c = а´b будет направлен в сторону поступательного движения, связанного с этим вращением, винта с правой резьбой. Это простая договоренность. Получается, что результатом векторного произведения является не совсем «честный» вектор. Такие вектора называются аксиальными, или псевдовекторами, в отличие от обычных полярных векторов. Аксиальные вектора хорошо передают свойства вращения.

Приводим без доказательства сводку правил векторной алгебры:

A×B=Скаляр=A_xB_x+A_yB_y+A_zB_z,

A´B=Вектор,

(A´B)_z=A_xB_y-A_yB_x,

(A´B)_x=A_yB_z-A_zB_y,

(A´B)_y=A_zB_x-A_xB_z,

A´A=0,

A×(A´B)=0,

A×(B´C)=(A´B)×C,

A´(B´C)=B(A×C)-C(A×B)

Сведения из дифференциального исчисления:

Приращение функции y(x,y,z) через малые приращения аргументов (Dх, Dу, Dz) можно вычислить по формуле:

Точность этой формулы возрастает при уменьшении приращений аргументов.

Порядок дифференцирования функции нескольких переменных не влияет на результат:

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

Производные полей - градиент

Когда поля меняются со временем, то их изменение можно описать, задав их производные по t. Мы хотим также описать и их изменение в пространстве, потому что мы интересуемся связью, скажем, между температурой в некоторой точке и в точке с ней рядом. Как же задать производную температуры по координате? Дифференцировать температуру по х? Или по у, или по z?

Осмысленные физические законы не зависят от ориентации системы координат. Поэтому их нужно писать так, чтобы по обе стороны знака равенства стояли скаляры или векторы. Что же такое производная скалярного поля, скажем, ? Скаляр ли это, или вектор, или еще что? Это ни то и ни другое, потому что если взять другую ось х, то изменится. Но у нас есть три возможные производные: , , . Три сорта производных, а ведь мы знаем, что нужно как раз три числа, чтобы образовать вектор. Может быть, что три производные и представляют собой компоненты вектора:

Вектор ли это?

Вообще говоря, не из любых трех чисел можно составить вектор. О векторе можно говорить только тогда, когда при повороте системы координат компоненты преобразуются по правильному закону (такому же, как и тройка чисел х, у, z). Так что следует проследить, как меняются эти производные при повороте системы координат. Мы покажем, что действительно вектор. Производные действительно преобразуются при вращении системы координат так, как полагается.

В этом можно убедиться по-разному. Можно, например, задать себе вопрос, ответ на который не должен зависеть от системы координат, и попытаться выразить ответ в «инвариантной» форме. К примеру, если S = A×B и если А и В - векторы, то мы знаем, что S - скаляр (число не зависящее от выбора системы координат). Мы знаем, что S - скаляр, не проверяя, меняется ли он при изменении системы координат. Ему ничего иного не остается, раз он является скалярным произведением двух векторов. Подобным же образом, если мы знаем, что А - вектор, и у нас есть три числа В₁, В₂, В₃, и мы обнаруживаем, что

А_хВ₁ + А_уВ₂ + А_zB₃ = S

где S в любой системе координат одно и то же), то три числа В₁, В₂, В₃ обязаны быть компонентами В_х, В_у, В_z некоторого вектора В.

Рассмотрим теперь температурное поле. Возьмем две точки Р₁ и Р₂, разделенные маленьким расстоянием . Температура в Р₁ есть Т₁, а в Р₂ она равна Т₂, и их разница DТ = Т₂ - Т₁. Температура в этих реальных физических точках, конечно, не зависит от того, какие оси мы выбрали для измерения координат. В частности, DТ - тоже число, не зависящее от системы координат. Это скаляр.

Выбрав удобную систему координат, мы можем записать

Т₁ = Т(х, у, z) и Т₂ = Т(х + Dх, у + Dу, z + Dz),

где Dх, Dу, Dz - компоненты вектора (рисунок). Вспомнив формулу из дифференциального исчисления

, напишем

Слева стоит скаляр, а справа - сумма трех произведений каких-то чисел на Dх, Dу, Dz, которые являются компонентами вектора. Значит, три числа

тоже х-, у-, z-компоненты вектора. Мы напишем этот новый вектор при помощи символа . Символ (называемый набла) напоминает нам о дифференцировании. Читают по-разному: «набла Т», или «градиент Т», или «grad T»:

C этим обозначением формула

переписывается в более компактной форме

DT = ÑТ×DR

Или, выражая словами: разница температур в двух близких точках есть скалярное произведение градиента ÑТ на вектор DR смещения второй точки относительно первой. Последнее уравнение также служит иллюстрацией к нашему утверждению, что ÑТ - действительно вектор.

Оператор Ñ

Доказательство того, что ÑТ является вектором, не зависит от того, какое скалярное поле мы дифференцируем. Все доводы остались бы в силе, если бы Т было заменено любым скалярным полем. А поскольку уравнения преобразований компонент вектора ÑТ при повороте системы координат (см. раздел Векторы) одинаковы независимо от того, что дифференцируется, то можно Т убрать и уравнение преобразования, например, х-компоненты вектора ÑТ заменить операторным уравнением:

Мы оставляем операторы «жаждущими продифференцировать что угодно».

Так как сами дифференциальные операторы преобразуются как компоненты векторного поля, то можно назвать их компонентами векторного оператора. Можно написать

или

Мы абстрагировали градиент от Т. Это одна из замечательных идей, которые украшают математику.

Необходимо все время помнить, что Ñ - это оператор. Сам по себе он ничего не означает. Вектор можно умножить на скаляр, например, на температуру Т, а произведение ÑТ - это уже не «жаждущий» оператор, его жажда утолена. Это физическая величина, имеющая смысл. Она представляет собой скорость пространственного изменения Т: х-компонента ÑТ показывает, насколько быстро Т изменяется в х-направлении. А куда направлен вектор ÑТ? Мы знаем, что скорость изменения Т в каком-то направлении - это компонента ÑТ в этом направлении (вспомним выражение DT = ÑТ×DR). Отсюда следует, что направление ÑТ обладает самой длинной проекцией; иными словами, то направление, по которому Т меняется быстрее всего. Направление градиента Т - это направление быстрейшего подъема величины Т.

Операции с Ñ

Можно ли с векторным оператором Ñ производить другие алгебраические действия? Попробуем скомбинировать его с вектором. Из двух векторов можно составить скалярное произведение, например

Ñ×Е = Ñ_хЕ_х + Ñ_уЕ_у + Ñ_zE_z =

Полученная сумма инвариантна относительно преобразования координат. Если повернуть оси координат, то каждое из трех чисел, входящих в сумму изменится, однако так, что сумма останется неизменной. Итак, Ñ×Е- это скалярное поле, и оно должно представить собой некоторую физическую величину.

Скалярная величина Ñ×(Вектор) очень широко применяется в физике. Ей присвоили имя «дивергенция», или «расходимость». Например,

Ñ×Е =div E = «Дивергенция Е»

Можно было бы, как и для ÑТ, описать физический смысл Ñ×Е. Но мы сделаем это далее, в разделе «Интегральное исчисление векторов».

Посмотрим сначала, что можно еще извлечь из векторного оператора Ñ. Как насчет векторного произведения? Можно надеяться, что

Ñ´Е = Вектор

Компоненты этого вектора можно написать, пользуясь, пользуясь обычным правилом для векторного произведения:

(Ñ´Е)_х = Ñ_уЕ_z - Ñ_zЕ_y =

(Ñ´Е)_y = Ñ_zЕ_x - Ñ_xЕ_z =

(Ñ´Е)_z = Ñ_xЕ_y - Ñ_yЕ_x =

Комбинацию Ñ´Еназывают «ротор» (пишут rot E), или (редко) «вихрь». Происхождение этого названия и физический смысл комбинации мы обсудим ниже.

В итоге мы получили три сорта комбинаций, куда входит Ñ:

ÑТ = grad T = Вектор,

Ñ×E = div E = Скаляр,

Ñ´E = rot E = Вектор.

Используя эти комбинации, пространственные вариации полей можно записывать в удобном виде, т.е. в виде, не зависящем от той или иной совокупности осей координат.

В качестве примера применения векторного дифференциального оператора Ñ выпишем совокупность векторных уравнений, в которой содержатся законы электромагнетизма. Их называют уравнениями Максвелла.

Уравнения Максвелла

где r - «плотность электрического заряда» (количество заряда в единице объема), а j - «плотность электрического тока» (скорость протекания заряда сквозь единицу площади). Эти четыре уравнения содержат в себе законченную классическую теорию электромагнитного поля. Обратите внимание на простоту и элегантность записи, которая стала возможной за счет использования векторного оператора Ñ.

Вторые производные векторных полей

Из вторых производных можно составить несколько комбинаций:

(а) Ñ×(ÑТ) = Ñ²Т = =Скалярное поле (скалярный оператор Ñ² называется оператором Лапласа, или лапласианом),

Ñ(Ñ×Е)= Ñ²Е =Векторное поле (лапласиан действует на каждую проекцию вектора Е).

(б) Ñ´(ÑТ) = 0 (векторное произведение взаимно параллельных векторов),

(в) Ñ(Ñ×Е) =Векторное поле,

(г) Ñ×(Ñ´Е) =0 (скалярное произведение взаимно перпендикулярных векторов),

(д) Ñ´(Ñ´Е) =Ñ(Ñ×Е) - Ñ²Е.

Можно убедиться, что никаких иных комбинаций быть не может.

Посмотрим сперва на вторую комбинацию (б). Она имеет ту же форму, что и

А´(АТ) = (А ´ А) Т = 0,

потому что А ´ А всегда нуль. Значит,

rot(grad N) = Ñ´(ÑТ) = 0.

Можно понять, как это получается, если расписать одну из компонент:

что равно нулю (вспомним уравнение из дифференциального исчисления). Это же верно и для других компонент. Стало быть, Ñ´(ÑТ) = 0 для любого распределения температур, да и для всякой скалярной функции.

Возьмем второй пример. Посмотрим, нельзя ли получить нуль другим путем. Скалярное произведение вектора на векторное произведение, содержащее этот вектор, равно нулю

А×(А´В) =0,

потому что А´Вперпендикулярно к А и не имеет тем самым составляющих вдоль А. Сходная комбинация стоит под обозначением (г):

Ñ×(Ñ´Е) =div (rotE) = 0.

В справедливости этого равенства легко убедиться, проделав выкладки на компонентах.

Сформулируем без доказательства две теоремы, которые весьма полезны в физике, в частности в теории электромагнетизма.

В физических задачах часто оказывается, что ротор какой-то величины (скажем векторного поля А) равен нулю. Мы видели, что ротор градиента всегда равен нулю. Далее, может оказаться, что А будет градиентом какой-то величины, потому что тогда ротор А с необходимостью обратится в нуль. Имеется теорема, утверждающая, что если ротор А есть нуль, то тогда А непременно окажется чьим-то градиентом; существует некоторое скалярное поле y (пси), такое, что А = grad y. иными словами, справедлива

Теорема:

Если Ñ´А= 0, то имеется y, такое, что А= Ñy.

Сходная теорема формулируется и для случая, когда дивергенция А есть нуль. Мы видели (г), что дивергенция ротора любой величины равна всегда нулю. Если нам встретилось векторное поле D, для которого div D - нуль, то мы вправе заключить, что D - это ротор некоторого векторного поля С.

Теорема:

Если Ñ×D= 0, то имеется С, такое, что D= Ñ´C.

Займемся теперь комбинациями, которые не равны нулю. Возьмем комбинацию (а) Ñ×(ÑТ). В общем случае это не нуль.

Выпишем компоненты

Далее,

что может, вообще говоря, быть любым числом. Это скалярное поле.

Скобок можно не ставить, а вместо этого писать:

Можно рассматривать Ñ² как новый оператор. Это скалярный оператор. Так как он в физике встречается часто, ему дали особое имя - лапласиан.

Лапласиан = .

Раз оператор лапласиана - оператор скалярный, он может действовать и на вектор. Под этим мы подразумеваем, что он применяется к каждой компоненте вектора

Ñ²А = (Ñ²А_х, Ñ²А_у, Ñ²А_z).

Последняя комбинация (д) дает векторное поле, которое может случайно возникнуть в каком-нибудь расчете. Ее можно вывести, расписывая компоненты.

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ВЕКТОРОВ

Векторные интегралы; криволинейный интеграл от Ñy

В предыдущей главе мы видели, что брать производные от поля можно по разному. Одни приводят к векторным полям, другие - к скалярным. Хотя формул было приведено довольно много, все их можно подытожить одним правилом: операторы суть три компоненты векторного оператора Ñ.

Мы уже говорили о смысле операции градиента (Ñ на скаляр). Обратимся теперь к смыслу операций вычисления дивергенции и ротора. Толкование этих величин лучше всего сделать на языке векторных интегралов и уравнений, связывающих эти интегралы. Одна из этих интегральных формул практически тривиальна, а две другие - нет. Эти формулы фактически являются математическими теоремами. Они полезны не только для толкования смысла и содержания понятий дивергенции и ротора, но и при разработке общих физических теорий. Для теории полей эти математические теоремы - все равно, что теорема о сохранении энергии для механики частиц. Подобные теоремы общего характера очень важны для более глубокого понимания физики. Кроме того, многие практические задачи мы решим, воспользовавшись этими тремя интегральными формулами.

Начнем с той интегральной формулы, куда входит градиент. Мысль, которая содержится в ней, очень проста: раз градиент есть быстрота изменения величины поля, то интеграл от этой быстроты даст нам общее изменение поля. Пусть у нас есть скалярное поле y(х, у, z). В двух произвольных точках (1) и (2) функция y имеет соответственно значения y(1) и y(2). [Используется такое удобное обозначение: (2) означает точку (х₂, у₂, z₂), а y(2) - это то же самое, что y(х₂, у₂, z₂).] Если Г (гамма) - произвольная кривая, соединяющая (1) и (2) (рисунок), то справедлива

Теорема

Интеграл, стоящий здесь, - это криволинейный интеграл от (1) до (2) вдоль кривой Г от скалярного произведения вектора Ñy на другой вектор, ds, являющийся бесконечно малым элементом дуги кривой Г [направленной от (1) к (2)].

Разность значений скалярного поля в двух точках равна криволинейному интегралу от касательной составляющей градиента этого скаляра вдоль любой кривой, соединяющей первую точку со второй.

Поток векторного поля

Прежде чем рассматривать следующую интегральную теорему - теорему о дивергенции, - необходимо разобраться в одной идее, смысл которой в случае, например, потока тепла легко усваивается. Определим вектор h плотности потока тепла (вместо слова «тепла» можно подставить - заряда, жидкости, энергии электромагнитного поля и т.д. - чего угодно) как количество тепла, протекающего сквозь единицу площади, перпендикулярной направлению потока тепла, в единицу времени. Направление вектора h совпадает с направлением потока тепла в данной точке пространства. Положим, что внутри тела имеется замкнутая поверхность S, ограничивающая объем V (рисунок). Нам хочется узнать, сколько тепла вытекает из этого объема. Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S.

Обозначим через da площадь элемента поверхности. Этот символ заменяет двумерный дифференциал. Если, например, элемент окажется в плоскости ху, то

da = dx dy.

Позже мы будем иметь дело с интегралами по объему, и тогда будет удобно рассматривать элемент объема в виде малого кубика и обозначать его dV, подразумевая, что

dV = dx dy dz.

Поток тепла через элемент поверхности da равен произведению площади на составляющую h, перпендикулярную к da. Введем единичный вектор n, определяющий направление нормали к элементу поверхности da (рисунок). Искомая составляющая h равна

h_n = h×n,

и тогда поток тепла сквозь da равен

h×nda.

А весь поток тепла через произвольную поверхность получается суммированием вкладов от всех элементов поверхности. Иными словами предыдущее выражение интегрируется по всей поверхности

Поток тепла сквозь S (из объема V) .

Этот интеграл мы будем называть «поток h через поверхность». Мы рассматриваем h как «плотность потока» тепла, а поверхностный интеграл от h - это общий поток тепла наружу через поверхность, т.е. тепловая энергия за единицу времени (джоули в секунду).

Мы хотим эту идею обобщить на случай, когда вектор не представляет собой потока какой-то величины, а, скажем, является электрическим полем. Конечно, если это будет нужно, то и в этом случае все равно можно проинтегрировать нормальную составляющую электрического поля по площади. Хотя теперь она уже не будет ничьим потоком, мы все еще будем употреблять слово «поток». Мы будем говорить, что

Поток Е сквозь поверхность S .

Слову «поток» мы придаем смысл «поверхностного интеграла от нормальной составляющей» некоторого вектора. То же определение будет применяться и тогда, когда поверхность незамкнута.

А возвращаясь к частному случаю потока тепла, обратим внимание на те случаи, когда количество тепла сохраняется. Представим себе, к примеру, материал, в котором после первоначального подогрева не происходит ни дальнейшего подвода, ни поглощения тепла. Тогда, если из какой-то замкнутой поверхности наружу поступает тепло, содержание тепла во внутреннем объеме должно падать. Так что в условиях, когда количество тепла сохраняется, мы говорим, что

, где Q - запас тепла внутри S.

Это толкование возможно оттого, что речь идет о потоке тепла, и оттого, что мы предположили, что количество тепла сохраняется. Конечно, если бы внутри объема создавалось тепло, нельзя было бы говорить о полном запасе тепла в нем.

Укажем теперь на интересное свойство потока любого вектора. Можем при этом представлять себе вектор потока тепла, но верно это будет и для произвольного векторного поля С. Представим себе замкнутую поверхность S, окружающую объем V. Разобьем теперь объем на две части каким-то «сечением» (рисунок). Объем V₁ окружен поверхностью S₁, составленной частью из прежней поверхности S_а и частью из «сечения» S_а_b. Объем V₂ окружен поверхностью S₂, составленной частью из прежней поверхности S_b и замкнутой сечением S_а_b. Поток через поверхность S равен сумме потоков через поверхность S₁ и S₂. Действительно:

Поток сквозь S₁ =

Поток сквозь S₂ =

Заметим, что во втором интеграле мы обозначили внешнюю нормаль к S_а_b буквой n₁, если она относится к S₁, и буквой n₂, если она относится к S₂ (рисунок). Ясно, что n₁ = - n₂, и тем самым

Складывая теперь уравнения для потоков сквозь S₁ и S₂, мы убеждаемся, что сумма потоков как раз равна сумме двух интегралов, которые, взятые вместе, дают поток через первоначальную поверхность S = S_a + S_b.

Мы видим, что поток через всю внешнюю поверхность S можно рассматривать как сумму потоков из тех двух частей, на которые разрезан объем. Эти части можно еще разрезать: скажем, V₁ разбить пополам. Опять придется прибегнуть к тем же доводам. Так что для любого способа разбиения первоначального объема всегда остается справедливым то свойство, что поток через внешнюю поверхность (первоначальный интеграл) равен сумме потоков изо всех внутренних частей.

Теорема Остроградского-Гаусса

Приведем без доказательства теорему, доказывающую, что дивергенция произвольного вектора в какой-то точке пространства равна потоку этого вектора, приходящемуся на единицу объема (объемной плотности потока в данной точке пространства). Таким образом, дифференциальная характеристика векторного поля - дивергенция, связана с интегральной характеристикой - способностью векторного поля формировать поток.

Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности S (поток вектора через замкнутую поверхность S) равен интегралу от дивергенции вектора по объему V, лежащему внутри этой поверхности:

Объемный интеграл суммирует потоки из всех бесконечно малых частей объема V (вспомним, что поток из объема равен сумме потоков из всех частей этого объема) и дает, тем самым, общий поток через поверхность S, ограничивающую объем V.

Циркуляция векторного поля

Рассмотрим ротор поля примерно так же, как рассматривали дивергенцию. Связь дивергенции с интегралом по поверхности (потоком векторного поля), которая следует из теоремы Остроградского Гаусса заранее вовсе не очевидна. Эта связь является предметом доказательствав данной теореме. Столь же неочевидной является связь ротора с другой характеристикой поля - циркуляцией. Рассмотрим теорему Стокса, которая описывает эту связь. Вначале рассмотрим понятие циркуляции векторного поля.

Если С - произвольное векторное поле, мы возьмем его составляющую вдоль кривой линии и проинтегрируем эту составляющую по замкнутому контуру. Интеграл называется циркуляцией векторного поля по контуру.

Пусть Г - произвольный замкнутый контур в пространстве (воображаемый, разумеется). Пример мы видим на рисунке. Криволинейный интеграл от касательной составляющей С по контуру записывается в виде

Заметим, что интеграл берется по всему замкнутому пути, а не от одной точки до другой. Кружочек на знаке интеграла должен нам напоминать об этом. Такой интеграл называется циркуляцией векторного поля по кривой Г. Название связано с тем, что первоначально так рассчитывали циркуляцию жидкости. Но название это, как и поток, было распространено на любые поля, даже такие, в которых «циркулировать» нечему.

По аналогии с потоком можно доказать, что циркуляция вдоль контура есть сумма циркуляций вдоль двух меньших контуров. Положим, что, соединив две точки (1) и (2) первоначальной кривой с помощью некоторой линии, мы разбили кривую на два контура Г₁ и Г₂ (рисунок).

Контур Г₁ состоит из Г_а - части первоначальной кривой слева от (1) и (2) и «границы» Г_ab. Контур Г₂ состоит из остатка первоначальной кривой плюс та же граница.

Циркуляция вдоль Г₁ есть сумма интеграла вдоль Г_а и вдоль Г_ab. Точно так же и циркуляция вдоль Г₂ есть сумма двух частей, одной вдоль Г_b, другой - вдоль Г_ab. Интеграл вдоль Г_ab для кривой Г₂ имеет знак, противоположный тому знаку, который он имел для кривой Г₁, потому что направление обхода противоположны (в обоих криволинейных интегралах направления поворота нужно брать одни и те же).

Повторяя прежние аргументы, мы можем убедиться, что сумма двух циркуляций даст как раз криволинейный интеграл вдоль кривой Г. Интегралы по Г_ab сократятся. Циркуляция по одной части плюс циркуляция вдоль другой равняется циркуляции вдоль внешней линии. Этот процесс разрезания большого контура на меньшие можно продолжить. При сложении циркуляций по меньшим контурам смежные части будут сокращаться, так что сумма сведется к циркуляции вдоль единственного первоначального контура.

Теперь предположим, что первоначальный контур - это граница некоторой поверхности. Существует бесконечное множество поверхностей, границей которых служит все тот же первоначальный замкнутый контур. Наши результаты не зависят, однако, от выбора этих поверхностей. Сперва мы разобьем наш первоначальный контур на множество малых контуров, лежащих на выбранной поверхности (рисунок). Какой бы ни была форма поверхности, циркуляция по Г есть сумма циркуляций по всем маленьким контурам.

Теорема Стокса:

Криволинейный интеграл от касательной составляющей произвольного вектора по замкнутому контуру Г (циркуляция вектора по замкнутому контуру Г) равен поверхностному интегралу от нормальной составляющей ротора этого вектора по произвольной поверхности S, ограниченной этим контуром:

Теорему следует дополнить соглашением о знаках. Как вообще узнавать, какое направление надо выбирать для положительного направления «нормальной» компоненты вектора Ñ´С? «Положительную» нормаль надо связывать с направлением обхода вдоль контура пользуясь правилом правого винта. При таком условии знаки левой и правой части выражения в теореме Стокса совпадают.

Получается, что нормальная к элементу поверхности компонента ротора произвольного вектора равна поверхностной плотности циркуляции этого вектора в точках данного элемента поверхности. Такова связь ротора с циркуляцией векторного поля.

Таким образом:

дивергенцияхарактеризует способность векторного поля формировать поток. Она равна объемной плотности потока векторного поля. Поток вектора из какой-то заданной области пространства есть сумма потоков из бесконечно малых объемов, на которые можно разделить эту область пространства, то есть интеграл по объему от дивергенции вектора.

ротор -вектор,характеризующий способность векторного поля формировать циркуляцию. Проекция ротора на направление нормали к поверхности равна поверхностной плотности циркуляции векторного поля. Циркуляция вектора вдоль какого-то замкнутого контура равна сумме циркуляций вдоль бесконечно малых участочков произвольной поверхности, которую ограничивает контур, то есть интегралу по этой поверхности от нормальной составляющей ротора.

Итоги

Подытожим самые существенные моменты из математики векторных полей.

1. Операторы

, ,

можно рассматривать как три составляющие векторного оператора Ñ; формулы, следующие из векторной алгебры, остаются правильными, если этот оператор считать вектором

2. Разность значений скалярного поля в двух точках равна криволинейному интегралу от касательной составляющей градиента этого скаляра вдоль любой кривой, соединяющей первую точку со второй:

3. Поверхностный интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности равен интегралу от дивергенции вектора по объему, лежащему внутри этой поверхности:

4. Криволинейный интеграл от касательной составляющей произвольного вектора по замкнутому контуру равен поверхностному интегралу от нормальной составляющей ротора этого вектора по произвольной поверхности, ограниченной этим контуром