 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Аперіодична ланка другого порядку
Коливальна ланка Коливальною називається ланка, яка описується рівнянням другого порядку
де Операційне рівняння:
Передавальна функція ланки:
Частотні функції мають вигляд:
При
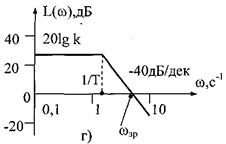
тобто при Асимптотична ЛАЧХ побудована аналогічно ЛАЧХ аперіодичної ланки:
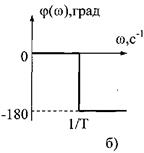
У частоті сполучення Частотні характеристики наведені на рис. 8.
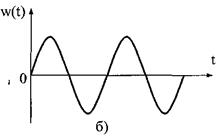
Рис.8. Частотні характеристики коливальної ланки: АЧХ (а); ФЧХ (б); АФЧХ (в); ЛАЧХ (г); ЛФЧХ (д) Розв'язуючи рівняння (1) ланки при x(t)=l(t) та за нульових початкових умов (у(0)=0; у'(0)=0), отримаємо перехідну функцію ланки:
де Перехідна характеристика має вигляд затухаючих коливань, усталене значення яких дорівнює коефіцієнту k (рис.9, а). Імпульсна перехідна функція ланки(рис.9, б):
Рис. 9. Перехідна (а) та імпульсна перехідна (б) характеристики коливальної ланки До коливальних ланок належать елементи САК, що містять два накопичувача енергії, в одному з яких накопичується потенціальна енергія, а в іншому - кінетична. Окрім того, має бути елемент, що розсіює цю енергію, тобто канал, по якому накопичувачі обмінюються енергією. Мірою витрати енергії в каналі обміну і є коефіцієнт затухання Консервативна ланка Якщо опір каналу обміну енергії дорівнює нулю, тобто
Цьому рівнянню відповідає передавальна функція
Частотні функції ланки:
Із цих виразів видно, що АЧХ на частоті
Рис.10. Частотні характеристики консервативної ланки: АЧХ (а); ФЧХ (б); АФЧХ (в) Перехідна функція ланки:
Перехідна характеристика (рис.11,а) має вигляд незатухаючих гармонічних коливань навколо значення k . Імпульсна перехідна функція:
Відповідна характеристика також має вигляд незатухаючих гармонічних коливань, але навколо нуля (рис. 11, б).
Рис. 11. Перехідна (а) та імпульсна перехідна (б) характеристики консервативної ланки Аперіодична ланка другого порядку Якщо коефіцієнт затухання
де Цю ланку можна уявити як послідовне з'єднання двох аперіодичних ланок першого порядку, тому вона не належить до числа елементарних ланок. Відмітимо, що аперіодичною ланкою другого порядку може бути описаний ДПС НЗ середньої потужності, для якого Форсуюча ланка Форсуючою називається ланка, яка описується рівнянням
Операційне рівняння і передавальна функція:
Частотні функції:
Рис.12. Частотні характеристики форсуючої ланки: АЧХ (а); ФЧХ (б); АФЧХ (в); ЛАЧХ (г)
при при АФЧХ являє собою пряму, що паралельна уявній вісі та перетинає дійсну вісь у точці U = k. Частотні характеристики наведені на рис. 12. Часові функції форсуючої ланки:
|



 (1)
(1) (ксі) – коефіцієнт затухання або демпфування
(ксі) – коефіцієнт затухання або демпфування  .
.


 амплітуда
амплітуда  , тобто для різних значень коефіцієнта затухання
, тобто для різних значень коефіцієнта затухання  на частоті
на частоті  , яку називають резонансною, амплітуда набуває значень від k/2 до
, яку називають резонансною, амплітуда набуває значень від k/2 до  (рис. 8, а:
(рис. 8, а:  ).
).
 ,
, 
 , при
, при 
 , при
, при  - пряма з нахилом –40 дБ/дек.
- пряма з нахилом –40 дБ/дек. при малих значеннях коефіцієнта затухання асимптотична ЛАЧХ дуже відрізняється від точної ЛАЧХ.
при малих значеннях коефіцієнта затухання асимптотична ЛАЧХ дуже відрізняється від точної ЛАЧХ.




 ;
; 



 зі збільшенням витрат збільшується
зі збільшенням витрат збільшується  ; зі зменшенням
; зі зменшенням  (не втрачається енергія), то коливальна ланка вироджується в консервативну (резонансну) ланку, рівняння якої має вигляд:
(не втрачається енергія), то коливальна ланка вироджується в консервативну (резонансну) ланку, рівняння якої має вигляд: (2)
(2)
 ;
;  ;
;  ;
;  ;
;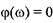 , при
, при  ;
;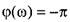 , при
, при 
 має розрив, а ФЧХ - східчасто змінює своє значення з 0 на
має розрив, а ФЧХ - східчасто змінює своє значення з 0 на  (рис. 10).
(рис. 10).




 , то передавальну функцію коливальної ланки можна привести до вигляду:
, то передавальну функцію коливальної ланки можна привести до вигляду: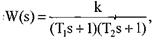 (3)
(3)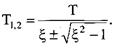

 (4)
(4)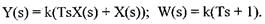




 при
при 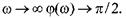






 - пряма з нахилом +20 дБ/дек.
- пряма з нахилом +20 дБ/дек.
