Линейно-зависимая и линейно-независимая система векторов. Базис. Разложение вектора по базису.
Линейные операции над векторами Геометрические задачи 1. Задайте произвольно векторы  на плоскости и постройте: на плоскости и постройте: а)  ; б) ; б)  ; в) ; в)  ; г) ; г) 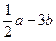 ; д) ; д)  ; е) ; е)  . . 2. Сторона  треугольника треугольника  разделена точками разделена точками  и и  на три равные части. Обозначив на три равные части. Обозначив  и и  , выразите через , выразите через  и и  векторы векторы  и и  . . 3. В параллелограмме  имеем имеем  и и  . Выразите через . Выразите через  и и  следующие векторы: следующие векторы:    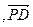 где где  — точка пересечения диагоналей параллелограмма. — точка пересечения диагоналей параллелограмма. 4. На стороне  треугольника треугольника  взята точка взята точка  так, что прямая так, что прямая  -биссектриса угла при вершине -биссектриса угла при вершине  . Выразите через . Выразите через  и и  следующие векторы: следующие векторы:  5. В параллелограмме  вершина вершина 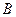 соединена с серединой соединена с серединой  стороны стороны  . Найдите, в каком отношении отрезок . Найдите, в каком отношении отрезок  делит диагональ делит диагональ  . . 6. В правильном пятиугольнике  заданы векторы, совпадающие с его сторонами заданы векторы, совпадающие с его сторонами  , ,  , ,  , ,  , ,  . Построить векторы 1) . Построить векторы 1) 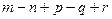 ; 2) ; 2)  ; 3) ; 3)  . . 7. В параллелепипеде  заданы векторы, совпадающие с его ребрами заданы векторы, совпадающие с его ребрами  , ,  и и  . Построить следующие векторы: 1) . Построить следующие векторы: 1)  ; 2) ; 2) 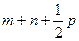 ; 3) ; 3)  . . 8. Доказать, что если медианы треугольника ABCпересекаются в точке М, то: а)  ; б) ; б)  9. Пусть биссектриса угла А треугольника ABC пересекает противоположную сторону в точке L.Выразить вектор, однонаправленный с вектором  , через векторы , через векторы  и и 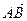 . . Аналитические задачи 1. Векторы  и и  , имеющие равные длины, отложены от общего начала. Докажите, что вектор , имеющие равные длины, отложены от общего начала. Докажите, что вектор  , если отложить его от того же начала, будет направлен по биссектрисе угла между , если отложить его от того же начала, будет направлен по биссектрисе угла между  и и  . . 2. Точка  является центром масс треугольника является центром масс треугольника  . Доказать, что . Доказать, что  3. Векторы  и и  отложены от общего начала. Докажите, что вектор отложены от общего начала. Докажите, что вектор  если отложить его от того же начала, будет направлен по биссектрисе угла между если отложить его от того же начала, будет направлен по биссектрисе угла между  и и  . . 4. Докажите, что для любых векторов  и и  справедливо неравенство справедливо неравенство  . В каком случае левая часть равна правой? . В каком случае левая часть равна правой? 5. Какому условию должны удовлетворять векторы  и и  чтобы: чтобы: 6. а)  ; б) ; б)  ; в) ; в) 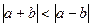 ? ? 7. На плоскости даны треугольник  и точка и точка  . Построена точка . Построена точка  такая, что такая, что  Докажите, что сумма векторов Докажите, что сумма векторов  равна нулю. Как обобщить эту задачу на случай равна нулю. Как обобщить эту задачу на случай  - угольника? - угольника? 8. Докажите, что не может быть двух разных точек  и и  таких, что таких, что  и и  9. Докажите, что отрезки, соединяющий середины противоположных ребер тетраэдра, пересекаются, причем точка пересечения делит каждый из этих Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основанию. 10. Доказать, что  — параллелограмм, если — параллелограмм, если  , ,  , ,  . . Алгебраические задачи: 1. При каких значениях  и и  коллинеарны векторы: коллинеарны векторы: а)  , ,  ; б) ; б) 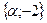 , ,  . . 2. На плоскости даны четыре точки  Проверьте, что четырехугольник Проверьте, что четырехугольник  -параллелограмм. -параллелограмм. 3. Даны три точки:  . Найдите четвертую точку . Найдите четвертую точку  так, чтобы четырехугольник так, чтобы четырехугольник  был параллелограммом. был параллелограммом. 4. Покажите, что четыре точки  являются вершинами трапеции. являются вершинами трапеции. 5. Даны  , ,  и и  . Вычислить . Вычислить  . . 6. Векторы  и и  взаимно перпендикулярны, причем взаимно перпендикулярны, причем  и и  . Определить . Определить  и и  . . 7. Векторы  и и  образуют угол образуют угол  , причем , причем  и и  . Определить . Определить  и и  . . 8. Три силы  , , 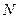 и и  , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей  , если известно, что , если известно, что  , ,  и и 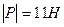 . . 9. Два вектора  и и  приложены к одной точке. Определить координаты вектора приложены к одной точке. Определить координаты вектора  , направленного по биссектрисе угла между векторами , направленного по биссектрисе угла между векторами  и и  , при условии, что , при условии, что  . . 10. Может ли некоторый ненулевой вектор образовывать с векторами  , ,  и и  углы, равные соответственно: а) 120°, 135°, 45°; б) 120°, 135°, 60°. углы, равные соответственно: а) 120°, 135°, 45°; б) 120°, 135°, 60°. 11. Найти значения параметра при которых вектор  имеет длину, равную 5, и образует с вектором имеет длину, равную 5, и образует с вектором  тупой угол. тупой угол.
12. Найти значения параметра 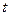 при которых вектор при которых вектор  a) образует с вектором a) образует с вектором  угол 90°; б) коллинеарен вектору угол 90°; б) коллинеарен вектору  ; в) является противоположно направленным вектору ; в) является противоположно направленным вектору  . . Линейно-зависимая и линейно-независимая система векторов. Базис. Разложение вектора по базису. Геометрические задачи 1. Дана пирамида с вершинами  , , 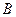 , ,  , ,  . Точки . Точки  и и  - середины ребер - середины ребер  и и  соответственно. Найти координаты вектора соответственно. Найти координаты вектора  в базисе в базисе  , ,  , ,  . [1, с. 19] . [1, с. 19] 2. В правильном шестиугольнике  имеем имеем  и и 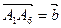 . Разложите по базису . Разложите по базису  , ,  векторы векторы  , ,  , ,  . [1, с. 27] . [1, с. 27] 3. Три силы  , ,  , ,  , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину равнодействующей , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину равнодействующей  , если известны величины сил , если известны величины сил 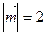 , , 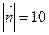 , ,  . [2, с. 81] . [2, с. 81] 4. Разложить вектор скорости ветра (10  ), направленного с северо-запада под углом ), направленного с северо-запада под углом 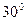 к северу, на компоненты, имеющие направления на север и запад. [2, с. 81] к северу, на компоненты, имеющие направления на север и запад. [2, с. 81] 5. В ромбе  даны диагонали даны диагонали  и и  . Разложить по этим двум векторам все векторы, совпадающими со сторонами ромба: . Разложить по этим двум векторам все векторы, совпадающими со сторонами ромба:  , ,  , ,  , ,  . [2, с. 82] . [2, с. 82] 6. В тетраэдре  даны ребра, выходящие из вершины даны ребра, выходящие из вершины  : :  , ,  , ,  . Выразить через эти векторы остальные ребра тетраэдра, медиану . Выразить через эти векторы остальные ребра тетраэдра, медиану  , грани , грани  и вектор и вектор 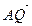 , где , где  – центр тяжести грани – центр тяжести грани  . [2, с. 82] . [2, с. 82] 7. Выяснить могут ли векторы 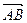 , ,  , ,  образовывать базис в пространстве образовывать базис в пространстве  ? ? 8. Пусть биссектриса угла  треугольника треугольника  пересекает противоположную сторону в точке пересекает противоположную сторону в точке  . Найти координаты вектора . Найти координаты вектора 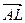 в базисе в базисе 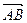 , ,  . . 9. Доказать, что равновесие точки невозможно под действием двух неколлинеарных сил. [4, с. 43] 10. Доказать, что равновесие точки невозможно под действием трех некомпланарных сил. [4, с. 43] 11. Докажите, что любые четыре геометрических вектора линейно зависимы. [5, с. 36] 12. В правильном шестиугольнике  точка точка  - центр описанной окружности. Могут ли вектора - центр описанной окружности. Могут ли вектора  , ,  образовывать базис в образовывать базис в  ? Ответ обосновать. ? Ответ обосновать. 13. Проверить линейную зависимость диагоналей граней куба   , , 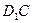 , ,  . . 14. Точки  и и  принадлежат соответственно прямым принадлежат соответственно прямым  и и  , которые пересекаются в некоторой точке , которые пересекаются в некоторой точке  . Выразить через . Выразить через  и и  векторы, направленные по биссектрисам углов между прямыми. [1, с. 76] векторы, направленные по биссектрисам углов между прямыми. [1, с. 76] 15. При выполнении какого условия равнодействующая двух сил, приложенных к одной точке, будет направлена по биссектрисе угла между ними? Ответ обосновать. [1, с. 76] 16. Дан четырехугольник  . Точки . Точки  и и  - середины сторон - середины сторон  и и  . Выразить вектор . Выразить вектор 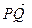 через векторы через векторы 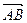 , ,  , , 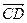 . [1, с. 10] . [1, с. 10] 17. дан параллелограмм  . Точки . Точки  и и  - середины сторон - середины сторон  и и  соответственно. Найти координаты вектора соответственно. Найти координаты вектора 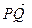 , если за базисные векторы приняты , если за базисные векторы приняты  и и  . [1, с. 15] . [1, с. 15] 18. Проверить линейную зависимость диагоналей граней куба   , , 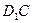 , ,  . . 19. В правильном шестиугольнике  имеем имеем  и и  . Разложить по базису . Разложить по базису  векторы векторы  Алгебраические задачи 1. Проверить, что векторы  и и  на плоскости не коллинеарны, и разложить вектор на плоскости не коллинеарны, и разложить вектор  по базису по базису  , ,  . [1, с. 20] . [1, с. 20] 2. Пусть векторы  и и  образуют базис в образуют базис в  . Могут ли векторы . Могут ли векторы  , ,  образовывать базис в том же образовывать базис в том же  ? [4, с. 38] ? [4, с. 38] 3. Пусть векторы  и и  образуют базис в образуют базис в  . Система векторов . Система векторов  , ,  линейно независима в том же линейно независима в том же  . Найти разложение в базисе . Найти разложение в базисе  , ,  векторов векторов  и и  [4, с. 38] [4, с. 38] 4. Доказать, что система векторов  , ,  и и  линейно зависима. [4, с. 42] линейно зависима. [4, с. 42] 5. Даны векторы  , ,  и и  . Выразить вектор . Выразить вектор  через векторы через векторы  и и  . [4, с. 42] . [4, с. 42] 6. Выяснить образуют ли базис в  векторы: а) векторы: а)  , ,  ; б) ; б)  ; ;  . [4, с. 43] . [4, с. 43] 7. Найти все значения параметра 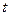 , при котором векторы , при котором векторы  , , 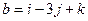 , ,  образуют базис в образуют базис в  . [4, с. 43] . [4, с. 43] 8. Доказать, что векторы  , ,  и и  линейно зависимы. Выразить: а) вектор линейно зависимы. Выразить: а) вектор  через векторы через векторы  и и  ; б) вектор ; б) вектор  через векторы через векторы  и и  ; в) вектор ; в) вектор  через векторы через векторы  и и  . . 9. Доказать, что векторы  , ,  и и  линейно зависимы. Можно ли выразить вектор линейно зависимы. Можно ли выразить вектор  через векторы через векторы  и и  ? ? 10. Выяснить, образуют ли базис в  векторы: a) векторы: a)  , ,  ; б) ; б)  , ,  . . 11. Найти все значения параметра при которых векторы  , ,  , ,  образуют базис в образуют базис в  . . 12. На плоскости даны три вектора 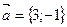 , ,  и и  . Определить разложение каждого из трех векторов, принимая в качестве базиса два других. . Определить разложение каждого из трех векторов, принимая в качестве базиса два других. Аналитические задачи 1. Показать, что если сумма 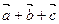 трех ненулевых векторов трех ненулевых векторов  , ,  и и  равна нуль-вектору, то из этих векторов можно составить треугольник. [2, с. 80] равна нуль-вектору, то из этих векторов можно составить треугольник. [2, с. 80] 2. Показать, что система двух векторов линейно зависима тогда и только тогда, когда вектора коллинеарны. [3, с. 75] 3. Доказать, что система трёх матриц 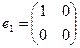 , ,  , ,  линейно независима. [5, с. 35] линейно независима. [5, с. 35] 4. Известно, что векторы  , ,  , …, , …,  образуют базис. Является ли базисом система векторов образуют базис. Является ли базисом система векторов  , ,  ,…, ,…,  , где , где  - числа, не равные нулю? Ответ обоснуйте. - числа, не равные нулю? Ответ обоснуйте. 5. Показать, что система любых четырёх векторов в пространстве линейно зависима. [4, с. 31] 6. Показать, что система трёх векторов линейно независима тогда и только тогда, когда векторы отличны от нуля и не существует параллельной им плоскости. [3, с. 75] 7. Показать, что система любых трёх компланарных векторов, лежащих в одной плоскости, всегда линейно зависима. [3, с. 75] 8. Показать, что если система векторов  и и  в плоскости линейно независима, то любой вектор в плоскости линейно независима, то любой вектор  в этой плоскости линейно выражается через в этой плоскости линейно выражается через  и и  : :  . Числа . Числа  и и 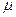 определяются однозначно. [3, с. 76] определяются однозначно. [3, с. 76] 9. Показать, что если система трёх векторов  , ,  и и 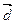 линейно независима, то любой вектор линейно независима, то любой вектор  через данные вектора однозначно выражается в виде: через данные вектора однозначно выражается в виде:  . [3, с. 76] . [3, с. 76] 10. Показать, что система трёх векторов  , , 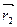 , ,  линейно независима тогда и только тогда, когда для указанных векторов выполняется условие линейно независима тогда и только тогда, когда для указанных векторов выполняется условие  . [3, с. 78] . [3, с. 78]
11. Доказать, что система трёх векторов линейно зависима, если среди этих векторов есть нуль-вектор. [4, с. 42] 12. Доказать, что если  - трапеция, то система векторов - трапеция, то система векторов 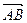 , ,  , ,  линейно зависима. [4, с. 42] линейно зависима. [4, с. 42] 13. Зная векторы  и и  , на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной стороне , на которых построен параллелограмм, выразить через них вектор, совпадающий с высотой параллелограмма, перпендикулярной стороне  . [2, с. 98] . [2, с. 98] 14. Доказать, что равновесие точки невозможно под действием: а) двух неколлинеарных сил; б) трех некомпланарных сил. Скалярное произведение Геометрические задачи 1. В треугольнике  угол при вершине угол при вершине  равен равен  , а длина стороны , а длина стороны  в три раза больше расстояния между вершинами в три раза больше расстояния между вершинами  и и 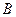 . Найти острый угол . Найти острый угол  между стороной между стороной  и медианой и медианой  треугольника. [1, с. 52] треугольника. [1, с. 52] 2. В треугольнике  угол при вершине угол при вершине  равен равен  , ,  , ,  . Найти угол между медианой и биссектрисой, которые проведены из вершины . Найти угол между медианой и биссектрисой, которые проведены из вершины  . [1, с. 76] . [1, с. 76] 3.  - правильный шестиугольник со стороной 2. Найти скалярное произведение векторов - правильный шестиугольник со стороной 2. Найти скалярное произведение векторов  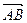 и и  . [2, с. 94] . [2, с. 94] 4. Диагональ параллелепипеда соединяет вершины  и и  , не принадлежащие одной грани. Ребра параллелепипеда, выходящие из вершины , не принадлежащие одной грани. Ребра параллелепипеда, выходящие из вершины  , имеют длины , имеют длины  , ,  , ,  , а углы между ребрами имеет следующие значения: , а углы между ребрами имеет следующие значения:  (между (между  и и  ), ),  (между (между  и и  ), ),  (между (между  и и  ). Найти длину диагонали. [4, с. 39] ). Найти длину диагонали. [4, с. 39] 5. Чему равен косинус угла между диагональю куба и его ребром? [4, с. 45] 6. Вычислить тупой угол, образованный медианами, проведенными из вершин равнобедренного треугольника. Алгебраические задачи 1. Найти длину вектора  при условии, что при условии, что  , ,  , а угол между векторами , а угол между векторами  и и 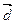 равен равен  . [1, с. 52] . [1, с. 52] 2. Найти угол между векторами  и и  , если известно, что , если известно, что  , , 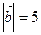 и угол между векторами и угол между векторами  и и  равен равен  . [1, с. 76] . [1, с. 76] 3. Найти значения параметра 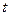 , при которых векторы , при которых векторы  и и  имеют одинаковую длину. [1, с. 76] имеют одинаковую длину. [1, с. 76] 4. Найти значения параметра 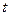 , при которых векторы , при которых векторы  и и  , заданные своими координатами в ортонормированном базисе, ортогональны. [1, с. 55] , заданные своими координатами в ортонормированном базисе, ортогональны. [1, с. 55] 5. Найти работу силы  при перемещении материальной точки на вектор при перемещении материальной точки на вектор  . [1, с. 76] . [1, с. 76] 6. Вычислить длины диагоналей параллелограмма, построенного на векторах  и и  , где , где 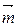 и и  - единичные вектора, величина угла между которыми - единичные вектора, величина угла между которыми  . [2, с. 95] . [2, с. 95] 7. Даны векторы 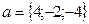 и и  . Вычислить скалярное произведение векторов . Вычислить скалярное произведение векторов  и и  . [2, с. 96] . [2, с. 96] 8. Даны вершины треугольника  , ,  и и  . Определить величину его внутреннего угла при вершине . Определить величину его внутреннего угла при вершине 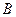 . [2, с. 96] . [2, с. 96] 9. Вычислить работу, которую производит сила  , когда её точка приложения, двигаясь прямолинейно, перемещается из положения , когда её точка приложения, двигаясь прямолинейно, перемещается из положения  в положение в положение  . [2, с. 98] . [2, с. 98] 10. Найти вектор  , коллинеарный вектору , коллинеарный вектору  и удовлетворяющий условию и удовлетворяющий условию  . [2, с. 98] . [2, с. 98] 11. Найдите угол между биссектрисами координатных углов  и и  . [4, с. 45] . [4, с. 45] 12. Дано, что 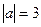 , ,  . Определить, при каком значении . Определить, при каком значении  векторы векторы  , ,  будут взаимно перпендикулярны. будут взаимно перпендикулярны. 13. Вычислив внутренние углы треугольника с вершинами  , ,  , ,  , убедиться, что этот треугольник равнобедренный. , убедиться, что этот треугольник равнобедренный. Аналитические задачи 1. Проверить справедливость равенства 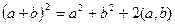 .[2, с. 97] .[2, с. 97] 2. Проверить справедливость равенства  . [2, с. 97] . [2, с. 97] 3. Доказать, что уравнение  определяет сферу с центром определяет сферу с центром  и радиусом и радиусом  . [2, с. 98] . [2, с. 98] 4. Доказать, что  . [2, с. 98] . [2, с. 98] 5. Даны единичные векторы  , ,  и и  , удовлетворяющие условию , удовлетворяющие условию 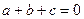 . Вычислить . Вычислить 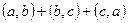 . [2, с. 98] . [2, с. 98] 6. Какой угол составляют между собой векторы 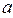 и и  , если известно, что вектор , если известно, что вектор  ортогонален вектору ортогонален вектору  , а вектор , а вектор  ортогонален вектору ортогонален вектору  ? [2, с. 98] ? [2, с. 98] 7. Вычислить тупой угол, образованный медианами, проведенными из вершин равнобедренного прямоугольного треугольника. [2, с. 98] 8. Докажите, что треугольник с вершинами 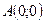 , ,  , ,  - прямоугольный. [4, с. 45] - прямоугольный. [4, с. 45] 9. Докажите, что треугольник с вершинами  , , 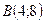 , ,  - тупоугольный. [4, с. 45] - тупоугольный. [4, с. 45] 10. Докажите, что вектор  перпендикулярен вектору перпендикулярен вектору  . [4, с. 45] . [4, с. 45] 11. Какому условию должны удовлетворять векторы  и и  , чтобы вектор , чтобы вектор  был перпендикулярен к вектору был перпендикулярен к вектору  ? ? Векторное произведение Алгебраические задачи 1. Найти площадь треугольника, построенного на векторах  и и  . [1, с. 76] . [1, с. 76] 2. Сила  приложена к точке приложена к точке  . Определить момент этой силы относительно точки . Определить момент этой силы относительно точки  .[2, с. 106] .[2, с. 106] 3. Вычислить площадь параллелограмма, построенного на векторах  и и  , где , где  и и  - единичные векторы, величина угла между которыми - единичные векторы, величина угла между которыми  . [2, с. 107] . [2, с. 107] 4. Найти единичный вектор  , перпендикулярный каждому из векторов , перпендикулярный каждому из векторов  и и  . [2, с. 107] . [2, с. 107] 5. Найти единичный вектор  , одновременно перпендикулярный вектору , одновременно перпендикулярный вектору  и оси абцисс. [2, с. 107] и оси абцисс. [2, с. 107] 6. Векторы  и и  образуют угол образуют угол  . Зная, что . Зная, что  , ,  , вычислить , вычислить  . . 7. Векторы  и и  взаимо перпендикулярны. Зная, что взаимо перпендикулярны. Зная, что 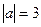 , ,  , вычислить , вычислить 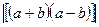 . . 8. Даны векторы  и и  . Найти координаты векторных произведений: 1) . Найти координаты векторных произведений: 1)  ; 2) ; 2)  . . Аналитические задачи 1. Найти все векторы, ортогональные векторам  и и  . [1, с. 65] . [1, с. 65] 2. Найти угол между ненулевыми векторами  и и  , если они удовлетворяют соотношению , если они удовлетворяют соотношению  . [1, с. 76] . [1, с. 76] 3. Векторы  , ,  , ,  некомпланарны, а векторы некомпланарны, а векторы 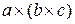 и и  коллиниарны. Найти угол между векторами коллиниарны. Найти угол между векторами  и и  . [1, с. 76] . [1, с. 76] 4. Доказать компланарность векторов  , ,  , ,  . . 5. Показать, что если векторы 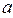 и и  перпендикулярны вектору перпендикулярны вектору  , то , то  . [3, с. 80] . [3, с. 80] 6. Доказать тождество  . . 7. Векторы  , ,  , ,  удовлетворяют условию удовлетворяют условию  . Доказать, что . Доказать, что  . . 8. Векторы  , ,  , ,  и и  связаны соотношениями связаны соотношениями  , ,  . Доказать, коллинеарность векторов . Доказать, коллинеарность векторов  и и  . . Смешанное произведение Алгебраические задачи 1. Найти объём треугольной пирамиды, построенной на векторах  , ,  и и  как на смежных рёбрах. [1, с. 70] как на смежных рёбрах. [1, с. 70] 2. При каких значениях 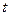 векторы векторы  , ,  , ,  компланарны. [1, с. 76] компланарны. [1, с. 76] 3. Вычислить объем тетраэдра, вершины которого находятся в точках  , ,  , ,  и и  . [2, с. 110] . [2, с. 110] 4. Вектор  перпендикулярен векторам перпендикулярен векторам  и и  , величина угла между которыми равна 30°. Зная, что , величина угла между которыми равна 30°. Зная, что  , ,  , вычислить , вычислить  . [2, с. 111] . [2, с. 111] 5. Вычислить высоту параллелепипеда, построенного на векторах  , ,  , ,  . За основание взят параллелограмм, построенный на векторах . За основание взят параллелограмм, построенный на векторах  и и  . [2, с. 111] . [2, с. 111] 6. Объем тетраэдра равен  , три его вершины находятся в точках , три его вершины находятся в точках  , ,  , ,  . Найти координаты четвертой вершины. . Найти координаты четвертой вершины. Аналитические задачи 1. Доказать компланарность векторов  , ,  , ,  . . 2. Определить какой является тройка ортов  , ,  , ,  прямоугольной декартовой системы координат прямоугольной декартовой системы координат  . [2, с. 110] . [2, с. 110] 3. Вычислить произведение  . [2, с. 110] . [2, с. 110] 4. Вычислить произведение  , если , если  . [2, с. 111] . [2, с. 111] 5. Вывести условие принадлежности четырех точек  | 



 на плоскости и постройте:
на плоскости и постройте: ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
. треугольника
треугольника  разделена точками
разделена точками  и
и  на три равные части. Обозначив
на три равные части. Обозначив  и
и  , выразите через
, выразите через  и
и  векторы
векторы  и
и  .
. имеем
имеем  и
и  . Выразите через
. Выразите через  и
и 


 где
где  треугольника
треугольника  так, что прямая
так, что прямая  -биссектриса угла при вершине
-биссектриса угла при вершине  . Выразите через
. Выразите через  и
и  следующие векторы:
следующие векторы: 
 соединена с серединой
соединена с серединой  . Найдите, в каком отношении отрезок
. Найдите, в каком отношении отрезок  делит диагональ
делит диагональ  .
. заданы векторы, совпадающие с его сторонами
заданы векторы, совпадающие с его сторонами  ,
,  ,
,  ,
,  ,
,  . Построить векторы 1)
. Построить векторы 1) 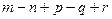 ; 2)
; 2)  ; 3)
; 3)  .
. заданы векторы, совпадающие с его ребрами
заданы векторы, совпадающие с его ребрами  и
и  . Построить следующие векторы: 1)
. Построить следующие векторы: 1)  ; 2)
; 2) 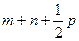 ; 3)
; 3)  .
. ; б)
; б) 
 , через векторы
, через векторы  и
и 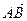 .
. , если отложить его от того же начала, будет направлен по биссектрисе угла между
, если отложить его от того же начала, будет направлен по биссектрисе угла между  является центром масс треугольника
является центром масс треугольника 
 если отложить его от того же начала, будет направлен по биссектрисе угла между
если отложить его от того же начала, будет направлен по биссектрисе угла между  . В каком случае левая часть равна правой?
. В каком случае левая часть равна правой? ; б)
; б)  ; в)
; в) 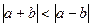 ?
? Докажите, что сумма векторов
Докажите, что сумма векторов  равна нулю. Как обобщить эту задачу на случай
равна нулю. Как обобщить эту задачу на случай  - угольника?
- угольника? и
и 
 ,
,  ,
,  .
. и
и  коллинеарны векторы:
коллинеарны векторы: ,
,  ; б)
; б) 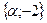 ,
,  .
. Проверьте, что четырехугольник
Проверьте, что четырехугольник  . Найдите четвертую точку
. Найдите четвертую точку  являются вершинами трапеции.
являются вершинами трапеции. ,
,  и
и  . Вычислить
. Вычислить  .
. и
и  . Определить
. Определить  .
. , причем
, причем  . Определить
. Определить  ,
, 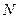 и
и  , если известно, что
, если известно, что  ,
,  и
и 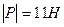 .
. и
и  приложены к одной точке. Определить координаты вектора
приложены к одной точке. Определить координаты вектора  .
. ,
,  и
и  углы, равные соответственно: а) 120°, 135°, 45°; б) 120°, 135°, 60°.
углы, равные соответственно: а) 120°, 135°, 45°; б) 120°, 135°, 60°. имеет длину, равную 5, и образует с вектором
имеет длину, равную 5, и образует с вектором 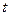 при которых вектор
при которых вектор  a) образует с вектором
a) образует с вектором  ; в) является противоположно направленным вектору
; в) является противоположно направленным вектору  .
. ,
,  в базисе
в базисе  ,
,  ,
,  . [1, с. 19]
. [1, с. 19] имеем
имеем  и
и 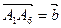 . Разложите по базису
. Разложите по базису  ,
,  векторы
векторы  ,
,  ,
,  . [1, с. 27]
. [1, с. 27] ,
,  ,
,  , приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину равнодействующей
, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину равнодействующей  , если известны величины сил
, если известны величины сил 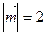 ,
, 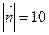 ,
,  . [2, с. 81]
. [2, с. 81] ), направленного с северо-запада под углом
), направленного с северо-запада под углом 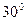 к северу, на компоненты, имеющие направления на север и запад. [2, с. 81]
к северу, на компоненты, имеющие направления на север и запад. [2, с. 81] и
и  . Разложить по этим двум векторам все векторы, совпадающими со сторонами ромба:
. Разложить по этим двум векторам все векторы, совпадающими со сторонами ромба:  . [2, с. 82]
. [2, с. 82] ,
,  ,
,  . Выразить через эти векторы остальные ребра тетраэдра, медиану
. Выразить через эти векторы остальные ребра тетраэдра, медиану  , грани
, грани  и вектор
и вектор 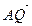 , где
, где  – центр тяжести грани
– центр тяжести грани 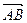 ,
,  ,
,  образовывать базис в пространстве
образовывать базис в пространстве  ?
? треугольника
треугольника 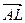 в базисе
в базисе  ,
,  образовывать базис в
образовывать базис в  ? Ответ обосновать.
? Ответ обосновать.
 ,
, 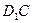 ,
,  .
. и
и  принадлежат соответственно прямым
принадлежат соответственно прямым  и
и  , которые пересекаются в некоторой точке
, которые пересекаются в некоторой точке  и
и  векторы, направленные по биссектрисам углов между прямыми. [1, с. 76]
векторы, направленные по биссектрисам углов между прямыми. [1, с. 76]  . Точки
. Точки  и
и  и
и  . Выразить вектор
. Выразить вектор 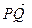 через векторы
через векторы  ,
, 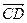 . [1, с. 10]
. [1, с. 10]  соответственно. Найти координаты вектора
соответственно. Найти координаты вектора  и
и  . [1, с. 15]
. [1, с. 15]  имеем
имеем  и
и  . Разложить по базису
. Разложить по базису  векторы
векторы 
 и
и  на плоскости не коллинеарны, и разложить вектор
на плоскости не коллинеарны, и разложить вектор  по базису
по базису  и
и  образуют базис в
образуют базис в  ,
,  образовывать базис в том же
образовывать базис в том же  [4, с. 38]
[4, с. 38] ,
,  и
и  линейно зависима. [4, с. 42]
линейно зависима. [4, с. 42] через векторы
через векторы  ,
,  ; б)
; б)  ;
;  . [4, с. 43]
. [4, с. 43] ,
, 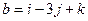 ,
,  образуют базис в
образуют базис в  ,
,  и
и  линейно зависимы. Выразить: а) вектор
линейно зависимы. Выразить: а) вектор  через векторы
через векторы  ,
,  линейно зависимы. Можно ли выразить вектор
линейно зависимы. Можно ли выразить вектор  векторы: a)
векторы: a)  ,
,  ; б)
; б)  ,
,  .
. ,
,  ,
,  образуют базис в
образуют базис в 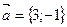 ,
,  и
и  . Определить разложение каждого из трех векторов, принимая в качестве базиса два других.
. Определить разложение каждого из трех векторов, принимая в качестве базиса два других.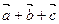 трех ненулевых векторов
трех ненулевых векторов 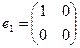 ,
,  ,
,  линейно независима. [5, с. 35]
линейно независима. [5, с. 35] образуют базис. Является ли базисом система векторов
образуют базис. Является ли базисом система векторов  ,
,  ,…,
,…,  , где
, где  - числа, не равные нулю? Ответ обоснуйте.
- числа, не равные нулю? Ответ обоснуйте. . Числа
. Числа  и
и 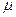 определяются однозначно. [3, с. 76]
определяются однозначно. [3, с. 76]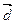 линейно независима, то любой вектор
линейно независима, то любой вектор  . [3, с. 76]
. [3, с. 76] ,
, 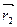 ,
,  линейно независима тогда и только тогда, когда для указанных векторов выполняется условие
линейно независима тогда и только тогда, когда для указанных векторов выполняется условие . [3, с. 78]
. [3, с. 78] линейно зависима. [4, с. 42]
линейно зависима. [4, с. 42] , а длина стороны
, а длина стороны  между стороной
между стороной  треугольника. [1, с. 52]
треугольника. [1, с. 52] ,
,  ,
,  . Найти угол между медианой и биссектрисой, которые проведены из вершины
. Найти угол между медианой и биссектрисой, которые проведены из вершины  - правильный шестиугольник со стороной 2. Найти скалярное произведение векторов
- правильный шестиугольник со стороной 2. Найти скалярное произведение векторов 
 . [2, с. 94]
. [2, с. 94] (между
(между  при условии, что
при условии, что  ,
,  , а угол между векторами
, а угол между векторами  . [1, с. 52]
. [1, с. 52] и
и  , если известно, что
, если известно, что  ,
, 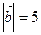 и угол между векторами
и угол между векторами  и
и  имеют одинаковую длину. [1, с. 76]
имеют одинаковую длину. [1, с. 76] и
и  , заданные своими координатами в ортонормированном базисе, ортогональны. [1, с. 55]
, заданные своими координатами в ортонормированном базисе, ортогональны. [1, с. 55] при перемещении материальной точки на вектор
при перемещении материальной точки на вектор  . [1, с. 76]
. [1, с. 76] и
и  , где
, где 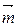 и
и  . [2, с. 95]
. [2, с. 95]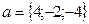 и
и  . Вычислить скалярное произведение векторов
. Вычислить скалярное произведение векторов  и
и  . [2, с. 96]
. [2, с. 96] ,
,  и
и  . Определить величину его внутреннего угла при вершине
. Определить величину его внутреннего угла при вершине  , когда её точка приложения, двигаясь прямолинейно, перемещается из положения
, когда её точка приложения, двигаясь прямолинейно, перемещается из положения  в положение
в положение  . [2, с. 98]
. [2, с. 98] , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию  . [2, с. 98]
. [2, с. 98] и
и  . [4, с. 45]
. [4, с. 45]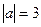 ,
,  . Определить, при каком значении
. Определить, при каком значении  ,
,  будут взаимно перпендикулярны.
будут взаимно перпендикулярны. ,
,  ,
,  , убедиться, что этот треугольник равнобедренный.
, убедиться, что этот треугольник равнобедренный.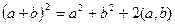 .[2, с. 97]
.[2, с. 97] . [2, с. 97]
. [2, с. 97] определяет сферу с центром
определяет сферу с центром  и радиусом
и радиусом  . [2, с. 98]
. [2, с. 98]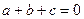 . Вычислить
. Вычислить 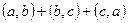 . [2, с. 98]
. [2, с. 98]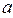 и
и  ортогонален вектору
ортогонален вектору  , а вектор
, а вектор  ортогонален вектору
ортогонален вектору  ? [2, с. 98]
? [2, с. 98]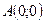 ,
,  ,
,  - прямоугольный. [4, с. 45]
- прямоугольный. [4, с. 45] ,
, 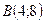 ,
,  - тупоугольный. [4, с. 45]
- тупоугольный. [4, с. 45] перпендикулярен вектору
перпендикулярен вектору  . [4, с. 45]
. [4, с. 45] ?
? и
и  . [1, с. 76]
. [1, с. 76] приложена к точке
приложена к точке  . Определить момент этой силы относительно точки
. Определить момент этой силы относительно точки  .[2, с. 106]
.[2, с. 106] и
и  , где
, где  и
и  - единичные векторы, величина угла между которыми
- единичные векторы, величина угла между которыми  . [2, с. 107]
. [2, с. 107] , перпендикулярный каждому из векторов
, перпендикулярный каждому из векторов  и
и  . [2, с. 107]
. [2, с. 107] и оси абцисс. [2, с. 107]
и оси абцисс. [2, с. 107] . Зная, что
. Зная, что  ,
,  .
. , вычислить
, вычислить 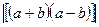 .
. и
и  . Найти координаты векторных произведений: 1)
. Найти координаты векторных произведений: 1)  ; 2)
; 2)  .
. и
и  . [1, с. 65]
. [1, с. 65] . [1, с. 76]
. [1, с. 76] ,
,  ,
,  некомпланарны, а векторы
некомпланарны, а векторы 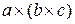 и
и  ,
,  ,
,  .
. , то
, то  . [3, с. 80]
. [3, с. 80] .
. ,
,  . Доказать, что
. Доказать, что  .
. связаны соотношениями
связаны соотношениями  ,
,  . Доказать, коллинеарность векторов
. Доказать, коллинеарность векторов  и
и  .
. ,
,  и
и  как на смежных рёбрах. [1, с. 70]
как на смежных рёбрах. [1, с. 70] ,
,  ,
,  компланарны. [1, с. 76]
компланарны. [1, с. 76] ,
,  ,
,  и
и  . [2, с. 110]
. [2, с. 110] и
и  , величина угла между которыми равна 30°. Зная, что
, величина угла между которыми равна 30°. Зная, что  , вычислить
, вычислить  . [2, с. 111]
. [2, с. 111] ,
,  ,
,  . За основание взят параллелограмм, построенный на векторах
. За основание взят параллелограмм, построенный на векторах  , три его вершины находятся в точках
, три его вершины находятся в точках  ,
,  ,
,  . Найти координаты четвертой вершины.
. Найти координаты четвертой вершины. .
. ,
,  ,
, 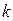 прямоугольной декартовой системы координат
прямоугольной декартовой системы координат  . [2, с. 110]
. [2, с. 110] . [2, с. 110]
. [2, с. 110] , если
, если  . [2, с. 111]
. [2, с. 111]