 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
Контрольная работа по дисциплине «Математика» Для студентов «Государственное и муниципальное направление» Заочного обучения
1.Вычислить определитель:
1.1. a. 1.2. a. 1.3. a. 1.4 a. 1.5 . a. 1.6. a. 1.7. a. 1.8. a. 1.9. a. 1.10. a. 2.Решить уравнение:
2.1. 2.3. 2.5. 2.7.
2.9. 3.Вычислить определитель, пользуясь правилом треугольника:
3.1. 3.4. 3.7. 3.10. 4.Вычислить определитель, предварительно обратив в нуль все, кроме одного, элементы какой-нибудь строки (столбца) :
4.1.
4.3.
4.5.
4.7.
4.9.
5.Решить систему уравнений с помощью правила Крамера :
5.1.
5.3.
5.5.
5.7.
5.9
6.Умножить матрицы:
6.1. a. 6.2. a. 6.3. a. 6.4. a. 6.5. a. 6.6. a. 6.7. a. 6.8. a. 6.9. a. 6.10. a. 7.Найти обратные матрицы для следующих матриц:
8.1. 8.3. 8.5.
8.7. 8.9. 9.Решить методом Гаусса системы уравнений: 9.1.
9.3.
9.5. 9.7.
9.9. 10.Вычислить пределы:
10.1. a.
10.2. a.
10.3. a. 10.4. a. 10.5. a. 10.6. a. 10.7. a. 10.8. a. 10.9. a. 10.10. a.
11.Вычислить производную функции: 11.1.
11.3.
11.5. 11.7. 11.9. 12. Провести полное исследование функции и построить ее график:
12.1. 12.3. 12.5. 12.7. 12.9.
Вариант 1 1. Какова вероятность того, что при 10 бросках игральной кости 5 очков выпадет не более 2-ух раз?
2. В магазин поступают часы с трех заводов, соответственно 40%, 45% и 15%. В продукции первого завода идут точно 80% часов, второго – 70% и третьего – 90%. Какова вероятность того, что купленные часы идут точно?
3. Вероятность рождения мальчика – 0,51, девочки – 0,49. В семье 5 детей. Найти вероятность того, что среди них не более двух девочек.
4. Пять работниц окрашивают одинаковые игрушки: две в красный цвет, а три – в зеленый. Производительность труда работниц одинаковая. Окрашенные игрушки складываются в один ящик. Определить вероятность того, что среди 600 игрушек красных окажется от 228 до 264.
5. Установлено, что в среднем 0,25% шариков, изготовленных для подшипников, оказывается бракованными. Составить ряд и функцию распределения случайной величины X - числа бракованных шариков среди пяти проверенных.
6. Дискретная случайная величина X имеет два значения
Вариант 2 1. Наугад указывается месяц и число не високосного года. Какова вероятность того, что это будет воскресенье, если в этом году их всего 53? 2. Из 10 деталей 4 окрашены. Вероятность того, что окрашенная деталь тяжелее нормы равна 0,3, а неокрашенная – 0,1. Найти вероятность того, что взятая наудачу деталь окажется тяжелее нормы.
3. По цели производится 5 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,4. Для получения зачета по стрельбе требуется не менее трех попаданий. Найти вероятность получения зачета.
4. Вероятность выпуска сверла повышенной хрупкости равна 0,02. Сверла укладываются в коробки по 100 штук. Найти вероятность того, что бракованных сверл окажется не более трех. 5. Построить ряд и функцию распределения случайной величины X – числа попаданий в цель стрелком при трех выстрелах, если вероятность попадания при одном выстреле равна 0,8.
6. Дискретная случайная величина принимает два значения
Вариант 3
1. В коробке лежит 5 белых и 8 черных шаров. Наудачу вынимают 3 шара. Какова вероятность что: а) среди них два белых; б) что они одного цвета?
2. Вся продукция проверяется двумя контролерами. Вероятность того, что изделие проверит первый контролер, равна – 0,55, второй – 0,45. Вероятности того, что контролеры пропустят нестандартное изделие, равны 0,01 и 0,02 соответственно. Какова вероятность того, что наудачу выбранное изделие окажется бракованным?
3. Прядильщица обслуживает 30 веретен. Вероятность обрыва нити на одном веретене в течение минуты равна 0,2. Найти вероятность того, что в течение 1 минуты обрыв произойдет не менее чем на 5-ти, но не более, чем на 7 веретенах.
4. Найти вероятность того, что событие А наступит 1400 раз при 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.
5. Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Написать ряд и функцию распределения случайной величины X – числа стандартных деталей среди трех наудачу выбранных.
6. Даны независимые случайные величины Х и Y:
Найти неизвестные значения
Вариант 4
1. Три стрелка стреляют в цель независимо друг от друга. Первый стрелок попадает в цель с вероятностью 0,6, второй - с вероятностью 0,7, а третий - с вероятностью 0,75. Найти вероятность хотя бы одного попадания в цель, если каждый стрелок делает по одному выстрелу.
2. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная, во втором - 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартная.
3. Вероятность того, что дошкольник не посещает детский сад, равна 0,2. Какова вероятность, что из 9 наудачу выбранных дошкольников не менее 6 посещают детский сад?
4. Монету бросают 400 раз. Какова вероятность того, что “герб” выпадет не менее 204 раз и не более 214 раз?
5. В партии хлопка 20% коротких волокон. Построить ряд и функцию распределения случайной величины X - числа коротких волокон среди трех отобранных.
6. Дискретная случайная величина принимает два значения
Вариант 5
1. В тире имеется 3 ружья, вероятности попадания из которых равны соответственно 0,7, 0,8 и 0,9. Определить вероятность попадания при одном выстреле, если стрелок берет ружье наугад.
2. В магазин поступают часы с 3-х заводов, соответственно 40%, 45% и 15%. В продукции 1-го завода идут точно 80% часов, 2-го - 70% и 3-го - 90%. Какова вероятность, что купленные часы идут точно.
3. Вероятность появления некоторого события в каждом из 18 независимых опытов равна 0,2. Определить вероятность появления этого события хотя бы 3 раза.
4. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.
5. Вероятность наличия нужного товара в первом магазине равна 0,8, во втором – 0,75, в третьем -0,7. Покупатель в указанной последовательности посещает эти магазины до тех пор, пока не найдет нужный ему товар. Составить закон распределения случайной величины Х – число посещенных магазинов.
6. Даны независимые случайные величины Х и Y:
Найти неизвестные значения
Вариант 6
1. В группе 10 человек: 7 юношей и 3 девушки. На дежурство заступает 4 человека, Какова вероятность, что это 2 девушки и 2 юноши?
2. Игральная кость бросается 5 раз. Найти вероятность того, что два раза появится число очков, кратное трем.
3. При установившемся технологическом процессе происходит 10 обрывов нити на 100 станках в час. Определить вероятность того, что на 80 станках в течение часа нить порвется не более 2 раз.
4. Из пяти гвоздик две белые. Составить закон распределения случайной величины Х – число белых гвоздик среди двух одновременно наугад взятых. Найти функцию распределения этой случайной величины.
5. Среди семи электроламп имеются четыре неисправных. Наудачу одновременно выбирают три лампы. Составить закон распределения случайной величины Х – число неисправных ламп среди отобранных. Найти функцию распределения этой случайной величины.
6. Даны независимые случайные величины Х и Y:
Найти неизвестные значения
Вариант 7 1. В ящике лежат 15 красных, 9 синих и 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что вынутыми окажутся – 1 зеленый, 2 синих и и3 красных шара.
2. В соревновании участвуют 4 студента из 1-ой группы, 6 – из 2-ой и 5 – из 3-ей. Студенты могут попасть в сборную института с вероятностями 0,9, 0,8 и 0,7 соответственно. Какова вероятность того, что наудачу выбранный студент попадёт в сборную?
3. Вероятность отказа каждого прибора при испытании равна 0,2. Какова вероятность того, что при испытаниях из 10 приборов будет работать не менее 2-х приборов?
4. Всхожесть хранящегося на складе зерна равна 80%. Отбираются 400 зерен. Определить вероятность того, что из отобранных зерен взойдут: ровно 303 зерна.
5. В магазине продаются пять отечественных и три импортных телевизора. Составить закон распределения случайной величины Х – числа импортных телевизоров из четырёх наудачу выбранных телевизоров. Найти функцию распределения этой случайной величины.
6. Математическое ожидание случайной величины Х равно 1,5. Закон распределения задан таблицей:
Найти значения Вариант 8
1. В группе 25 студентов. Из них отлично успевают по математике 5 человек, хорошо - 12 человек, удовлетворительно - 6 человек. Наудачу выбирается 6 студентов. Какова вероятность, что 4 из них отличники и 2 хорошисты?
2. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника- 0,9, для велосипедиста – 0,8 и для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
3. В камере хранения 80% всей клади составляют чемоданы. Получены все вещи с одной полки с количеством мест равным 15. Найти вероятность, что среди выданных вещей не более 3 чемоданов.
4. Ожидается прибытие трех судов с фруктами. Статистика показывает, что 1% судов привозят товар, не пригодный к употреблению. Найти вероятность того, что хотя бы два судна привезут качественный товар.
5. Вероятность правильного решения первой задачи равна 0,9 и уменьшается с каждой следующей задачей на 0,1. Составить закон распределения случайной величины Х – число правильно решенных задач среди трех предложенных. Найти функцию распределения этой случайной величины.
6. Даны независимые случайные величины Х и Y:
Найти неизвестные значения
Вариант 9
1. В магазин поступило 60 пар обуви:26 пар коричневого цвета,22-красного и 12 пар синего. Какова вероятность, что наудачу взятая коробка окажется с обувью синего цвета?
2. Из пункта А ведут 4 дороги в пункты CI, С2, СЗ и С4, из которых можно прийти в пункт В с вероятностями 1/3, 1/2, 1, 2/5 соответственно. Какова вероятность, что туристы, выйдя из пункта А, дойдут в пункт В?
3. Вероятность того, что страховой договор завершиться выплатой, оценивается как 0,2. Найти вероятность того, что из 20 договоров выплатой завершится хотя бы один из них.
4. Вероятность того, что телевизор выдержит гарантийный срок работы, равна 0,8. Найти вероятность того, что из 1000 выпущенных телевизоров количество, выдержавших гарантийный срок службы, находится в пределах от 600 до 950.
5. В среднем 10% фермеров не получают запланированного дохода. Составить закон распределения случайной величины Х – число фермеров, получивших желаемый доход, из четырех наудачу выбранных. Найти функцию распределения этой случайной величины.
6. Математическое ожидание случайной величины Х равно 2,3. Закон распределения задан таблицей:
Найти значения Вариант 10
1. В мастерскую для ремонта поступили 20 часов. Известно, что 6 их них можно отремонтировать. Мастер берет любых 5 часов. Определить вероятность того, что двое из них можно отремонтировать.
2. В таксопарке число новых машин и старых относится как 3:5. Вероятность поломки новой машины 0,25, а старой — 0,4. Какова вероятность, что машина на линии сломается?
3. Вероятность того, что компьютер в магазине имеет дефект, равна 0,15. Найти вероятность того, что из 20 компьютеров не более одного имеют дефект.
4. Фабрика выпускает 75% продукции 1-го сорта. Чему равна вероятность того, что из 300 изделий число изделий первого сорта заключено между 219 и 234?
5. Клиенты банка не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения случайной величины Х – число возвращенных кредитов из четырех выданных. Найти функцию распределения этой случайной величины.
6. Дискретная случайная величина принимает два значения
Приложение 1 ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ |



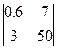 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 2.2.
2.2. 
 2.4.
2.4. 
 2.6.
2.6. 
 2.8.
2.8. 
 2.10.
2.10. 
 3.2.
3.2.  3.3.
3.3. 
 3.5.
3.5.  3.6.
3.6. 
 3.8.
3.8.  3.9.
3.9. 

 4.2.
4.2. 
 4.4.
4.4. 
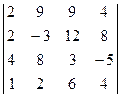 4 .6.
4 .6. 
 4.8.
4.8. 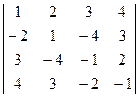
 4.10.
4.10. 
 5.2.
5.2. 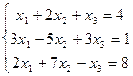
 5.4.
5.4. 
 5.6.
5.6. 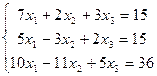
 5.8.
5.8. 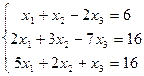
 5.10.
5.10. 
 b.
b. 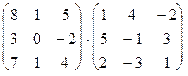
 b.
b. 
 b.
b. 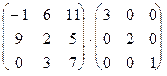
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
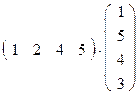 b.
b. 
 b.
b. 
 b.
b. 
 8.2.
8.2. 
 8.4.
8.4. 
 8.6.
8.6. 
 8.8.
8.8. 
 8.10.
8.10. 
 9.2.
9.2. 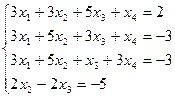
 9.4.
9.4. 
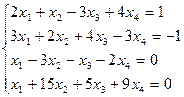 9.6.
9.6. 
 9.8.
9.8. 
 9.10.
9.10. 
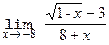 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 

 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 b.
b. 
 11.2.
11.2. 
 11.4.
11.4. 
 11.6.
11.6. 
 11.8.
11.8. 
 11.10
11.10 
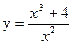 12.2.
12.2. 
 12.4.
12.4. 
 12.6.
12.6. 
 12.8.
12.8. 
 12.10.
12.10. 
 ,
,  , причем
, причем  . Построить график
. Построить график  .
. и
и  с M(X)=2,6. Вычислить среднее квадратическое отклонение
с M(X)=2,6. Вычислить среднее квадратическое отклонение  .
.


 и
и  . Составить закон распределения случайной величины Z=3Y- 2X, и вычислить математическое ожидание М(Z).
. Составить закон распределения случайной величины Z=3Y- 2X, и вычислить математическое ожидание М(Z). и
и  , причем M(X)=1,8. Построить графикF(X) и вычислить среднее квадратическое отклонение
, причем M(X)=1,8. Построить графикF(X) и вычислить среднее квадратическое отклонение 

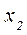 и
и  , дисперсию Х.
, дисперсию Х.

 и
и  , причем M(X)=2,2. Построить графикF(X) и вычислить среднее квадратическое отклонение
, причем M(X)=2,2. Построить графикF(X) и вычислить среднее квадратическое отклонение