 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Нахождение энергетического спектра электрона в яме
Содержание
Задание на курсовую работу
Вариант №4б
Найти энергии и волновые функции первых трех стационарных состояний электрона в потенциальной яме следующего вида:
Построить графики волновых функций этих состояний. Вычислить вероятность обнаружения электрона в центральной части ямы (т.е. в интервале Нахождение энергетического спектра электрона в яме
Потенциальная яма симметрична относительно начала отсчета, следовательно, в дальнейшем можно рассматривать только две области: I - II -
Запишем уравнения Шредингера для областей:
ТУТ ФОРМУЛА
Запишем уравнения в приведенном виде (умножим оба уравнения на
Рассмотрим случай при
« «
Общее решение этих уравнений, с учетом того, что в точке
Граничные условия:
Вследствие симметрии потенциала, решения могут быть четные и нечетные. Рассмотрим оба случая.
1) Четные состояния
Для четных состояний общее решение уравнений Шредингера будет в виде:
Из граничных условий следует:
Разделив одно уравнение на другое получим:
Рассмотрим величину:
Введем новую переменную
где
С учетом этих замен (1) перепишется в виде (умножив обе части уравнения на
Получили трансцендентное уравнение, решение которого можно получить графически (см. рис2).
2) Нечетные состояния
Для нечетных состояний общее решение уравнений Шредингера будет в виде:
Из граничных условий следует:
Разделив одно уравнение на другое получим:
С учетом замен (2) перепишется в виде (умножив обе части уравнения на
Получили трансцендентное уравнение, решение которого можно получить графически (см. рис2).
Рис.2 где
Чтобы избежать комплексных значений
С учетом наложенных ограничений решение трансцендентных уравнений:
Для нахождения
Рассмотрим случай при
« «
Общее решение этих уравнений, с учетом того, что в точке
Граничные условия:
Вследствие симметрии потенциала, решения могут быть четные и нечетные. Рассмотрим оба случая.
3) Четные состояния
Для четных состояний общее решение уравнений Шредингера будет в виде:
Из граничных условий следует:
Разделив одно уравнение на другое получим:
Рассмотрим величину:
Введем новую переменную
где
С учетом этих замен (3) перепишется в виде (умножив обе части уравнения на
Получили трансцендентное уравнение, решение которого можно получить графически (см. рис3).
4) Нечетные состояния
Для четных состояний общее решение уравнений Шредингера будет в виде:
Из граничных условий следует:
Разделив одно уравнение на другое получим:
С учетом замен (4) перепишется в виде (умножив обе части уравнения на
Получили трансцендентное уравнение, решение которого можно получить графически (см. рис3).
Рис.3
где
Чтобы избежать комплексных значений
С учетом наложенных ограничений решение трансцендентных уравнений:
Для нахождения энергетического спектра воспользуемся формулой:
Подставляя полученные значения
Записываю энергии
Допустим, что
|




 , при
, при  ;
; , при
, при  ;
; , при
, при 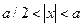 ;
; 




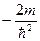 ):
): , где
, где  ;
; , где
, где  ; для
; для 
 , где
, где  ; для
; для 
 функция должна обращаться в 0:
функция должна обращаться в 0:

 ,
, 


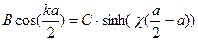


 (1)
(1)
 , тогда:
, тогда: ?,
?, - минимальная энергия частицы.
- минимальная энергия частицы. ):
):







 (2)
(2)






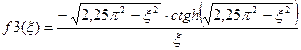
 необходимо наложить ограничение
необходимо наложить ограничение  .
. ;
; ;
; рассмотрим случай с
рассмотрим случай с 




 (3)
(3)
 ,
,


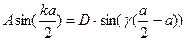

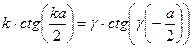
 (4)
(4)
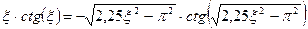

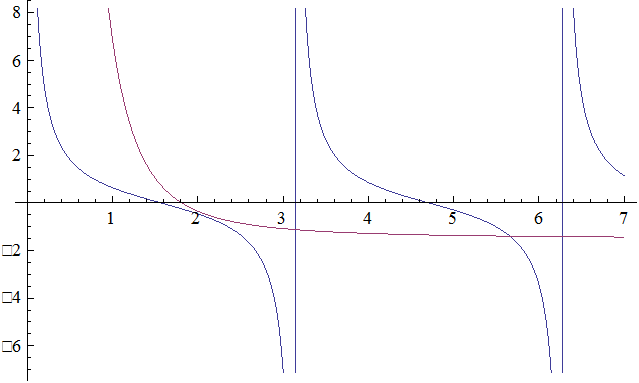

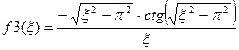
 необходимо наложить ограничение
необходимо наложить ограничение 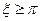
 ;
;

 , получаем:
, получаем: ;
; 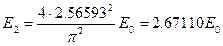 ;
; 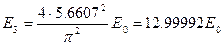 ;
;
 , тогда энергии состояния будут равны:
, тогда энергии состояния будут равны: ;
; ;
; ;
;