ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Задача № 508 Условие задачи
| Плосковыпуклая стеклянная линза с f=1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете r5=1,1 мм. Определить длину световой волны λ. Решение задачи: | 
| Задача № 509 Условие задачи: Между двумя плоскопараллельными пластинами на расстоянии L=10 см от границы их соприкосновения находится проволока диаметром d=0,01 мм, образуя воздушный клин. Пластины освещаются нормально падающим монохроматическим светом (λ=0,6 мкм). Определить ширину b интерференционных полос, наблюдаемых в отраженном свете. | Решение задачи: 
| Задача № 510 Условие задачи: Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (λ=590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d3 воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо. | Решение задачи: 
| Задача № 511 Условие задачи: Какое наименьшее число Nmin штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн λ1=589,0 нм и λ2=589,6 нм? Какова длина l такой решетки, если постоянная решетки d=5 мкм? | Решение задачи: 
| Задача № 512 Условие задачи: На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в n=4,6 раза больше длины световой волны. Найти общее число М дифракционных максимумов, которые теоретически можно наблюдать в данном случае. | Решение задачи: 
| Задача № 513 Условие задачи: На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница (λ=780 нм) спектра третьего порядка? | Решение задачи: 
| Задача № 514 Условие задачи: На дифракционную решетку, содержащую n=600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L=1,2 м. Границы видимого спектра: λкр=780 нм, λф=400 нм. | Решение задачи: 
| Задача № 515 Условие задачи: На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние d между атомными плоскостями равно 280 пм. Под углом θ=65° к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны λ рентгеновского излучения. | Решение задачи: 
| Задача № 516 Условие задачи: На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (λ=600 нм). Угол отклонения лучей, соответствующих второму дифракционному максимуму, φ=20°. Определить ширину a щели. | Решение задачи: 
| Задача № 517 Условие задачи: На дифракционную решетку, содержащую n=100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Δφ=16°. Определить длину волны λ света, падающего на решетку. | Решение задачи: 
| Задача № 518 Условие задачи: На дифракционную решетку падает нормально монохроматический свет (λ=410 нм). Угол Δφ между направлениями на максимумы первого и второго порядков равен 2°21'. Определить число n штрихов на 1 мм дифракционной решетки. | Решение задачи: 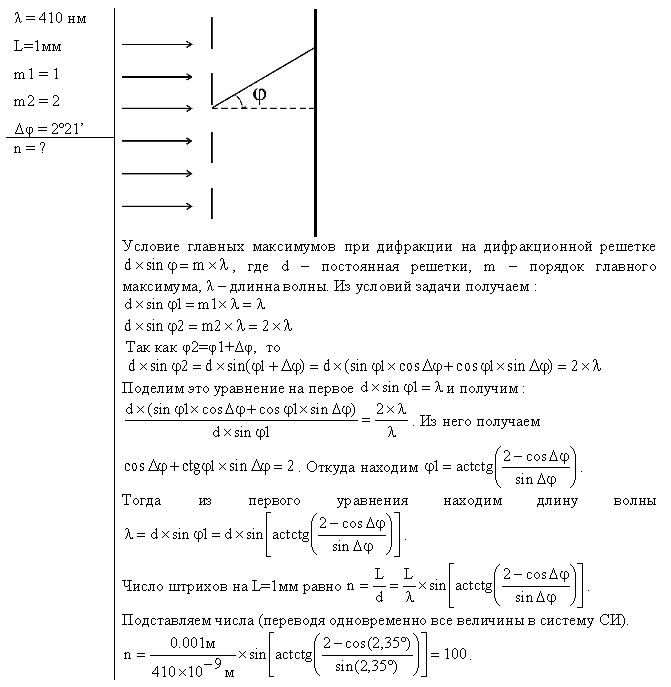
| Задача № 519 Условие задачи: Постоянная дифракционной решетки в n=4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол α между двумя первыми симметричными дифракционными максимумами. | Решение задачи: 
| Задача № 520 Условие задачи: Расстояние между штрихами дифракционной решетки d=4 мкм. На решетку падает нормально свет с длиной волны λ=0,58 мкм. Максимум какого наибольшего порядка дает эта решетка? | Решение задачи: 
| Задача № 521 Условие задачи: Пластинку кварца толщиной d=2 мм поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол φ=53°. Какой наименьшей толщины dmin следует взять пластинку, чтобы поле зрения поляриметра стало совершенно темным? | Решение задачи: 
| Задача № 522 Условие задачи: Параллельный пучок света переходит из глицерина в стекло так, что пучок, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол γ между падающим и преломленным пучками. | Решение задачи: 
| Задача № 523 Условие задачи: Кварцевую пластинку поместили между скрещенными николями. При какой наименьшей толщине dmin кварцевой пластины поле зрения между николями будет максимально просветлено. Постоянная вращения α кварца равна 27 град/мм. | Решение задачи: 
| Задача № 524 Условие задачи: При прохождении света через трубку длиной l1=20 см, содержащую раствор сахара концентрацией C1=10%, плоскость поляризации света повернулась на угол φ1=13,3°. В другом растворе сахара, налитом в трубку длиной l2=15 см, плоскость поляризации повернулась на угол φ2=5,2°. Определить концентрацию C2 второго раствора. | Решение задачи: 
| Задача № 525 Условие задачи: Пучок света последовательно проходит через два николя, плоскости пропускания которых образуют между собой угол φ=40°. Принимая, что коэффициент поглощения k каждого николя равен 0,15, найти, во сколько раз пучок света, выходящий из второго николя, ослаблен по сравнению с пучком, падающим на первый николь. | Решение задачи: 
| Задача № 526 Условие задачи: Угол падения ε луча на поверхность стекла равен 60°. При этом отраженный пучок света оказался максимально поляризованным. Определить угол ε2' преломления луча. | Решение задачи: 
| Задача № 527 Условие задачи: Угол α между плоскостями пропускания поляроидов равен 50°. Естественный свет, проходя через такую систему, ослабляется в n=8 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах. | Решение задачи: 
| Задача № 528 Условие задачи: Пучок света, идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. При каком угле ε падения отраженный пучок света максимально поляризован? | Решение задачи: 
| Задача № 529 Условие задачи: Пучок света переходит из жидкости в стекло. Угол падения ε пучка равен 60°, угол преломления ε2'=50°. При каком угле падения εв пучок света, отраженный от границы раздела этих сред, будет максимально поляризован? | Решение задачи: 
| Задача № 530 Условие задачи: Пучок света падает на плоскопараллельную стеклянную пластину, нижняя поверхность которой находится в воде. При каком угле падения εв свет, отраженный от границы стекло—вода, будет максимально поляризован? | Решение задачи: 
| Задача № 531 Условие задачи: Частица движется со скоростью v=с/3, где с - скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы? | Решение задачи: 
Задача № 532 Условие задачи:Протон с кинетической энергией Т=3 ГэВ при торможении потерял треть этой энергии. Определить, во сколько раз изменился релятивистский импульс α-частицы. Решение задачи:  | Задача № 533 Условие задачи: При какой скорости β (в долях скорости света) релятивистская масса любой частицы вещества в n=3 раза больше массы покоя? | Решение задачи: 
| Задача № 534 Условие задачи: Определить отношение релятивистского импульса p-электрона с кинетической энергией Т=1,53 МэВ к комптоновскому импульсу m0с электрона. | Решение задачи: 
| Задача № 535 Условие задачи: Скорость электрона v=0,8 с (где с — скорость света в вакууме). Зная энергию покоя электрона в мегаэлектрон - вольтах, определить в тех же единицах кинетическую энергию T электрона. | Решение задачи: 
| Задачи № 536 Условие задачи: Протон имеет импульс p=469 МэВ/с. Какую кинетическую энергию необходимо дополнительно сообщить протону, чтобы его релятивистский импульс возрос вдвое? Решение задачи: | 
| Задача № 537 Условие задачи: Во сколько раз релятивистская масса m электрона, обладающего кинетической энергией Т=1,53 МэВ, больше массы покоя m0? | Решение задачи: 
| Задача № 538 Условие задачи: Какую скорость β (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия была равна удвоенной энергии покоя? | Решение задачи: 
| Задача № 539 Условие задачи: Релятивистский электрон имел импульс p1=m0с. Определить конечный импульс этого электрона (в единицах m0c), если его энергия увеличилась в n=2 раза. | Решение задачи: 
| Задача № 540 Условие задачи: Релятивистский протон обладал кинетической энергией, равной энергии покоя. Определить, во сколько раз возрастет его кинетическая энергия, если его импульс увеличится в n=2 раза. | Решение задачи: 
| Задача № 541 Условие задачи: Вычислить истинную температуру Т вольфрамовой раскаленной ленты, если радиационный пирометр показывает температуру Tрад=2,5 кК. Принять, что поглощательная способность для вольфрама не зависит от частоты излучения и равна аi=0,35. | Решение задачи: 
| Задача № 542 Условие задачи: Черное тело имеет температуру Т1=500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в n=5 раз? | Решение задачи: 
| Задача № 543 Условие задачи: Температура абсолютно черного тела Т=2 кК. Определить длину волны λm, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (излучательности) (rλ,T)max для этой длины волны. | Решение задачи: 
| Задача № 544 Условие задачи: Определить температуру Т и энергетическую светимость (излучательность) Re абсолютно черного тела, если максимум энергии излучения приходится на длину волны λm=600 нм. | Решение задачи: 
| Задача № 545 Условие задачи: Из смотрового окошечка печи излучается поток Фe=4 кДж/мин. Определить температуру Т печи, если площадь окошечка S=8 см2. | Решение задачи: 
| Задача № 546 Условие задачи: Поток излучения абсолютно черного тела Фe=10 кВт. Максимум энергии излучения приходится на длину волны λm=0,8 мкм. Определить площадь S излучающей поверхности. | Решение задачи: 
| Задача № 547 Условие задачи: Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (λm1=780 нм) на фиолетовую (λm2=390 нм)? | Решение задачи: 
| Задача № 548 Условие задачи: Определить поглощательную способность aT серого тела, для которого температура, измеренная радиационным пирометром, Tрад=1,4 кК, тогда как истинная температура Т тела равна 3,2 кК. | Решение задачи: 
| Задача № 549 Условие задачи: Муфельная печь, потребляющая мощность Р=1 кВт, имеет отверстие площадью S=100 см2. Определить долю η мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна 1 кК. | Решение задачи: 
| Задача № 550 Условие задачи: Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см2*мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты aT=0,25? | Решение задачи: 
| Задача № 551 Условие задачи: Красная граница фотоэффекта для цинка λ0=310 нм. Определить максимальную кинетическую энергию Tmax фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны λ=200 нм. | Решение задачи: 
| Задача № 552 Условие задачи: На поверхность калия падает свет с длиной волны λ=150 нм. Определить максимальную кинетическую энергию Tmax фотоэлектронов. | Решение задачи: 
| Задача № 553 Условие задачи: Фотон с энергией ε=10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс p, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластины. | Решение задачи: 
| Задача № 554 Условие задачи: На фотоэлемент с катодом из лития падает свет с длиной волны λ=200 нм. Найти наименьшее значение задерживающей разности потенциалов Umin, которую нужно приложить к фотоэлементу, чтобы прекратить фототок. | Решение задачи: 
| Задача № 555 Условие задачи: Какова должна быть длина волны γ-излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была vmax=3 Мм/с? | Решение задачи: 
| Задача № 556 Условие задачи: На металлическую пластину направлен пучок ультрафиолетового излучения (λ=0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов Umin=0,96 В. Определить работу выхода А электронов из металла. | Решение задачи: 
| Задача № 557 Условие задачи: На поверхность металла падает монохроматический свет с длиной волны λ=0,1 мкм. Красная граница фотоэффекта λ0=0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? | Решение задачи: 
| Задача № 558 Условие задачи: На металл падает рентгеновское излучение с длиной волны λ=1 нм. Пренебрегая работой выхода, определить максимальную скорость vmax фотоэлектронов. | Решение задачи: 
| Задача № 559 Условие задачи: На металлическую пластину направлен монохроматический пучок света с частотой ν=7,3*1014 Гц. Красная граница λ0 фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость vmax фотоэлектронов. | 
| Задача № 560 Условие задачи: На цинковую пластину направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов U=1,5 В. Определить длину волны λ света, падающего на пластину. | Решение задачи: 
| Задача № 561 Условие задачи: Фотон при эффекте Комптона на свободном электроне был рассеян на угол ϑ=π/2. Определить импульс p (в МэВ/с), приобретенный электроном, если энергия фотона до рассеяния была ε1=1,02 МэВ. | Решение задачи: 
| Задача № 562 Условие задачи: Рентгеновское излучение (λ=1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны λmax рентгеновского излучения в рассеянном пучке. | Решение задачи: 
| Задача № 563 Условие задачи:Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол ϑ=π/2? Энергия фотона до рассеяния ε1=0,51 МэВ. Решение задачи: | 
| Задача № 564 Условие задачи: Определить максимальное изменение длины волны (Δλ)max при комптоновском рассеянии света на свободных электронах и свободных протонах. | Решение задачи: 
| Задача № 565 Условие задачи: Фотон с длиной волны λ1=15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона λ2=16 пм. Определить угол ϑ рассеяния. | Решение задачи: 
| Задача № 566 Условие задачи:Фотон с энергией ε1=0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол ϑ=180°. Определить кинетическую энергию T электрона отдачи. Решение задачи: | 
| Задача № 567 Условие задачи: В результате эффекта Комптона фотон с энергией ε1=1,02 МэВ рассеян на свободных электронах на угол ϑ=150°. Определить энергию ε2 рассеянного фотона. | Решение задачи: 
| Задача № 568 Условие задачи: Определить угол ϑ, на который был рассеян квант с энергией ε1=1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи T=0,51 МэВ. | Решение задачи: 
| Задача № 569 Условие задачи: Фотон с энергией ε1=0,51 МэВ при рассеянии на свободном электроне потерял половину своей энергии. Определить угол рассеяния ϑ. | Решение задачи: 
| Задача № 570 Условие задачи: Определить импульс pe электрона отдачи, если фотон с энергией ε1=1,53 МэВ в результате рассеяния на свободном электроне потерял 1/3 своей энергии. Решение задачи: | 
| Задача № 571 Условие задачи: Определить энергетическую освещенность (облученность) Ee зеркальной поверхности, если давление p, производимое излучением, равно 40 мкПа. Излучение падает нормально к поверхности. | Решение задачи: 
| Задача № 572 Условие задачи: Давление p света с длиной волны λ=40 нм, падающего нормально на черную поверхность, равно 2 нПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности. | Решение задачи: 
| Задача № 573 Условие задачи: Определить коэффициент отражения ρ поверхности, если при энергетической освещенности Еe=120 Вт/м2 давление p света на нее оказалось равным 0,5 мкПа. | Решение задачи: 
| Задача № 574 Условие задачи: Давление света, производимое на зеркальную поверхность, p=5 мПа. Определить концентрацию n0 фотонов вблизи поверхности, если длина волны света, падающего на поверхность, λ=0,5 мкм. | Решение задачи: 
| Задача № 575 Условие задачи: На расстоянии r=5 м от точечного монохроматического (λ=0,5 мкм) изотропного источника расположена площадка (S=8 мм2) перпендикулярно падающим пучкам. Определить число N фотонов, ежесекундно падающих на площадку. Мощность излучения Р=100 Вт. | Решение задачи: 
| Задача № 576 Условие задачи: На зеркальную поверхность под углом α=60° к нормали падает пучок монохроматического света (λ=590 нм). Плотность потока энергии светового пучка φ=1 кВт/м2. Определить давление p, производимое светом на зеркальную поверхность. | Решение задачи: 
| Задача № 577 Условие задачи: Свет падает нормально на зеркальную поверхность, находящуюся на расстоянии r=10 см от точечного изотропного излучателя. При какой мощности Р излучателя давление р на зеркальную поверхность будет равным 1 мПа? | Решение задачи: 
| Задача № 578 Условие задачи: Свет с длиной волны λ=600 нм нормально падает на зеркальную поверхность и производит на нее давление p=4 мкПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности. | Решение задачи: 
| Задача № 579 Условие задачи: На зеркальную поверхность площадью S=6 см2 падает нормально поток излучения Фe=0,8 Вт. Определить давление p и силу давления F света на эту поверхность. | Решение задачи: 
| Задача № 580 Условие задачи: Точечный источник монохроматического (λ=1 нм) излучения находится в центре сферической зачерненной колбы радиусом R=10 см. Определить световое давление p, производимое на внутреннюю поверхность колбы, если мощность источника P=1 кВт. | Решение задачи: 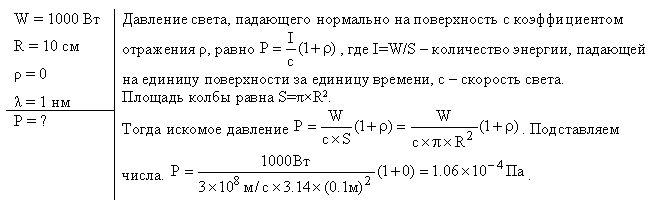
|