ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Исследование устойчивости САУ в среде пакета MATLAB-Simulink.
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ ПО ДИСЦИПЛИНЕ " ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ " ТЕМА " ИССЛЕДОВАНИЕ ЛИНЕЙНЫХ САУ"
Специальность - 140604 " Электропривод и автоматика промышленных установок и технологических Студент гр. 3ЭП-31 Бида Петр Ильич фамилия, имя, отчество
Дата_____________ Подпись студента_________________
Допустить к защите:________________( Н.В.Кочнев)
Защита работы состоится ______
Дата защиты ________ Оценка _______________
Председатель комиссии______________(Н.В.Кочнев)
Череповец, 2013 Содержание
Введение. 2 Исходные данные. 3 Исследование устойчивости САУ в среде пакета Mathcad. 3 Исследование устойчивости САУ в среде пакета MATLAB-Simulink. 9 Анализ результатов. 18 Заключение. 19 Литература. 20
Введение
Целью данной курсовой работы является исследование устойчивости линейной САУ различными методами анализа (частотными и алгебраическими) с применением двух программных пакетов Mathcad и Matlab-Simulink. На основе произведенных исследований сделать выводы об устойчивости системы и о совпадении результатов, полученных в обоих программных продуктах.
Вариант 2: Структурная схема:
Коэффициенты усиления: К1 = 10, К2 = 5, К3 = 4 Постоянные времени (с): Т1 = 0,5; Т2 = 0,25; Т3 = 0,1; Т4 = 0,05 Исследование устойчивости САУ в среде пакета Mathcad.
Найдём передаточную функцию системы Элементы W1 и W2 имеют обратную связь. Их передаточная функция запишется в виде:
Элементы W12 и W3 соединены последовательно.Их передаточная функция запишется в виде:
Далее элементы W1 и W2 соединены параллельно. Их передаточная функция запишется в виде:
Элементы W123 и W4 имеют обратную связь. Их передаточная функция запишется в виде:
Упростим данную функцию в системе Mathcad, и, подставим численные значения:
Заменим оператор p(S) на iw:
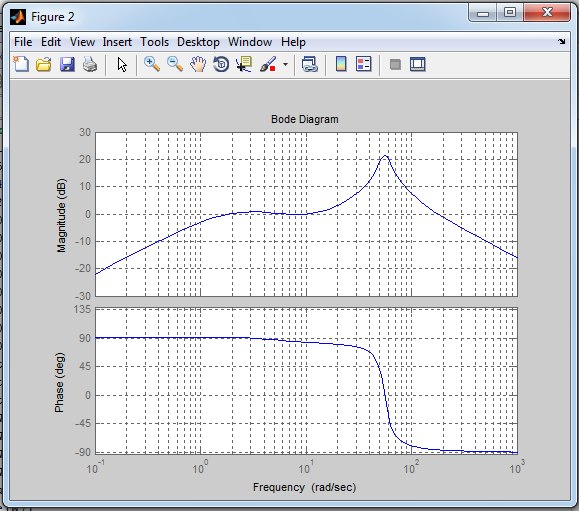
АФЧХ (годограф) передаточной функции будет иметь вид:
Логарифмическая характеристика строится на основе формулы:
Частота изменяется в пределах:
Фазовая характеристика строится на основе формулы:
Исследуем устойчивость системы с помощью критерия Михайлова.
По критерию Михайлова система устойчива, если годограф, начинаясь при ω=0 на положительной действительной полуоси, огибает с ростом частоты от 0 до
По виду годографа можно сказать, что система неустойчива.
Исследуем устойчивость системы с помощью критерия Гурвица.
По этому критерию система является устойчивой, если все определители матрицы Гурвица положительны.
В нашем же случае все определители отрицательны, отсюда вывод – система неустойчива.
Исследование устойчивости САУ в среде пакета MATLAB-Simulink.
Структурная схема САУ имеет вид:
Ниже представлен график переходного процесса.
По колебаниям графика годографа видно, что с ростом времени колебания увеличиваются – система неустойчива.
Скрипт для исследования устойчивости САУ в среде пакета Matlab-Simulink имеет вид:
K1=10; K2=5; K3=4; K4=2; K5=0.5; T1=0.5; T2=0.25; T3=0.1; T4=0.05; T5=0.3; T6=0.6; T7=0.1; W1=tf([K1],[T1 1]); W2=tf([K2],[1 0]); W3=tf([K3*T3 K3*1],[T4 1]); W4=W1/(1+W1*W2); W5=W4*W3; W6=W1/(1-W1*W2); W7=W5/(1+W5*W6); figure step(W7) grid on
Изменяя step(W7) на impulse, nyquist, bode получали различные графики с осциллографов.
STEP - график переходного процесса (зависимость амплитуды сигнала от времени):
IMPULSE:
АФЧХ (годограф):
По виду годографа можно заключить, что система неустойчива, так как он охватывает точку (-1;j0).
Ниже представлены ЛАЧХ и ФЧХ, BODE:
Нахождение корней характеристического полинома (знаменатель) и полинома в числителе с помощью Mathlab, команды pole и zero. Корни:
ans =
-6.8851 +55.6653i
ans = 0
Среди полученных корней некоторые имеют положительную вещественную часть, что говорит о неустойчивости системы.
Анализ результатов.
В ходе работы было проведено исследование САУ различными методами в различных программных пакетах. В ходе исследования в пакете Mathcad неустойчивость системы показали все 3 критерия: критерий Михайлова, Гурвица, Найквиста. В пакете MatLab также все исследования показали неустойчивость системы: по критерию Найквиста САУ неустойчива, осциллограф колебаний системы говорит о том же, да и корневой метод даёт неустойчивость (среди 16 корней все корни 2 корня неустойчивы). На основе проведённых исследований можно сделать вывод о том, что система неустойчива. Повысить устойчивость САУ можно эффективным средством стабилизации неустойчивого объекта - охватом его отрицательной обратной связью и использование регуляторов с передаточными функциями, содержащими форсирующие множители. Передаточные функции ПИ-, ПИД- и ПД-регуляторов, а также инерционно-форсирующие звенья содержат форсирующие множители, обеспечивающие стабилизацию.
Заключение.
В данной работе был проведён анализ устойчивости линейной САУ. Использовались математические пакеты MathCad и Matlab-Simulink. Методы корневого годографа, Гурвица, Михайлова, частотных характеристик показали, что система неустойчива. Различие некоторых графиков математических пакетов MathCad и Matlab-Simulink можно объяснить допущенными упрощениями, которые мы выполняли в ходе работы.
Литература
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. - Профессия – 2003 – 752с. 2. Теория управления - 1 - Теория линейных САУ - УП - Туманов - 2005 – 82. |



 комплексов"
комплексов"

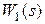






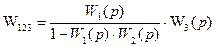







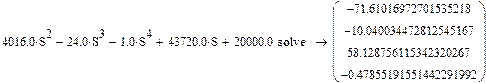





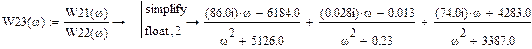

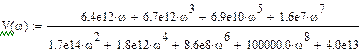










 против часовой стрелки начало координат, проходя последовательно в положительном направлении n квадрантов.
против часовой стрелки начало координат, проходя последовательно в положительном направлении n квадрантов.