 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Унарные операции над множествами
Реферат тема: «алгебраические операции над множителями»
Выполнила:
Алексеевка 2013г Содержание Введение. 3 1.История теории множеств. 4 2. Операции над множествами. 6 2.1 Сравнение множеств. 6 2.2 Бинарные операции. 7 2.3 Диаграммы Эйлера — Венна. 8 2.4 Унарные операции над множествами. 11 Приоритет выполнения операций. 12
Мно́жество — одно из ключевых понятий математики, в частности, теории множеств и логики. Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит, и не имеющее определения. Однако, можно дать описание множества, например, в формулировке Георга Кантора: Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M). Другая формулировка принадлежит Бертрану Расселлу: «Множество есть совокупность различных элементов, мыслимая как единое целое». Также возможно косвенное определение через аксиомы теории множеств. В математической логике и дискретной математике часто употребляемый синоним множества — алфавит. Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.
История теории множеств До XIX века математиками рассматривались в основном конечные множества. Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов. С 1872 г. по 1897 г. (главным образом в 1872—1884 гг.) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности Георг Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал элементами множества. Множество объектов, обладающих свойством , обозначил . Если некоторое множество , то назвал характеристическим свойством множества . Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 г. теория множеств была аксиоматизирована независимо Бертраном Расселем и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. В настоящее время, теорию множеств Кантора принято называть наивной теорией множеств, а вновь построенную аксиоматической теорией множеств. На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков). Операции над множествами
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые.
Сравнение множеств
Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:
Бинарные операции Ниже перечислены основные операции над множествами:
· Объединение
· Разность (дополнение)
· Симметрическая разность:
· Декартово или прямое произведение
Диаграммы Эйлера — Венна
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек. Диаграмма Эйлера-Венна - наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Количество пересечений (областей) n определяется по формуле: n=2N, где N - количество множеств. Таким образом, если в задаче используется два множества, то n=22=4, если три множества, то n=23=8, если четыре множества, то n=24=16. Поэтому диаграммы Эйлера-Венна используются в основном для двух или трех множеств. Множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 множества), помещенных в прямоугольник (универсум). Универсальное множество (универсум) U (в контексте задачи) - множество, содержащее все элементы рассматриваемой задачи: элементы всех множеств задачи и элементы, не входящие в них. Пустое множество Ø (в контексте задачи) - множество, не содержащее ни одного элемента рассматриваемой задачи. На диаграмме строят пересекающиеся множества, заключают их в универсум. Выделяют области, количество которых равно количеству пересеений. Диаграммы Эйлера-Венна также используются для визуального представления логических операций. Разберем примеры построения диаграмм Эйлера-Венна для двух и трех множеств. Пример 1 Пусть есть следующие множества чисел: А={1,2,3,4} В={3,4,5,6} Универсум U={0,1,2,3,4,5,6}
Диаграммы Эйлера-Венна для двух множеств А и В:
Рисунок 1 Диаграммы Эйлера-Венна для двух множеств А и В
Определим области, и числа которые им принадлежат: Определим области, и числа которые им принадлежат: А B Обозначение области Числа 0 0 0) 0 0 1 1) 5,6 1 0 2) 1,2 1 1 3) 3,4
Пример 2 Пусть есть следующие множества чисел: А={1,2,3,4} В={3,4,5,6} С={1,3,6,7} Универсум U={0,1,2,3,4,5,6,7} Диаграммы Эйлера-Венна для трех множеств А, В, С:
Рисунок 2 Диаграммы Эйлера-Венна для двух множеств А и В
Определим области, и числа которые им принадлежат :А B C Обозначение области Числа 0 0 0 0) 0 0 0 1 1) 7 0 1 0 2) 5 0 1 1 3) 6 1 0 0 4) 2 1 0 1 5) 1 1 1 0 6) 4 1 1 1 7) 3 Унарные операции над множествами
Операция дополнения подразумевает некоторый универсум (универсальное множество U, которое содержит )A:
Относительным же дополнением называется А\В (см.выше): Мощность множества:
Результатом является кардинальное число (для конечных множеств — натуральное). Множество всех подмножеств (булеан):
Обозначение происходит из того, что в случае конечных множеств. |
Множество А содержится во множестве В (множество В включает множество А), если каждый элемент А есть элемент В:
В этом случае А называется подмножеством В, В— надмножеством А. Если
А В и А=B, то А называется собственным подмножеством В. Заметим, что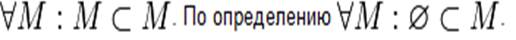
.
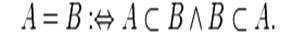Два множества называются равными, если они являются подмножествами друг друга:
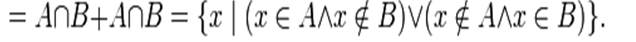
Абсолютное дополнение:
