 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Оценка точности прогноза, построенного методом экстраполяции
Слайд. Эмпирической мерой точности прогноза, служит величина его ошибки, которая определяется как разность между прогнозными ( Данный подход возможен только в двух случаях: а) период упреждения известен, уже закончился, и исследователь располагает необходимыми фактическими значениями прогнозируемого показателя; б) строится ретроспективный прогноз, то есть рассчитываются прогнозные значения показателя для периода времени, за который уже имеются фактические значения. Это делается с целью проверки разработанной методики прогнозирования. В данном случае вся имеющаяся информация делится на две части в соотношении 2/3 к 1/3. Одна часть информации (первые 2/3 от исходного временного ряда) служит для оценивания параметров модели прогноза. Вторая часть информации (последняя 1/3 части исходного ряда) служит для реализации оценок прогноза. Полученные таким образом ретроспективно ошибки прогноза в некоторой степени характеризуют точность предлагаемой и реализуемой методики прогнозирования. Однако величина ошибки ретроспективного прогноза не может в полной мере и окончательно характеризовать используемый метод прогнозирования, так как она рассчитана только для 2/3 имеющихся данных, а не по всему временному ряду. В случае если, ретроспективное прогнозирование осуществляется по связным и многомерным динамическим рядам, то точность прогноза, соответственно, будет зависеть от точности определения значений факторных признаков, включенных в многофакторную динамическую модель, на всем периоде упреждения. При этом, возможны следующие подходы к прогнозированию по связным временным рядам: можно использовать как фактические, так и прогнозные значения признаков. 4 слайд Все показатели оценки точности статистических прогнозов условно можно разделить на три группы: – аналитические; – сравнительные; – качественные. 5 слайд Аналитические показатели точности прогнозапозволяют количественно определить величину ошибки прогноза. К ним относятся: 6 слайд Абсолютная ошибка прогноза (D*) определяется как разность между эмпирическими и прогнозными значениями признака и вычисляется по формуле:
где: уt–фактическое значение признака;
7 слайд Относительная ошибка прогноза (d*отн) может быть определена как отношение абсолютной ошибки прогноза (D*):
— к фактическому значению признака (уt):
— к прогнозному значению признака (
8 слйд Абсолютная и относительная ошибки прогноза являются оценкой проверки точности единичного прогноза, что снижает их значимость в оценке точности всей прогнозной модели, так как изучаемое социально-экономическое явление подвержено влиянию различных факторов внешнего и внутреннего свойства. Единично удовлетворительный прогноз может быть получен и на базе реализации слабо обусловленной и недостаточно адекватной прогнозной модели и наоборот – можно получить большую ошибку прогноза по достаточно хорошо аппроксимирующей модели. Слайд Поэтому на практике иногда определяют не ошибку прогноза, а некоторый коэффициент качества прогноза (Кк), который показывает соотношение между числом совпавших (с) и общим числом совпавших (с) и несовпавших (н) прогнозов и определяется по формуле:
Слайд Значение Кк = 1 означает, что имеет место полное совпадение значений прогнозных и фактических значений и модель на 100% описывает изучаемое явление. Данный показатель оценивает удовлетворительный вес совпавших прогнозных значений в целом по временному ряду и изменяется в пределах от 0 до 1. Следовательно, оценку точности получаемых прогнозных моделей целесообразно проводить по совокупности сопоставлений прогнозных и фактических значений изучаемых признаков. 11 слайд Средним показателем точности прогнозаявляется средняя абсолютная ошибка прогноза (
Слайд где: n–длина временного ряда. Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака. Слайд Для оценки точности прогноза используется средняя квадратическая ошибка прогноза, определяемая по формуле:
Слайд Размерность средней квадратической ошибки прогноза также соответствует размерности изучаемого признака. Между средней абсолютной и средней квадратической ошибками прогноза существует следующее примерное соотношение:
Лайд Недостатками средней абсолютной и средней квадратической ошибок прогноза является их существенная зависимость от масштаба измерения уровней изучаемых социально-экономических явлений. Поэтому на практике в качестве характеристики точности прогноза определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле вида:
Данный показатель является относительным показателем точности прогноза и не отражает размерность изучаемых признаков, выражается в процентах и на практике используется для сравнения точности прогнозов полученных как по различным моделям, так и по различным объектам Слайд В качествесравнительного показателя точности прогнозаиспользуетсякоэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:
Слайд где:
Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака. Слайд Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться в различных модификациях: 1. Коэффициент несоответствия (КН1), определяемый как отношение средней квадратической ошибки к квадрату фактических значений признака: Слайд
КН = 0, если Слайд КН = 1, если при прогнозировании получают среднюю квадратическую ошибку адекватную по величине ошибке, полученной одним из простейших методов экстраполяции неизменности абсолютных цепных приростов. КН > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент несоответствия не имеет. Слайд 2.Коэффициент несоответствия (КН2), определяется как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от среднего уровня исходного временного ряда за весь рассматриваемый период:
где:
Слайд 3.Коэффициент несоответствия (КН3), определяемый как отношение средней квадратической ошибки прогноза к сумме квадратов отклонений фактических значений признака от теоретических, выравненных по уравнению тренда:
где:
Слайд Оценка точности прогноза, построенного методом экстраполяции Всякий прогноз должен иметь высокую точность, которая является важнейшей его характеристикой. Существует несколько способов оценки точности прогноза: 1. Cредняя абсолютная оценка:
где Yф – фактическое значение исследуемого явления, Yр – расчетное значение исследуемого явления, n – число уровней временного ряда; 2. Cредняяквадратическая оценка:
Чем ближе к нулю первый и второй показатели, тем выше точность прогноза. Слайд 3. Cредняя относительная ошибка: Слайд Верификация. Прямая верификация – требует подтверждения сделанного прогноза любыми другим альтернативными методами прогнозирования, отличными от того, который использовался по факту прогнозистом. Косвенная верификация – предполагается подтверждение прогнозной информации из любых других источников информации, касающихся данного объекта. Инверсная верификация – осуществляется проверка прогностической пригодности метода либо модели на ретроспективном периоде прогнозирования. Консеквентная верификация – определяется как получение значений верифицируемого прогноза путем неких логических либо аналитических выводов из ранее уже сделанных успешных прогнозов. Дублирующая верификация (проверка повторным опросом) – предполагает сравнение исходных результатов прогноза со значениями другого предсказания, полученного при иной формулировке постановки исходного вопроса, проблемы. Оппонентная верификация – осуществляется путем успешного опровержения критических замечаний со стороны внешних заинтересованных субъектов касательно итога либо методики проведения прогноза. Верификация путем снижения систематических ошибок – прогнозисту надлежит выявить и минимизировать источники регулярных ошибок прогноза. Верификация экспертом – предполагается сравнение результата прогнозирования с мнением наиболее компетентного в данной предметной области эксперта. Слайд 3 способа оценки точности прогноза и выбора оптимальной модели Существует множество моделей прогноза, но как выбрать среди них ту, которая наиболее точно сделает прогноз? Какие способы оценки прогнозной модели вы можете использовать: 1. Оценить отношение фактических продаж к прогнозу; 2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные; 3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;
Слайд 1-й способ — Расчет отношения фактических продаж к прогнозу. Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач.Если задача - сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).
Слайд Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:
· Линейный тренд + сезонность · Логарифмический тренд + сезонность · Скользящая средняя с сезонностью к 2-м месяцам · Скользящяясредняя с сезонностью к 3-м месяцам
Для каждой из 4-х прогнозных моделей : 29 слайд · Суммируем прогноз по каждой модели за 6 месяцев;
30 слайд · Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;
31 слайд · Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;
32 слайд · Рассчитываем по каждой модели среднее отношение факта к прогнозу;
33 слайд · Выбираем модель прогноза, которая по показателю "среднее отношение факта к прогнозу" оказалась максимально приближена к 100%
Слайд Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.
Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от фактических продаж. Слайд 2-й способ оценки модели прогноза — расчет показателя точность прогноза. Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз. Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью. Слайд · Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом
Слайд · Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.
Слайд · Рассчитываем квадратическое отклонение ошибки от значений прогнозной
Слайд · Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение
Слайд · Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100
Слайд Показатель точности прогноза выражается в процентах: · Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно. · Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит. Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда. Слайд 3. Способ оценки прогнозной модели — визуальный. На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике. Слайд Линейная модель:
Слайд Логарифмическая модель:
По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз. Слайд Какую модель прогноза выбрать?
· Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%. · Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически). · Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.
|
) и фактическими (уt) значениями исследуемого показателя. 3 слайд
, (3.54)
(3.55)
)
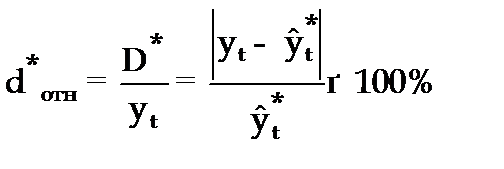(3.56)
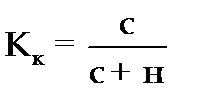. (3.57)
), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:
, (3.58)
. (3.59)
. (3.60)
. (3.61)
, (3.62)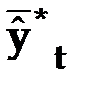
– средний уровень ряда динамики прогнозных оценок.
. (3.63)
, то есть полное совпадение фактических и прогнозных значений признака.
, (3.64)
–средний уровень исходного ряда динамики.
, (3.65)
–теоретические уровни временного ряда, полученные по модели тренда.
